貝葉斯機器學習——探索統計數據建模的範式轉變
已發表: 2020-11-24目錄
什麼是貝葉斯機器學習？
貝葉斯機器學習（也稱為貝葉斯機器學習）是一種基於貝葉斯定理構建統計模型的系統方法。
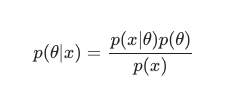任何標準的機器學習問題都包括兩個需要分析的主要數據集：
- 一套全面的訓練數據
- 所有可用輸入和所有記錄輸出的集合
分析這些數據以進行建模的傳統方法是確定可以在這些數據集之間映射的一些模式。 分析師通常會將模型拼接在一起以確定這些模型之間的映射，由此產生的方法是一種非常確定的方法來生成目標變量的預測。
唯一的問題是，絕對沒有辦法用一套清晰的定義來解釋這個模型內部發生的事情。 本質上，所完成的只是最小化訓練數據集上的一些損失函數——但這幾乎不能算作真正的建模。
一個理想的（最好是無損的）模型需要對模型的固有參數進行客觀總結，並輔以可以用數學概率語言定義和維護的統計彩蛋（例如置信區間）。 這種“理想”的場景是貝葉斯機器學習想要完成的。
貝葉斯機器學習的目標（和魔法）
貝葉斯機器學習的主要目標是估計後驗分佈，給定可能性（訓練數據的導數估計）和先驗分佈。
在訓練常規機器學習模型時，這正是我們最終在理論和實踐中所做的事情。 眾所周知，分析師會對訓練數據執行最大似然估計的連續迭代，從而以最大化看到它導致了一個先有雞還是先有蛋的問題，貝葉斯機器學習旨在完美地解決這個問題。
假設訓練數據是固定的，從而確定伴隨所述數據的任何參數設置的概率，分析師尋求這個過程稱為Maximum A Postiori ，簡稱為MAP 。 掌握這個概念的一個更簡單的方法是根據似然函數來考慮它。
考慮到貝葉斯定理，後驗可以定義為：
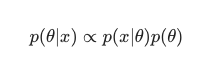
在這種情況下，我們將分母作為一種簡單的反冗餘措施排除在外。 在最大化過程中可以忽略任何不會導致對模型的依賴。 這個難題的關鍵部分，即先驗分佈，是讓貝葉斯模型與經典的 MLE 訓練模型相比脫穎而出的原因。
分析師通常可以對特定參數配置的適合程度做出合理的假設，這對編碼他們對這些參數的看法大有幫助，甚至在他們實時看到這些參數之前。 例如，在模型參數上使用高斯先驗是相對常見的。
這裡的分析師假設這些參數是從正態分佈中提取的，其中顯示了均值和方差。 這種分佈具有經典的鐘形曲線形狀，鞏固了其質量的很大一部分，令人印象深刻地接近平均值。
另一方面，尾部值的出現非常罕見。 使用這樣的先驗，有效地表明了這樣一種信念，即模型的大多數權重必須符合定義的狹窄範圍，非常接近平均值，只有少數異常值。 考慮到現實世界的現象和非理想情況，這是一個合理的信念。
然而，當您觀察到使用這些先驗分佈（和MAP過程）產生的結果驚人地相似時，貝葉斯模型的效果會更加有趣，如果不等於通過執行經典意義上的 MLE 解決的結果，輔助一些額外的正則化。
有趣的是，僅通過使用先驗約束“接受的”模型權重，我們最終創建了一個正則化器。
總體而言，貝葉斯機器學習作為機器學習的一個子領域正在迅速發展，進一步發展和進入既定標準似乎是當前計算和統計硬件進步步伐的一個相當自然和可能的結果。
閱讀：貝葉斯網絡
貝葉斯機器學習的不同方法
貝葉斯機器學習有三種被廣泛接受的方法，即MAP 、MCMC 和“高斯”過程。
使用 MAP的貝葉斯機器學習：最大後驗概率
MAP享有作為邁向真正貝葉斯機器學習的第一步的區別。 然而，它在計算像點估計這樣基本的東西的能力上是有限的，正如經驗豐富的統計學家通常所說的那樣。
點估計的問題在於，除了最佳設置之外，它們並沒有透露太多關於參數的信息。 分析師和統計學家經常追求額外的、核心有價值的信息，例如，某個參數值落在這個預定義範圍內的概率。 畢竟，這就是貝葉斯機器學習的真正預測能力所在。
使用 MCMC 進行貝葉斯機器學習：馬爾可夫鏈蒙特卡羅
馬爾可夫鏈蒙特卡羅，也通常稱為 MCMC，是一種流行且著名的“繖形”算法，通過一組著名的輔助方法如 Gibbs 和 Slice Sampling 應用。
雖然 MCMC 的數學通常被認為是困難的，但它仍然同樣有趣和令人印象深刻。 這些輔助方法的高潮是構建一個已知的馬爾可夫鏈，進一步確定一個與後驗等效的分佈。
許多連續的算法選擇通過包含梯度信息來改進 MCMC 方法，以試圖讓分析人員以更高的效率導航參數空間。
然而，有更簡單的方法可以實現這種準確性。 例如，有貝葉斯線性和邏輯回歸等價物，其中分析師使用拉普拉斯近似。 後驗分佈的解析近似（可以在紙上解釋）是這個過程與眾不同的地方。
必讀：樸素貝葉斯解釋
使用高斯過程的貝葉斯機器學習
高斯過程是一個隨機過程，對所有組成隨機變量施加嚴格的高斯條件。 它們的工作原理是確定所有可能線空間上的概率分佈，然後在考慮數據的情況下選擇最有可能成為實際預測變量的線。
這些過程最終允許分析師在功能空間中執行回歸。 鑑於整個後驗分佈是在這種方法中進行分析計算的，這無疑是最真實的貝葉斯估計，因此在統計上和邏輯上都是最令人欽佩的。
如果您想了解更多關於機器學習和人工智能職業的信息，請查看 IIT Madras 和 upGrad 的機器學習和雲高級認證。