Învățare automată bayesiană – Explorarea unei schimbări de paradigmă în modelarea datelor statistice
Publicat: 2020-11-24Cuprins
Ce este Bayesian Machine Learning?
Învățarea automată bayesiană (cunoscută și sub numele de Bayesian ML) este o abordare sistematică pentru construirea de modele statistice, bazată pe teorema lui Bayes.
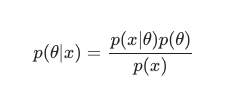Orice problemă standard de învățare automată include două seturi de date principale care necesită analiză:
- Un set cuprinzător de date de antrenament
- O colecție de toate intrările disponibile și toate ieșirile înregistrate
Abordarea tradițională a analizei acestor date pentru modelare este de a determina unele modele care pot fi mapate între aceste seturi de date. De obicei, un analist va îmbina un model pentru a determina maparea dintre acestea, iar abordarea rezultată este o metodă foarte deterministă pentru a genera predicții pentru o variabilă țintă.
Singura problemă este că nu există absolut nicio modalitate de a explica ceea ce se întâmplă în interiorul acestui model cu un set clar de definiții. Tot ceea ce se realizează, în esență, este reducerea la minimum a unor funcții de pierdere din setul de date de antrenament - dar asta cu greu se califică drept modelare adevărată .
Un model ideal (și, de preferință, fără pierderi) presupune un rezumat obiectiv al parametrilor inerenți ai modelului, completat cu ouă de Paște statistice (cum ar fi intervalele de încredere) care pot fi definite și apărate în limbajul probabilității matematice. Acest scenariu „ideal” este ceea ce Bayesian Machine Learning își propune să realizeze.
Obiectivele (și magia) ale învățării automate bayesiene
Obiectivul principal al Bayesian Machine Learning este de a estima distribuția posterioară , având în vedere probabilitatea (o estimare derivată a datelor de antrenament) și distribuția anterioară .
Când antrenăm un model obișnuit de învățare automată, asta este exact ceea ce ajungem să facem în teorie și practică. Se știe că analiștii efectuează iterații succesive ale estimării probabilității maxime pe datele de antrenament, actualizând astfel parametrii modelului într-un mod care maximizează probabilitatea de a vedea Aceasta duce la o problemă de găină și ou, pe care Bayesian Machine Learning își propune să o rezolve frumos.
Lucrurile iau o cu totul altă întorsătură într-o situație dată în care un analist încearcă să maximizeze distribuția posterioară , presupunând că datele de antrenament vor fi fixate și, prin urmare, determinând probabilitatea oricărei setari de parametri care însoțește datele respective. Acest proces se numește Maximum A Posterior , prescurtat ca MAP . O modalitate mai ușoară de a înțelege acest concept este să ne gândim la el în termeni de funcție de probabilitate .
Luând în considerare teorema lui Bayes , posteriorul poate fi definit ca:
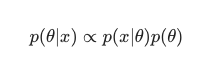
În acest scenariu, omitem numitorul ca o simplă măsură anti-redundanță. Orice lucru care nu provoacă dependență de model poate fi ignorat în procedura de maximizare. Această piesă cheie a puzzle-ului, distribuția anterioară, este cea care permite modelelor bayesiene să iasă în evidență în contrast cu omologii lor clasici instruiți în MLE.
Analiștii pot face adesea presupuneri rezonabile cu privire la cât de potrivită este o anumită configurație a unui parametru, iar acest lucru ajută la codificarea convingerilor lor despre acești parametri chiar înainte de a-i vedea în timp real. Este relativ obișnuit, de exemplu, să folosiți un antecedent gaussian peste parametrii modelului.
Analistul de aici presupune că acești parametri au fost extrași dintr-o distribuție normală, cu o anumită afișare atât a mediei, cât și a varianței. Acest tip de distribuție prezintă o formă clasică în formă de clopot, consolidând o parte semnificativă a masei sale, impresionant de aproape de medie.
Pe de altă parte, aparițiile valorilor spre final sunt destul de rare. Folosirea unui astfel de a priori afirmă în mod efectiv convingerea că majoritatea ponderilor modelului trebuie să se încadreze într-un interval restrâns definit , foarte aproape de valoarea medie cu doar câteva valori excepționale. Aceasta este o credință rezonabilă de urmat, luând în considerare fenomenele din lumea reală și circumstanțele non-ideale.
Efectele unui model bayesian, însă, sunt și mai interesante când observați că utilizarea acestor distribuții anterioare (și procesul MAP ) generează rezultate uimitor de similare, dacă nu egale cu cele rezolvate prin efectuarea MLE în sensul clasic, ajutat cu unele regularizări suplimentare.
Este foarte amuzant de observat că doar prin constrângerea greutăților modelului „acceptate” cu precedentul, ajungem să creăm un regulator.
În general, Bayesian Machine Learning evoluează rapid ca un subdomeniu al învățării automate, iar dezvoltarea ulterioară și incursiunile în canonul stabilit par a fi un rezultat destul de natural și probabil al ritmului actual de progrese în hardware-ul computațional și statistic.
Citiți: Rețele Bayesiene
Diferitele metode ale învățării automate bayesiene
Există trei abordări în mare măsură acceptate ale învățării automate bayesiane, și anume MAP , MCMC și procesul „Gauss”.
Învățare automată bayesiană cu MAP: Maximum A Posterior
MAP se bucură de distincția de a fi primul pas către adevărata învățare automată bayesiană. Cu toate acestea, este limitată în capacitatea sa de a calcula ceva la fel de rudimentar ca o estimare punctuală, așa cum se referă în mod obișnuit de către statisticienii cu experiență.
Problema cu estimările punctuale este că acestea nu dezvăluie prea multe despre un parametru, altul decât setarea optimă. Analiștii și statisticienii caută adesea informații suplimentare, valoroase, de exemplu, probabilitatea ca valoarea unui anumit parametru să se încadreze în acest interval predefinit. La urma urmei, acolo se află adevărata putere de predicție a învățării automate bayesiane.
Învățare automată bayesiană cu MCMC: Lanțul Markov Monte Carlo
Markov Chain Monte Carlo, cunoscut și sub numele de MCMC, este un algoritm popular și celebrat „umbrelă”, aplicat printr-un set de metode subsidiare celebre, cum ar fi Gibbs și Slice Sampling.
Și în timp ce matematica MCMC este în general considerată dificilă, rămâne la fel de intrigantă și impresionantă. Punctul culminant al acestor metode subsidiare este construirea unui lanț Markov cunoscut, stabilindu-se în continuare într-o distribuție care este echivalentă cu cea posterioară.
Mulți algoritmi succesivi au optat pentru a îmbunătăți metoda MCMC prin includerea informațiilor de gradient în încercarea de a permite analiștilor să navigheze în spațiul parametrilor cu o eficiență sporită.
Cu toate acestea, există modalități mai simple de a obține această precizie. De exemplu, există echivalente de regresie liniară și logistică bayesiene, în care analiștii folosesc Aproximația Laplace . O aproximare analitică (care poate fi explicată pe hârtie) a distribuției posterioare este ceea ce deosebește acest proces.
Trebuie citit: Bayes naiv explicat
Învățare automată bayesiană cu procesul gaussian
Procesul gaussian este un proces stocastic, cu condiții gaussiene stricte fiind impuse tuturor variabilelor constitutive, aleatorii. Acestea funcționează prin determinarea unei distribuții de probabilitate în spațiul tuturor liniilor posibile și apoi selectând linia care este cel mai probabil să fie predictorul real, luând în considerare datele.
Aceste procese ajung să permită analiștilor să efectueze regresii în spațiul funcțional. Având în vedere că întreaga distribuție posterioară este calculată analitic în această metodă, aceasta este, fără îndoială, estimarea bayesiană la cea mai adevărată, și, prin urmare, atât din punct de vedere statistic, cât și logic, cea mai admirabilă.
Dacă doriți să aflați mai multe despre carierele în învățarea automată și inteligența artificială, consultați IIT Madras și Certificarea avansată upGrad în învățare automată și cloud.