Apprentissage automatique bayésien - Explorer un changement de paradigme dans la modélisation des données statistiques
Publié: 2020-11-24Table des matières
Qu'est-ce que l'apprentissage automatique bayésien ?
L'apprentissage automatique bayésien (également connu sous le nom de Bayesian ML) est une approche systématique pour construire des modèles statistiques, basée sur le théorème de Bayes.
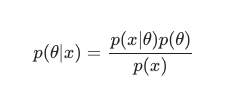Tout problème d'apprentissage automatique standard comprend deux ensembles de données principaux qui doivent être analysés :
- Un ensemble complet de données d'entraînement
- Une collection de toutes les entrées disponibles et de toutes les sorties enregistrées
L'approche traditionnelle d'analyse de ces données pour la modélisation consiste à déterminer certains modèles qui peuvent être cartographiés entre ces ensembles de données. Un analyste assemblera généralement un modèle pour déterminer la correspondance entre ceux-ci, et l'approche résultante est une méthode très déterministe pour générer des prédictions pour une variable cible.
Le seul problème est qu'il n'y a absolument aucun moyen d'expliquer ce qui se passe à l' intérieur de ce modèle avec un ensemble clair de définitions. Tout ce qui est accompli, essentiellement, est la minimisation de certaines fonctions de perte sur l'ensemble de données d'apprentissage - mais cela ne se qualifie guère comme une véritable modélisation.
Un modèle idéal (et de préférence sans perte) implique un résumé objectif des paramètres inhérents au modèle, complété par des œufs de Pâques statistiques (tels que des intervalles de confiance) qui peuvent être définis et défendus dans le langage des probabilités mathématiques. Ce scénario "idéal" est ce que l'apprentissage automatique bayésien se propose d'accomplir.
Les objectifs (et la magie) de l'apprentissage automatique bayésien
L'objectif principal de l'apprentissage automatique bayésien est d'estimer la distribution a posteriori , compte tenu de la vraisemblance (une estimation dérivée des données d'apprentissage) et de la distribution a priori .
Lors de la formation d'un modèle d'apprentissage automatique régulier, c'est exactement ce que nous finissons par faire en théorie et en pratique. Les analystes sont connus pour effectuer des itérations successives de l' estimation du maximum de vraisemblance sur les données d'apprentissage, mettant ainsi à jour les paramètres du modèle d'une manière qui maximise la probabilité de voir les Cela conduit à un problème de poule et d'œuf, que l'apprentissage automatique bayésien vise à résoudre magnifiquement.
Les choses prennent une tournure entièrement différente dans un cas donné où un analyste cherche à maximiser la distribution postérieure , en supposant que les données d'apprentissage sont fixes, et en déterminant ainsi la probabilité de tout réglage de paramètre qui accompagne lesdites données. Ce processus est appelé Maximum A Posteriori , abrégé en MAP . Une façon plus facile de saisir ce concept est de le penser en termes de fonction de vraisemblance .
En tenant compte du théorème de Bayes , le postérieur peut être défini comme :
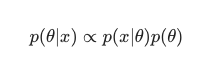
Dans ce scénario, nous omettons le dénominateur en tant que simple mesure anti-redondance. Tout ce qui ne cause pas de dépendance au modèle peut être ignoré dans la procédure de maximisation. Cette pièce clé du puzzle, la distribution a priori, est ce qui permet aux modèles bayésiens de se démarquer par rapport à leurs homologues classiques entraînés par MLE.
Les analystes peuvent souvent faire des hypothèses raisonnables sur la pertinence d'une configuration de paramètre spécifique, ce qui contribue grandement à coder leurs croyances sur ces paramètres avant même de les avoir vus en temps réel. Il est relativement courant, par exemple, d'utiliser un a priori gaussien sur les paramètres du modèle.
L'analyste suppose ici que ces paramètres ont été tirés d'une distribution normale, avec un certain affichage de la moyenne et de la variance. Ce type de distribution présente une forme classique en cloche, consolidant une partie importante de sa masse, impressionnante proche de la moyenne.
D'autre part, les occurrences de valeurs vers la fin sont assez rares. L'utilisation d'un tel a priori énonce effectivement la conviction que la majorité des poids du modèle doivent s'inscrire dans une plage étroite définie , très proche de la valeur moyenne avec seulement quelques valeurs aberrantes exceptionnelles. Il s'agit d'une croyance raisonnable à poursuivre, en tenant compte des phénomènes du monde réel et des circonstances non idéales.
Les effets d'un modèle bayésien sont cependant encore plus intéressants lorsque l'on observe que l'utilisation de ces distributions a priori (et du processus MAP ) génère des résultats étonnamment similaires, voire égaux à ceux résolus en effectuant la MLE au sens classique, aidé par une régularisation supplémentaire.
Il est très amusant de constater qu'à force de contraindre les poids du modèle « accepté » avec le prior, on finit par créer un régularisateur.
Dans l'ensemble, l'apprentissage automatique bayésien évolue rapidement en tant que sous-domaine de l'apprentissage automatique, et le développement et les incursions dans le canon établi semblent être un résultat plutôt naturel et probable du rythme actuel des progrès du matériel informatique et statistique.
Lire : Réseaux bayésiens
Les différentes méthodes d'apprentissage automatique bayésien
Il existe trois approches largement acceptées de l'apprentissage automatique bayésien, à savoir MAP , MCMC et le processus « gaussien ».
Apprentissage automatique bayésien avec MAP : maximum a posteriori
MAP a la particularité d'être la première étape vers un véritable apprentissage automatique bayésien. Cependant, il est limité dans sa capacité à calculer quelque chose d'aussi rudimentaire qu'une estimation ponctuelle, comme l'appellent couramment les statisticiens expérimentés.
Le problème avec les estimations ponctuelles est qu'elles ne révèlent pas grand-chose sur un paramètre autre que son réglage optimal. Les analystes et les statisticiens sont souvent à la recherche d'informations essentielles supplémentaires, par exemple, la probabilité que la valeur d'un certain paramètre se situe dans cette plage prédéfinie. Après tout, c'est là que réside le véritable pouvoir prédictif du Bayesian Machine Learning.
Apprentissage automatique bayésien avec MCMC : Chaîne de Markov Monte Carlo
Markov Chain Monte Carlo, également connu sous le nom de MCMC, est un algorithme «parapluie» populaire et célèbre, appliqué via un ensemble de méthodes subsidiaires célèbres telles que Gibbs et Slice Sampling.
Et bien que les mathématiques de MCMC soient généralement considérées comme difficiles, elles restent tout aussi intrigantes et impressionnantes. Le point culminant de ces méthodes subsidiaires est la construction d'une chaîne de Markov connue, s'installant ensuite dans une distribution équivalente à la postérieure.
De nombreux algorithmes successifs ont choisi d'améliorer la méthode MCMC en incluant des informations de gradient dans le but de permettre aux analystes de naviguer dans l'espace des paramètres avec une efficacité accrue.
Il existe cependant des moyens plus simples d'atteindre cette précision. Par exemple, il existe des équivalents bayésiens de régression linéaire et logistique, dans lesquels les analystes utilisent l' approximation de Laplace . Une approximation analytique (qui peut être expliquée sur papier) de la distribution a posteriori est ce qui distingue ce processus.
Doit lire: Naive Bayes expliqué
Apprentissage automatique bayésien avec le processus gaussien
Le processus gaussien est un processus stochastique, avec des conditions gaussiennes strictes imposées à toutes les variables aléatoires constitutives. Ils fonctionnent en déterminant une distribution de probabilité sur l'espace de toutes les lignes possibles, puis en sélectionnant la ligne la plus susceptible d'être le prédicteur réel, en tenant compte des données.
Ces processus finissent par permettre aux analystes d'effectuer une régression dans l'espace des fonctions. Étant donné que toute la distribution postérieure est calculée analytiquement dans cette méthode, il s'agit sans aucun doute de l'estimation bayésienne la plus vraie, et donc à la fois statistiquement et logiquement, la plus admirable.
Si vous souhaitez en savoir plus sur les carrières dans l'apprentissage automatique et l'intelligence artificielle, consultez IIT Madras et la certification avancée d'upGrad en apprentissage automatique et cloud.