K تعني Clustering Matlab [مع كود المصدر]

يعد تجميع الوسائل K أحد الأساليب الأكثر استخدامًا من قِبل متخصصي البيانات. نظرًا لفعالية الخوارزمية ، فهي مطلوبة من قبل العديد من الصناعات في مختلف التطبيقات.

تتطلب وظيفة عالم البيانات تنفيذ التجميع في العديد من المراحل. تعتمد العديد من المشاريع واسعة النطاق حاليًا على خوارزمية التجميع وقد رفعت بشكل كبير من مستوى طلب متخصصي علوم البيانات.

واحدة من تلك الخوارزميات هي K-mean clustering ، وهي الفكرة الأساسية لهذه المقالة وتنفيذها مع شفرة مصدر MATLAB.

قبل تعليق الموضوع ، دعنا نلقي نظرة سريعة على ماهية Clustering وأهميتها وكيف يمكن تنفيذها في الحياة الواقعية. بنهاية المنشور ، ستعرف مدى أهمية هذه الخوارزمية لفهم البيانات في مجموعات كبيرة.

ما هو التجميع؟

البيانات هي المكون الأكثر أهمية لأي تطبيق ، والعنقدة ليست سوى تراكم لنقاط بيانات متشابهة مجتمعة. كما يحدد الاسم بوضوح ، فإن التجميع هو عملية تقسيم جزء كبير من البيانات إلى مجموعات فرعية أو مجموعات فقط بناءً على نمط البيانات.

في التعلم الآلي ، يتم تطبيق التجميع في حالة عدم توفر بيانات محددة مسبقًا. الهدف النهائي هو تجميع البيانات في فئات ذات تشابه عالي داخل الطبقة.

يستخدم التجميع لاستكشاف البيانات. بعض الأمثلة الواقعية حيث يمكن استخدامها هي في تجزئة السوق للعثور على عملاء لديهم سلوكيات مماثلة ، وتجزئة / ضغط الصور ، وتجميع المستندات مع مواضيع متعددة ، وما إلى ذلك.

إنها خطوة ضرورية قبل معالجة البيانات لتحديد المجموعات المتجانسة لبناء النماذج الخاضعة للإشراف. تعد مجموعة K-Means عبارة عن خوارزمية تعلم غير خاضعة للإشراف حيث يتعين علينا البحث عن البيانات لدمج الملاحظات المتشابهة وتشكيل مجموعات متميزة.

دعنا نلقي نظرة على خوارزمية K-Means ، والتي تعد واحدة من أكثر خوارزميات المجموعات تطبيقاً وأبسطها.

K-Means Clustering

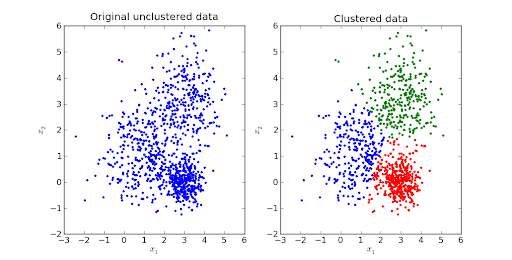
مصدر الصورة

تعد K-mean clustering واحدة من أكثر خوارزميات التعلم الآلي غير الخاضعة للرقابة المرغوبة.

توصل الخوارزميات غير الخاضعة للإشراف إلى استنتاجات من مجموعات البيانات باستخدام متجهات الإدخال دون الرجوع إلى النتائج المصنفة.

إنها خوارزمية تكرارية قائمة على المسافة أو تستند إلى النقطه الوسطى تفصل مجموعة البيانات إلى مجموعات فرعية مميزة K (مجموعات) حيث تنتمي كل نقطة بيانات إلى مجموعة واحدة . يتم زيادة تشابه نقاط البيانات داخل المجموعة ، ويتم الاحتفاظ بالمسافة بين المجموعات في أفضل حالاتها.

يتم الاحتفاظ بالمسافة بين نقاط البيانات والنقطة الوسطى للمجموعة عند الحد الأدنى ، مثل المسافة الإقليدية. في K-Means ، ترتبط كل مجموعة بنقطة مركزية. الهدف الأساسي هو تقليل المسافات بين النقاط والنقطة الوسطى العنقودية ذات الصلة.

كيف يعمل K-Means Clustering؟

نظرًا لأن عملية التجميع تعني إجراء العديد من التكرارات ، فإن خوارزمية K-Means لها طريقة فريدة للعمل. فيما يلي شرح تفصيلي للطريقة التي يعمل بها:

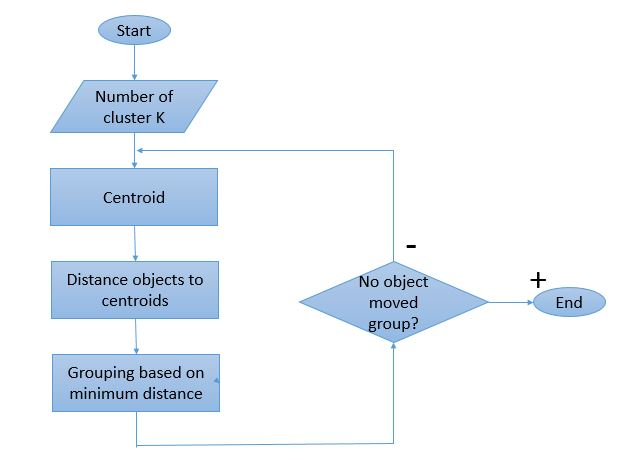
مصدر الصورة

الخطوة 1: في البداية ، حدد عدد المجموعات " الخطوة 2: تهيئة نقاط بيانات K العشوائية كنقاط مركزية لكل مجموعة.

إذا كانت هناك مجموعتان ، فإن قيمة "K" ستكون 2.

الخطوة 3: قم بإجراء العديد من التكرارات حتى لا تتغير نقاط البيانات المخصصة للمجموعات.

الخطوة 4: احسب مجموع المسافة المربعة بين نقاط البيانات والنقط الوسطى.

الخطوة 5: قم بتخصيص كل نقطة بيانات لأقرب مجموعة (centroid) لتقليل المسافة.

الخطوة 6: خذ متوسط ​​النقط الوسطى من المجموعات التي تنتمي إلى بعضها البعض.

هذه عملية تكرار واحدة يتم إجراؤها لحساب النقطه الوسطى وتعيين النقاط إلى العنقود بناءً على بعدهم عن النقطه الوسطى. بمجرد تحديد جميع النقط الوسطى ، تتوقف العملية.

مثال توضيحي يصور تنفيذ K-Means Clustering

بيان: تريد ماكدونالدز ، إحدى سلاسل المطاعم الشهيرة ، فتح سلسلة من المنافذ في جميع أنحاء كاليفورنيا وتريد معرفة المواقع التي ستجلب لهم أقصى عائد.

ماذا لدى ماكدونالدز بالفعل؟

Ø حضور قوي في التجارة الإلكترونية

Ø بيانات العملاء عبر الإنترنت لتحليل المواقع من حيث يتم تقديم الطلبات بشكل متكرر

التحديات المحتملة التي يمكن أن يواجهوها

• تحليل المناطق التي تصدر منها الأوامر بشكل متكرر.
• افهم عدد المنافذ التي سيتم فتحها في المنطقة
• حدد مواقع المنافذ داخل جميع المناطق للحفاظ على أدنى مسافة بين المتجر ونقاط التسليم.

كل هذه النقاط تحتاج إلى الكثير من التحليل والرياضيات للعمل عليها.

كيف يمكن استخدام طريقة التجميع K-mean هنا؟

باستخدام قيمة محددة مسبقًا لـ K ، يمكن تنفيذ خوارزمية K-mean في الخطوات التالية:

• تحديد مواقع المخزن باستخدام قسم K للكائنات في مجموعات فرعية غير فارغة K.
• تحديد النقطه الوسطى العنقودية للقسم.
• تخصيص كل موقع لمجموعة معينة.
• حساب المسافات من كل موقع وتخصيص نقاط للعنقود حيث تكون المسافة الدنيا مع المخرج.
• بعد تكرار واحد ، إعادة تخصيص النقاط ، ابحث عن النقطه الوسطى للعنقود الجديد.

وبالمثل ، يمكن تطبيق خوارزمية K-Means Clustering على مجموعة متنوعة من التطبيقات في نطاقات متنوعة. صناعة الضيافة ، وأقسام التحقيق في الجرائم ، وتغيير حجم الصورة ، على سبيل المثال لا الحصر.

يتم تنفيذ خوارزمية K-Means باستخدام العديد من اللغات مثل R و Python و MATLAB وما إلى ذلك. في القسم التالي ، سننظر في كيفية تطبيق K-Means Clustering MATLAB.

قراءة: أنواع الوظائف في Matlab

K- يعني خوارزمية باستخدام MATLAB

K-Means هي خوارزمية مستخدمة إلى حد كبير يستخدمها العديد من المتخصصين الذين يتعاملون مع علوم البيانات والتعلم الآلي والذكاء الاصطناعي والتشفير والأمن السيبراني.

الهدف الأساسي من استخدام هذه الخوارزمية هو معرفة النقطه الوسطى لكل عنقود. البيانات المعطاة للمبرمج غير متجانسة. هنا هو رمز MATLAB لرسم النقطه الوسطى من كل عنقود وتعيين إحداثيات كل النقطه الوسطى:

العنقودية MATLAB

رمز:

rng الافتراضي ؛ ٪ للتكاثر

X = [randn (100،2) * 0.75 + واحد (100،2) ؛

randn (100،2) * 0.5-one (100،2)] ؛

يختار = statset ('Display'، 'final') ؛

[idx، C] = kmeans (X، 4، 'Distance'، 'cityblock'، 'Replicates'، 5، 'Options'، اختيارات)؛

المؤامرة (X (idx == 1،1) ، X (idx == 1،2) ، 'r.' ، 'MarkerSize' ، 12) ؛

يتمسك؛

المؤامرة (X (idx == 2،1) ، X (idx == 2،2) ، 'b.' ، 'MarkerSize' ، 12) ؛

المؤامرة (X (idx == 3،1) ، X (idx == 3،2) ، 'g.' ، 'MarkerSize' ، 12) ؛

المؤامرة (X (idx == 4،1) ، X (idx == 4،2) ، 'y.' ، 'MarkerSize' ، 12) ؛

قطعة الأرض (C (:، 1)، C (:، 2)، 'Kx'، 'MarkerSize'، 15، 'LineWidth'، 3) ؛

أسطورة ('Cluster 1 ′،' Cluster 2 ′، 'Cluster 3 ′،' Cluster 4 ′، 'Centroids'، 'Location'، 'NW')؛

العنوان ("تعيينات الكتلة والنقاط الوسطى") ؛

خارج القبضة؛

بالنسبة إلى i = 1: الحجم (C ، 1)

display (['Centroid'، num2str (i)، ': X1 ='، num2str (C (i، 1))، '؛ X2 ='، num2str (C (i، 2))]) ؛

نهاية

انتاج:

تظهر نافذة MATLAB أربع مجموعات و Centroids كل منها

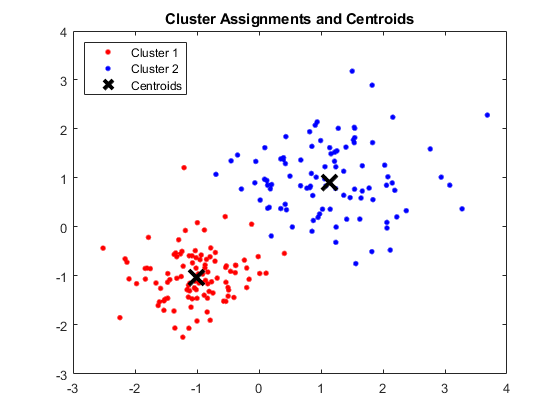
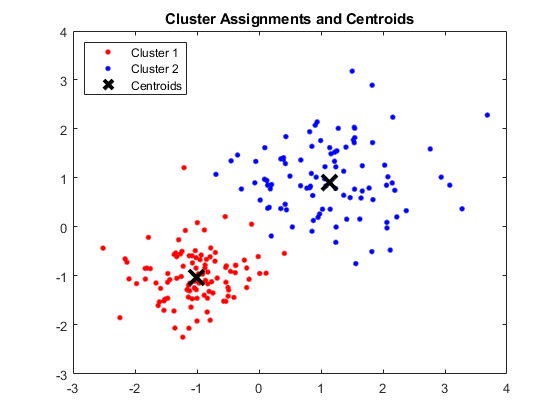
مصدر الصورة

نتائج:

النقط الوسطى التي تم الحصول عليها هي كما يلي:

1. قيمة X1 & X2 لـ Centroid 1: 1.3661 ؛ 1.7232
2. قيمة X1 & X2 لـ Centroid 2: -1.015 ؛ -1.053
3. قيمة X1 & X2 لـ Centroid 3: 1.6565 ؛ 0.36376
4. قيمة X1 & X2 لـ Centroid 4: 0.35134 ؛ 0.85358

بعض مجالات العمل حيث يمكن تنفيذ مجموعات K-Means

K-mean clustering عبارة عن خوارزمية متعددة الاستخدامات ويمكن استخدامها للعديد من حالات استخدام الأعمال لأي نوع من التجميع. بعض الأمثلة هي:

Ø الفصل السلوكي:

• التقسيم باستخدام سجل الشراء
• التقسيم باستخدام أنشطة التطبيق أو الموقع أو النظام الأساسي
• تحديد صورة العملاء بناءً على اهتماماتهم
• إنشاء الملف الشخصي مع أنشطة المراقبة

Ø تحجيم الصورة

• ضغط الصور باستخدام بايثون

Ø قياسات المستشعر:

• كشف أنواع نشاط مجسات الحركة
• صور المجموعة
• تقسيم الصوت
• مجموعات مراقبة الصحة الموضعية

Ø تحديد الروبوتات أو الحالات الشاذة:

• افصل مجموعات الأنشطة عن الروبوتات
• قم بعمل مجموعة من الأنشطة الصالحة لتنظيف الكشف الخارجى

Ø تصنيف المخزون:

• عمل مجموعات المخزون حسب نشاط المبيعات
• قم بعمل مجموعات المخزون عن طريق مقاييس التصنيع

مزايا K-Means Clustering

هناك سبب يجعل كبار المحترفين يفضلون خوارزمية التجميع K-Means. بعض الفوائد التي يقدمها:

• إنها خوارزمية سريعة وقوية وسهلة الفهم.
• الكفاءة النهائية عالية نسبيًا
• يقدم نتائج استثنائية عندما تختلف مجموعات البيانات عن بعضها البعض. بالنسبة لقيم المتغيرات الأعلى ، تعمل K-Means بشكل أسرع نسبيًا
• تعتبر المجموعات التي يتم إنتاجها باستخدام K-Means أكثر إحكامًا نسبيًا من طرق التجميع الأخرى.

يجب أن تقرأ: أنواع بيانات MATLAB

خاتمة

K- يعني التجميع هو نهج واسع الاستخدام لتحليل مجموعات البيانات. بمجرد حصولك على القيادة ، يكون من الأسهل فهم وتطبيق وتقديم النتائج بسرعة.

نأمل مع هذا المقال ؛ يمكننا أن نقدم لك تقنية التحليل هذه. لأية استفسارات بخصوص خوارزمية K-mean ، لا تتردد في التعليق أدناه.

علاوة على ذلك ، إذا كان مجال الدراسة هذا يثير اهتمامك ، فقم بإلقاء نظرة على دبلوم PG في التعلم الآلي وبرنامج الذكاء الاصطناعي الذي تم تصميمه خصيصًا للمهنيين العاملين الذين يقدمون أكثر من 30 دراسة حالة ومهمة ، و 25+ جلسة إرشادية من خبراء الصناعة ، و 10 أيدي عملية- في مشاريع Capstone ، 450+ ساعة من التعلم والمساعدة في التوظيف.

ما هو K Means clustering في التعلم الآلي؟

هذه خوارزمية تجميع شائعة تُستخدم في التعلم الآلي غير الخاضع للإشراف. تعمل خوارزمية يعني K على مبدأ تحديد النقط الوسطى K بشكل عشوائي. من الخطوة التالية ، تحاول الخوارزمية تعظيم الإجمالي الكلي ضمن مسافة الكتلة وتقليل المسافة الكلية بين الكتلة. خوارزمية يعني K هي نهج تكراري. في كل تكرار ، فإنه يحدد K يعني من مجموعة النقط الوسطى الحالية. ثم تقوم الخوارزمية بتعيين كل ملاحظة لأقرب متوسط ​​K. يتم حساب المسافة بين مجموعتين بناءً على المسافة بين أقرب ملاحظتين. يتم تعريف Centroid للكتلة على أنها متوسط ​​جميع الملاحظات في الكتلة.

ما هي حدود خوارزمية المجموعات K Means؟

هناك بعض القيود على وسائل K والتي يجب أن تضعها في اعتبارك عند استخدامها. يعني K ليست قوية للقيم المتطرفة. لا تعمل خوارزمية الوسائل K بشكل جيد إلا عندما تكون جميع نقاط البيانات الخاصة بك على نفس المسافة تقريبًا من النقطه الوسطى. إذا كانت بعض نقاط البيانات الخاصة بك بعيدة عن النقطه الوسطى ، فسيؤدي ذلك إلى تحيز تعيين نقاط البيانات الأخرى إلى المجموعات. لا تضمن وسائل K حلاً فريدًا. إذا كان لديك أكثر من مجموعة واحدة من النقاط ، فليس هناك ما يضمن أن K Means ستعيد نفس العدد من المجموعات في كل مرة يتم فيها تشغيل الخوارزمية. يعني K يتقارب ببطء. تتقارب الخوارزمية ببطء شديد ، حتى في مجموعات البيانات الصغيرة.

ما هي مزايا K Means clustering؟

إنه فعال لكل من الأبعاد الفردية والمتعددة. إنه قابل للتطبيق في كلا البعدين وثلاثة أبعاد. إنه مفيد بشكل خاص في المواقف التي يوجد فيها العديد من المجموعات. يتم الحصول على المجموعات في منتصف نقطة البيانات. يتم حساب متوسط ​​القيمة لكل مجموعة. يتم تقسيم كل نقطة على الانحراف المعياري ثم يتم مقارنتها بالقيمة المتوسطة. يتم حساب متوسط ​​القيمة والانحراف المعياري لجميع المجموعات والنقاط.