K signifie clustering Matlab [avec code source]

Le clustering K-means est l'une des techniques les plus couramment utilisées par les professionnels des données. En raison de l'efficacité de l'algorithme, il est demandé par de nombreuses industries dans diverses applications.

Le travail d'un data scientist nécessite la mise en œuvre du clustering en plusieurs étapes. De nombreux projets à grande échelle sont actuellement basés sur l'algorithme de clustering et ont considérablement relevé la barre de la demande des professionnels de la science des données.

L'un de ces algorithmes est le clustering K-means, qui est l'idée de base de cet article et son implémentation avec le code source MATLAB.

Avant de saisir le sujet, examinons rapidement ce qu'est le clustering, sa signification et comment il peut être mis en œuvre dans la vie réelle. À la fin de l'article, vous saurez à quel point cet algorithme est crucial pour comprendre les données dans de grands ensembles.

Qu'est-ce que le clustering ?

Les données sont le composant le plus critique pour toute application, et un cluster n'est rien d'autre qu'une accumulation de points de données similaires combinés. Comme son nom le définit clairement, le clustering est le processus de division d'une grande quantité de données en sous-groupes ou uniquement en clusters en fonction du modèle de données.

Dans l'apprentissage automatique, le clustering est appliqué lorsqu'il n'y a pas de données prédéfinies disponibles. Le but ultime est de regrouper les données en classes avec une forte similarité intra-classe.

Le clustering est utilisé pour explorer les données. Certains exemples concrets où il peut être utilisé sont la segmentation du marché pour trouver des clients ayant des comportements similaires, la segmentation/compression d'images, le regroupement de documents avec plusieurs sujets, etc.

C'est une étape nécessaire avant le traitement des données pour identifier des groupes homogènes pour construire des modèles supervisés. Le clustering K-Means est un algorithme d'apprentissage non supervisé car nous devons rechercher des données pour intégrer des observations similaires et former des groupes distincts.

Jetons un coup d'œil à l' algorithme K-Means , qui est l'un des algorithmes de clustering les plus appliqués et les plus simples.

Clustering K-Means

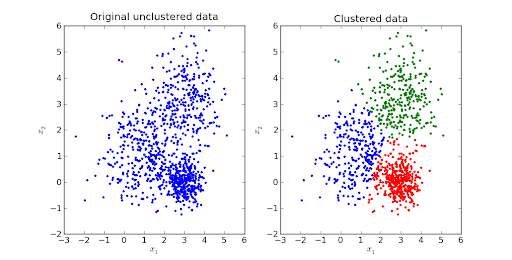
Source des images

Le clustering K-means est l'un des algorithmes d'apprentissage automatique non supervisé les plus recherchés.

Les algorithmes non supervisés tirent des conclusions à partir d'ensembles de données à l'aide de vecteurs d'entrée sans se référer aux résultats étiquetés.

Il s'agit d'un algorithme itératif basé sur la distance ou sur le centroïde qui sépare l'ensemble de données en K sous-groupes distincts (clusters) où chaque point de données appartient à un groupe . La similarité des points de données intra-cluster est augmentée et la distance entre les clusters est maintenue optimale.

La distance entre les points de données et le centroïde du cluster est maintenue à un minimum, comme la distance euclidienne. Dans K-Means, chaque cluster est lié à un centroïde. L'objectif principal est de minimiser les distances entre les points et le centre de gravité du cluster respectif.

Comment fonctionne le clustering K-Means ?

Comme le processus de clustering implique plusieurs itérations à effectuer, l'algorithme K-Means a un mode de fonctionnement unique. Voici une explication étape par étape de son fonctionnement :

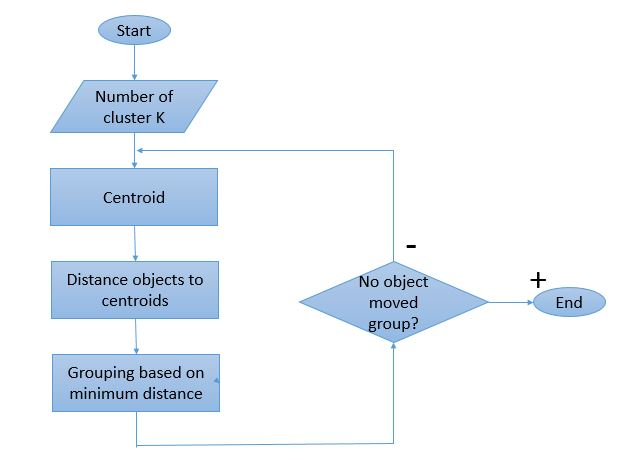
Source des images

Étape 1 : Dans un premier temps, définissez le nombre de clusters ' Étape 2 : Initialisez des points de données K aléatoires en tant que centroïdes pour chaque cluster.

S'il y a 2 clusters, la valeur de 'K' sera 2.

Étape 3 : Effectuez plusieurs itérations jusqu'à ce que les points de données attribués aux clusters ne changent pas.

Étape 4 : Calculez la somme de la distance au carré entre les points de données et les centroïdes.

Étape 5 : Attribuez chaque point de données au cluster le plus proche (centroïde) pour minimiser la distance.

Étape 6 : Faites une moyenne des centroïdes des clusters appartenant les uns aux autres.

Il s'agit d'un processus d'itération unique effectué pour calculer le centroïde et attribuer les points au cluster en fonction de leur distance par rapport au centroïde. Une fois tous les centroïdes définis, le processus est arrêté.

Un exemple illustratif illustrant la mise en œuvre du clustering K-Means

Déclaration : L'une des célèbres chaînes alimentaires, McDonald's souhaite ouvrir une chaîne de points de vente à travers la Californie et souhaite découvrir les emplacements qui leur rapporteront le maximum de revenus.

Qu'est-ce que McDonald's a déjà ?

Ø Une forte présence e-commerce

Ø Données clients en ligne pour analyser les emplacements d'où les commandes sont fréquemment passées

Défis éventuels auxquels ils pourraient être confrontés

• Analyser les zones d'où les commandes sont fréquemment passées.
• Comprendre le nombre de points de vente à ouvrir dans la zone
• Déterminez les emplacements des points de vente dans toutes les zones afin de maintenir une distance minimale entre le magasin et les points de livraison.

Tous ces points nécessitent beaucoup d'analyse et de mathématiques pour travailler.

Comment la méthode de clustering K-means peut-elle être utilisée ici ?

Avec une valeur prédéfinie de K, l'algorithme K-means peut être implémenté dans les étapes suivantes :

• Identification des emplacements de stockage avec K Partition des objets en K sous-ensembles non vides.
• Détermination des centroïdes de cluster de la partition.
• Affectation de chaque emplacement à un cluster spécifique.
• Calculer les distances de chaque emplacement et allouer des points au cluster où la distance est minimale avec la prise.
• Après une itération, en réattribuant les points, trouvez le centroïde du nouveau cluster formé.

De même, l'algorithme K-Means Clustering peut être appliqué à une variété d'applications à des échelles variées. L'industrie hôtelière, les services d'enquête criminelle et le redimensionnement d'images, pour n'en nommer que quelques-uns.

L'algorithme K-Means est implémenté à l'aide de nombreux langages tels que R , Python, MATLAB, etc. Dans la section suivante, nous verrons comment K-Means Clustering MATLAB est appliqué.

Lire : Types de fonctions dans Matlab

Algorithme K-Means utilisant MATLAB

K-Means est un algorithme largement utilisé par de nombreux professionnels traitant de la science des données, de l'apprentissage automatique, de l'intelligence artificielle, de la cryptographie et de la cybersécurité.

L'objectif principal de l'utilisation de cet algorithme est de trouver le centroïde de chaque cluster. Les données fournies à un programmeur sont hétérogènes. Voici le code MATLAB pour tracer le centroïde de chaque cluster et attribuer les coordonnées de chaque centroïde :

Clustering MATLAB

Code:

rng par défaut ; % Pour la reproductibilité

X = [randn(100,2)*0.75+uns(100,2);

randn(100,2)*0,5-uns(100,2)] ;

opts=statset('Affichage','final');

[idx,C]=kmeans(X,4,'Distance','cityblock','Replicates',5,'Options',opts);

plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12);

attendez;

plot(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12);

plot(X(idx==3,1),X(idx==3,2),'g.','MarkerSize',12);

plot(X(idx==4,1),X(idx==4,2),'y.','MarkerSize',12);

plot(C(:,1),C(:,2),'Kx','MarkerSize',15,'LineWidth',3);

legend('Cluster 1','Cluster 2','Cluster 3','Cluster 4','Centroids', 'Location','NW');

title('Affectations de cluster et centroïdes');

attendre;

pour i=1:taille(C, 1)

display(['Centroid ', num2str(i), ': X1 = ', num2str(C(i, 1)), '; X2 = ', num2str(C(i, 2))]);

finir

Sortir:

Fenêtre MATLAB montrant quatre clusters et leurs centroïdes respectifs

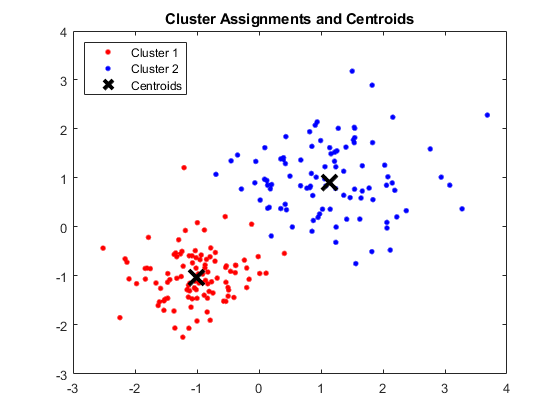
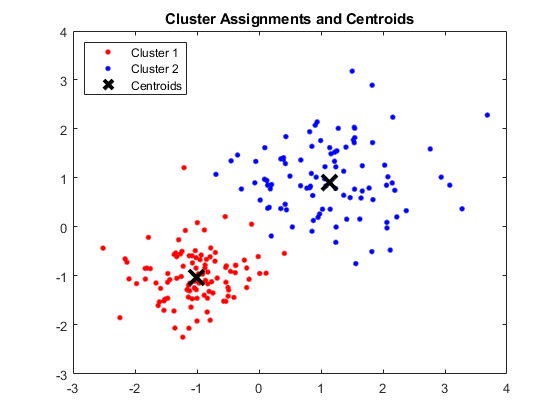
Source des images

Résultats:

Les barycentres obtenus sont les suivants :

1. La valeur de X1 & X2 pour Centroid 1 : 1,3661 ; 1,7232
2. La valeur de X1 & X2 pour Centroid 2 : -1.015 ; -1.053
3. La valeur de X1 & X2 pour Centroid 3 : 1,6565 ; 0,36376
4. La valeur de X1 & X2 pour Centroid 4 : 0,35134 ; 0,85358

Certains domaines d'activité où le clustering K-Means peut être mis en œuvre

Le clustering K-means est un algorithme polyvalent et peut être utilisé pour de nombreux cas d'utilisation commerciale pour tout type de regroupement. Quelques exemples sont:

Ø Ségrégation comportementale :

• Division utilisant l'historique des achats
• Division utilisant des activités d'application, de site Web ou de plate-forme
• Identifier l'image des clients en fonction de leurs centres d'intérêt
• Création de profil avec activités de surveillance

Ø Mise à l'échelle de l'image

• Compression d'images avec Python

Ø Mesures du capteur :

• Détecter les types d'activité des capteurs de mouvement
• Images de groupe
• Diviser le son
• Groupes de surveillance de la santé Spot

Ø Déterminer les bots ou anomalies :

• Séparez les groupes d'activités des bots
• Créer un groupe d'activités valides pour nettoyer la détection des valeurs aberrantes

Ø Classement d'inventaire :

• Faire des groupes d'inventaire par activité de vente
• Créer des groupes d'inventaire en fonction des métriques de fabrication

Avantages du clustering K-Means

Il y a une raison pour laquelle les meilleurs professionnels préfèrent l'algorithme de clustering K-Means. Quelques avantages qu'il offre :

• C'est un algorithme rapide, robuste et facile à comprendre.
• Le rendement final est relativement élevé
• Offre des résultats phénoménaux lorsque les ensembles de données sont différents les uns des autres. Pour des valeurs de variables plus élevées, K-Means fonctionne relativement plus rapidement
• Les clusters produits avec K-Means sont relativement plus serrés que les autres méthodes de clustering.

Doit lire : Types de données MATLAB

Conclusion

Le clustering K-means est une approche largement utilisée pour analyser les clusters de données. Une fois que vous maîtrisez, il est plus facile de comprendre, d'appliquer et de fournir des résultats rapidement.

Nous espérons avec cet article; nous pourrions vous initier à cette technique d'analyse. Pour toute question concernant l'algorithme K-means, n'hésitez pas à commenter ci-dessous.

De plus, si ce domaine d'études vous intéresse, jetez un coup d'œil à notre programme de diplôme PG en apprentissage automatique et IA qui est spécialement conçu pour les professionnels en activité offrant plus de 30 études de cas et missions, plus de 25 sessions de mentorat d'experts de l'industrie, 10 mains pratiques- sur Capstone Projects, plus de 450 heures d'apprentissage et d'aide au placement.

Qu'est-ce que le clustering K Means dans l'apprentissage automatique ?

Il s'agit d'un algorithme de clustering populaire utilisé dans l'apprentissage automatique non supervisé. L'algorithme K Means fonctionne sur le principe de l'identification aléatoire de K centroïdes. À partir de l'étape suivante, l'algorithme essaie de maximiser la distance globale à l'intérieur des clusters et également de minimiser la distance globale entre les clusters. L'algorithme K Means est une approche itérative. À chaque itération, il sélectionne les K Means à partir de l'ensemble actuel de centroïdes. L'algorithme affecte ensuite chaque observation à la moyenne K la plus proche. La distance entre deux clusters est calculée en fonction de la distance entre les deux observations les plus proches. Le centroïde d'un cluster est défini comme la moyenne de toutes les observations du cluster.

Quelles sont les limites de l'algorithme de clustering K Means ?

Il y a certaines limitations de K Means que vous voudrez garder à l'esprit lors de son utilisation. K Means n'est pas robuste aux valeurs aberrantes. L'algorithme K Means ne fonctionne bien que lorsque tous vos points de données sont à peu près à la même distance du centroïde. Si certains de vos points de données sont éloignés du centroïde, cela biaisera l'affectation d'autres points de données aux clusters. K Means ne garantit pas une solution unique. Si vous avez plus d'un cluster de points, il n'y a aucune garantie que K Means renverra le même nombre de clusters à chaque exécution de l'algorithme. K Means converge lentement. L'algorithme converge très lentement, même sur de petits ensembles de données.

Quels sont les avantages du clustering K Means ?

Il est efficace pour les dimensions simples et multiples. Il est applicable en deux et en trois dimensions. Il est particulièrement utile dans les situations où il existe de nombreux clusters. Les grappes sont obtenues au milieu des points de données. Une valeur moyenne est calculée pour chaque cluster. Chaque point est divisé par l'écart-type, puis il est comparé à la valeur moyenne. La valeur moyenne et l'écart type sont calculés pour tous les clusters et points.