K oznacza klastrowanie Matlab [z kodem źródłowym]

Grupowanie K-średnich jest jedną z najczęściej używanych technik przez specjalistów ds. danych. Ze względu na skuteczność algorytmu jest poszukiwany przez wiele branż w różnych zastosowaniach.

Praca analityka danych wymaga wdrożenia klastrowania w wielu etapach. Wiele projektów na dużą skalę jest obecnie opartych na algorytmie klastrowania i drastycznie podniosło poprzeczkę w zakresie zapotrzebowania specjalistów w zakresie analizy danych.

Jednym z takich algorytmów jest klastrowanie K-średnich, które jest podstawową ideą tego artykułu i jego implementacja z kodem źródłowym MATLAB.

Zanim przyjrzymy się tematowi, rzućmy okiem na to, czym jest klastrowanie, jego znaczenie i jak można go zaimplementować w prawdziwym życiu. Pod koniec postu dowiesz się, jak ważny jest ten algorytm dla zrozumienia danych w dużych zbiorach.

Co to jest klastrowanie?

Dane są najbardziej krytycznym składnikiem każdej aplikacji, a klaster to nic innego jak nagromadzenie podobnych punktów danych razem wziętych. Jak sama nazwa jasno określa, klastrowanie to proces dzielenia dużej porcji danych na podgrupy lub tylko klastry na podstawie wzorca danych.

W uczeniu maszynowym klastrowanie jest stosowane, gdy nie ma dostępnych wstępnie zdefiniowanych danych. Ostatecznym celem jest pogrupowanie danych w klasy o wysokim podobieństwie wewnątrzklasowym.

Do eksploracji danych służy klastrowanie. Niektóre przykłady z życia, w których można go użyć, to segmentacja rynku w celu znalezienia klientów o podobnych zachowaniach, segmentacja/kompresja obrazów, grupowanie dokumentów z wieloma tematami itp.

Jest to niezbędny krok przed przetwarzaniem danych w celu zidentyfikowania jednorodnych grup do budowy modeli nadzorowanych. Grupowanie K-średnich to nienadzorowany algorytm uczenia się, ponieważ musimy szukać danych, aby zintegrować podobne obserwacje i utworzyć odrębne grupy.

Przyjrzyjmy się algorytmowi K-średnich , który jest jednym z najczęściej stosowanych i najprostszych algorytmów grupowania.

Klastrowanie K-średnich

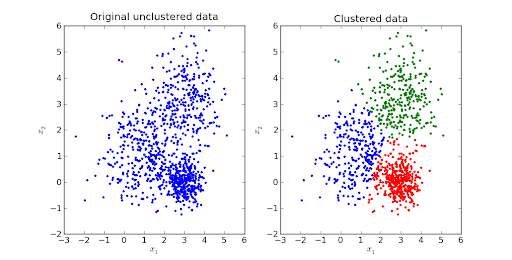
Źródło obrazu

Klastrowanie K-średnich jest jednym z najbardziej pożądanych algorytmów nienadzorowanego uczenia maszynowego.

Nienadzorowane algorytmy wyciągają wnioski ze zbiorów danych przy użyciu wektorów wejściowych bez odwoływania się do oznaczonych wyników.

Jest to iteracyjny algorytm oparty na odległości lub centroidzie, który dzieli zbiór danych na K odrębnych podgrup (klastrów), w których każdy punkt danych należy do jednej grupy . Podobieństwo punktów danych wewnątrz klastra jest zwiększone, a odległość między klastrami jest optymalna.

Odległość między punktami danych a środkiem ciężkości gromady jest utrzymywana na minimalnym poziomie, takim jak odległość euklidesowa. W K-Means każdy klaster jest połączony z centroidem. Głównym celem jest zminimalizowanie odległości między punktami a odpowiednim centroidem klastra.

Jak działa klastrowanie K-Means?

Ponieważ proces grupowania wymaga wykonania kilku iteracji, algorytm K-Means ma unikalny sposób działania. Oto wyjaśnienie krok po kroku, jak to działa:

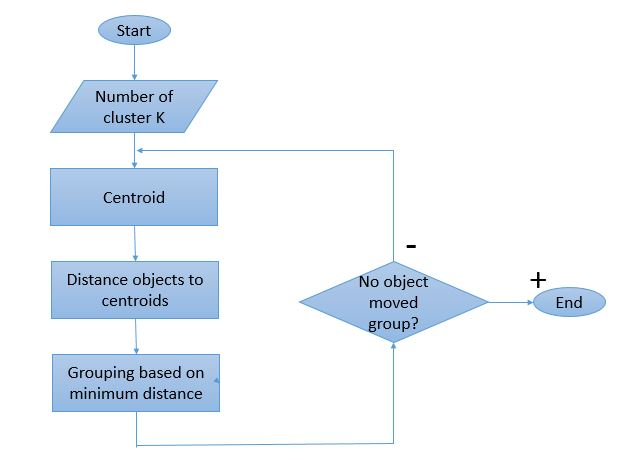
Źródło obrazu

Krok 1: Najpierw zdefiniuj liczbę klastrów „ Krok 2: Zainicjuj losowe punkty danych K jako centroidy dla każdego klastra.

Jeśli istnieją 2 skupienia, wartość „K” wyniesie 2.

Krok 3: Wykonaj kilka iteracji, aż punkty danych przypisane do klastrów nie ulegną zmianie.

Krok 4: Oblicz sumę kwadratu odległości między punktami danych a centroidami.

Krok 5: Przydziel każdy punkt danych do najbliższego klastra (centroidu), aby zminimalizować odległość.

Krok 6: Oblicz średnią z centroidów klastrów należących do siebie.

Jest to pojedynczy proces iteracyjny wykonywany w celu obliczenia centroidu i przypisania punktów do klastra na podstawie ich odległości od centroidu. Po zdefiniowaniu wszystkich centroidów proces zostaje zatrzymany.

Przykład ilustrujący implementację klastrowania K-średnich

Oświadczenie: Jedna ze słynnych sieci spożywczych, McDonald's, chce otworzyć sieć placówek w całej Kalifornii i dowiedzieć się, w jakich lokalizacjach uzyskają maksymalne przychody.

Co już ma McDonald's?

Ø Silna obecność e-commerce

Ø Dane klientów online do analizy lokalizacji, z których często składane są zamówienia

Możliwe wyzwania, z jakimi mogą się zmierzyć

• Analizowanie obszarów, z których często składane są zamówienia.
• Zrozum, ile punktów sprzedaży ma zostać otwartych w okolicy
• Znajdź lokalizacje punktów sprzedaży we wszystkich obszarach, aby zachować minimalną odległość między sklepem a punktami dostawy.

Wszystkie te punkty wymagają dużo analizy i matematyki do pracy.

Jak można tutaj zastosować metodę grupowania K-średnich?

Przy wstępnie zdefiniowanej wartości K algorytm K-średnich można zaimplementować w następujących krokach:

• Identyfikacja lokalizacji sklepów za pomocą K Podział obiektów na K niepuste podzbiory.
• Określanie centroidów klastra partycji.
• Przypisywanie każdej lokalizacji do konkretnego klastra.
• Obliczanie odległości z każdej lokalizacji i przydzielanie punktów do klastra, w którym odległość od wylotu jest minimalna.
• Po jednej iteracji, ponownym przydzieleniu punktów, znajdź środek ciężkości utworzonego nowego klastra.

Podobnie algorytm K-Means Clustering może być stosowany do różnych aplikacji w różnych skalach. Branża hotelarska, wydziały kryminalne i zmiana rozmiaru obrazu, żeby wymienić tylko kilka.

Algorytm K-Means jest zaimplementowany przy użyciu wielu języków, takich jak R , Python, MATLAB, itp. W następnej sekcji przyjrzymy się, jak K-Means Clustering MATLAB jest stosowany.

Przeczytaj: Rodzaje funkcji w Matlab

Algorytm K-średnich przy użyciu MATLAB

K-Means to szeroko stosowany algorytm używany przez wielu profesjonalistów zajmujących się nauką o danych, uczeniem maszynowym, sztuczną inteligencją, kryptografią i cyberbezpieczeństwem.

Podstawowym celem użycia tego algorytmu jest znalezienie środka ciężkości każdego klastra. Dane przekazywane programiście są niejednorodne. Oto kod MATLAB do wykreślenia centroidu każdego klastra i przypisania współrzędnych każdego centroidu:

Klastrowanie MATLAB

Kod:

rng domyślnie; % Dla odtwarzalności

X = [randn(100,2)*0,75+jedynki(100,2);

randn(100,2)*0,5-jedynki(100,2)];

opts=statset('Wyświetlanie','final');

[idx,C]=kmeans(X,4,'Odległość','blok miasta','Repliki',5,'Opcje',opcje);

działka(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12);

trzymać się;

działka(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12);

działka(X(idx==3,1),X(idx==3,2),'g.','MarkerSize',12);

działka(X(idx==4,1),X(idx==4,2),'y.','MarkerSize',12);

działka(C(:,1),C(:,2),'Kx','RozmiarZnacznika',15,'Szerokość Linii',3);

legend('Gromada 1′,'Gromada 2′,'Gromada 3′,'Gromada 4′,'Centroidy', 'Położenie','NW');

title('Przypisania klastra i centroidy');

powstrzymać;

dla i=1:rozmiar(C, 1)

display(['Centroida ', num2str(i), ': X1 = ', num2str(C(i, 1)), '; X2 = ', num2str(C(i, 2))]);

koniec

Wyjście:

Okno MATLAB pokazujące cztery skupienia i odpowiednie centroidy

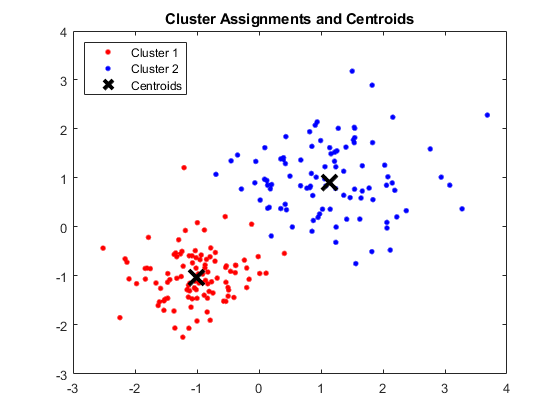
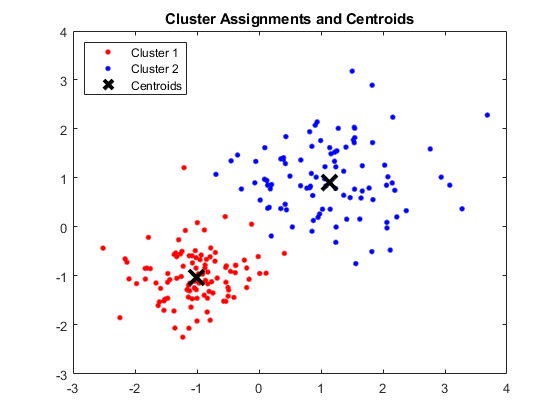
Źródło obrazu

Wyniki:

Otrzymane centroidy są następujące:

1. Wartość X1 i X2 dla Centroid 1: 1.3661; 1,7232
2. Wartość X1 i X2 dla Centroid 2: -1,015; -1,053
3. Wartość X1 i X2 dla Centroid 3: 1,6565; 0,36376
4. Wartość X1 i X2 dla Centroid 4: 0,35134; 0,85358

Niektóre obszary biznesowe, w których można wdrożyć klaster K-Means

Grupowanie K-średnich jest wszechstronnym algorytmem i może być używane w wielu biznesowych przypadkach użycia dla dowolnego rodzaju grupowania. Oto kilka przykładów:

Ø Segregacja behawioralna:

• Podział z wykorzystaniem historii zakupów
• Podział za pomocą działań aplikacji, strony internetowej lub platformy
• Identyfikuj wizerunek klientów na podstawie ich zainteresowań
• Tworzenie profilu z czynnościami monitorującymi

ØSkalowanie obrazu

• Kompresja obrazu przy użyciu Pythona

Ø Pomiary czujnika:

• Wykryj typy aktywności czujników ruchu
• Obrazy grupowe
• Podziel dźwięk
• Grupy monitorowania stanu Spot

Ø Określ boty lub anomalie:

• Oddziel grupy aktywności od botów
• Utwórz grupę prawidłowych działań, aby wyczyścić wykrywanie wartości odstających

Ø Klasyfikacja zapasów:

• Twórz grupy magazynowe według aktywności sprzedażowej
• Twórz grupy magazynowe według metryk produkcyjnych

Zalety klastrowania K-Means

Jest powód, dla którego najlepsi profesjonaliści preferują algorytm grupowania K-Means. Niektóre korzyści, jakie oferuje:

• Jest to szybki, niezawodny i łatwiejszy do zrozumienia algorytm.
• Wydajność końcowa jest stosunkowo wysoka
• Oferuje fenomenalne wyniki, gdy zestawy danych różnią się od siebie. W przypadku wyższych wartości zmiennych K-Means działa stosunkowo szybciej
• Klastry wytworzone za pomocą K-średnich są stosunkowo węższe niż inne metody grupowania.

Musisz przeczytać: typy danych MATLAB

Wniosek

Grupowanie K-średnich jest szeroko stosowanym podejściem do analizy skupień danych. Gdy zdobędziesz kontrolę, łatwiej jest zrozumieć, zastosować i szybko dostarczyć wyniki.

Mamy nadzieję, że z tym artykułem; możemy wprowadzić Cię w tę technikę analizy. W przypadku jakichkolwiek pytań dotyczących algorytmu K-średnich prosimy o komentarz poniżej.

Ponadto, jeśli ta dziedzina Cię interesuje, spójrz na nasz program PG Diploma in Machine Learning and AI , który jest specjalnie wyselekcjonowany dla pracujących profesjonalistów oferujących ponad 30 studiów przypadków i zadań, ponad 25 sesji mentorskich od ekspertów branżowych, 10 praktycznych rąk- w projektach Capstone, ponad 450 godzin pomocy w nauce i stażu.

Co to jest klastrowanie K Means w uczeniu maszynowym?

Jest to popularny algorytm klastrowania używany w nienadzorowanym uczeniu maszynowym. Algorytm K Means działa na zasadzie losowej identyfikacji centroidów K. Od następnego kroku algorytm próbuje zmaksymalizować ogólną odległość między klastrami, a także zminimalizować ogólną odległość między klastrami. Algorytm K Mean jest podejściem iteracyjnym. W każdej iteracji wybiera średnią K z bieżącego zestawu centroidów. Algorytm następnie przypisuje każdą obserwację do najbliższej średniej K. Odległość między dwoma skupiskami jest obliczana na podstawie odległości między dwiema najbliższymi obserwacjami. Centroida klastra jest zdefiniowana jako średnia wszystkich obserwacji w klastrze.

Jakie są ograniczenia algorytmu grupowania K Means?

Istnieją pewne ograniczenia K Means, o których należy pamiętać podczas korzystania z niego. K Means nie jest odporny na wartości odstające. Algorytm K Means działa dobrze tylko wtedy, gdy wszystkie punkty danych znajdują się w przybliżeniu w tej samej odległości od środka ciężkości. Jeśli niektóre z Twoich punktów danych znajdują się daleko od centroidu, spowoduje to obciążenie przypisania innych punktów danych do klastrów. K Means nie gwarantuje unikalnego rozwiązania. Jeśli masz więcej niż jeden klaster punktów, nie ma gwarancji, że K Means zwróci tę samą liczbę klastrów za każdym razem, gdy algorytm zostanie uruchomiony. K Średnie zbiegają się powoli. Algorytm zbiega się bardzo powoli, nawet na małych zbiorach danych.

Jakie są zalety klastrowania K Means?

Jest skuteczny zarówno w przypadku jednego, jak i wielu wymiarów. Ma zastosowanie zarówno w dwóch, jak i trzech wymiarach. Jest to szczególnie przydatne w sytuacjach, gdy istnieje wiele klastrów. Klastry uzyskuje się w środkowym punkcie punktów danych. Dla każdego skupienia obliczana jest wartość średnia. Każdy punkt jest dzielony przez odchylenie standardowe, a następnie porównywany z wartością średnią. Dla wszystkich skupień i punktów oblicza się wartość średnią i odchylenie standardowe.