K Kümeleme Matlab anlamına gelir [Kaynak Kodlu]
Yayınlanan: 2020-12-09K-ortalama kümeleme, veri uzmanları tarafından en sık kullanılan tekniklerden biridir. Algoritmanın etkinliği nedeniyle, çeşitli uygulamalarda çok sayıda endüstri tarafından talep edilmektedir.
Bir veri bilimcisinin işi, birçok aşamada Kümelemenin uygulanmasını gerektirir. Birçok büyük ölçekli proje şu anda kümeleme algoritmasına dayanmaktadır ve veri bilimi uzmanlarının talebi için çıtayı büyük ölçüde yükseltmiştir.
Bu algoritmalardan biri, bu makalenin temel fikri ve MATLAB kaynak koduyla uygulanması olan K-araç kümelemedir.
Konuyu kavramadan önce, Kümelemenin ne olduğuna, önemine ve gerçek hayatta nasıl uygulanabileceğine hızlıca bir göz atalım. Gönderinin sonunda, bu algoritmanın büyük kümelerdeki verileri anlamak için ne kadar önemli olduğunu öğreneceksiniz.
İçindekiler
Kümeleme nedir?
Veri, herhangi bir uygulama için en kritik bileşendir ve bir küme, birleştirilmiş benzer veri noktalarının birikiminden başka bir şey değildir. Adından da anlaşılacağı gibi, Kümeleme, büyük bir veri yığınını alt gruplara veya yalnızca veri modeline dayalı olarak kümelere bölme işlemidir.
Makine öğreniminde, önceden tanımlanmış veri olmadığında Kümeleme uygulanır. Nihai amaç, verileri yüksek sınıf içi benzerliğe sahip sınıflar halinde gruplamaktır.

Kümeleme, verileri keşfetmek için kullanılır. Kullanılabileceği bazı gerçek hayattan örnekler, benzer davranışlara sahip müşterileri bulmak için pazar bölümlendirme, görüntü bölümlendirme/sıkıştırma, birden çok konu ile belge kümeleme vb.
Denetimli modeller oluşturmak için homojen grupları belirlemek için verileri işlemeden önce gerekli bir adımdır. K-Means kümeleme, benzer gözlemleri entegre etmek ve farklı gruplar oluşturmak için veri aramamız gerektiğinden, denetimsiz bir öğrenme algoritmasıdır .
En çok uygulanan ve en basit kümeleme algoritmalarından biri olan K-Means algoritmasına bir göz atalım .
K-Ortalamalar Kümeleme
Görüntü Kaynağı
K-ortalama kümeleme, en çok istenen denetimsiz makine öğrenimi algoritmalarından biridir.
Denetimsiz algoritmalar, etiketlenmiş sonuçlara başvurmadan girdi vektörlerini kullanarak veri kümelerinden sonuçlar çıkarır.
Veri kümesini, her veri noktasının bir gruba ait olduğu Küme içi veri noktalarının benzerliği artırılır ve kümeler arasındaki mesafe optimum tutulur.
Veri noktaları ve kümenin ağırlık merkezi arasındaki mesafe, Öklid mesafesi gibi minimumda tutulur. K-Means'te her küme bir merkeze bağlıdır. Birincil amaç, noktalar ve ilgili küme ağırlık merkezi arasındaki mesafeleri en aza indirmektir.
K-Means Kümeleme Nasıl Çalışır?
Kümeleme işlemi, gerçekleştirilecek birkaç yineleme anlamına geldiğinden, K-Means algoritmasının benzersiz bir çalışma şekli vardır. İşte çalışma şeklinin adım adım açıklaması:
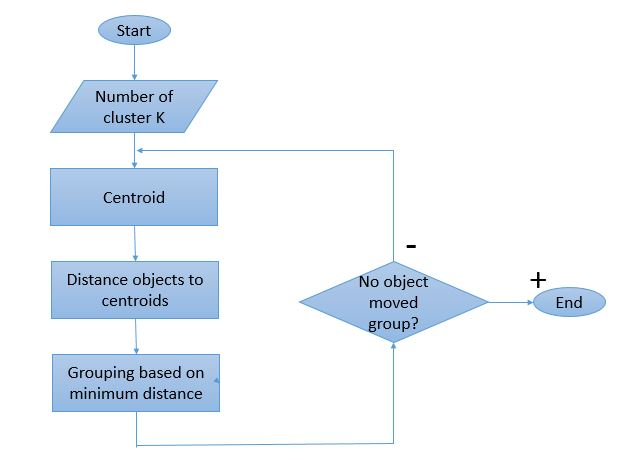
Görüntü Kaynağı
Adım 1: Başlangıçta, ' Adım 2: Her küme için rasgele K veri noktalarını merkezler olarak başlatın.
2 küme varsa, 'K' değeri 2 olacaktır.
Adım 3: Kümelere atanan veri noktaları değişmeyene kadar birkaç yineleme gerçekleştirin.
Adım 4: Veri noktaları ve merkezler arasındaki kare uzaklığın toplamını hesaplayın.
Adım 5: Mesafeyi en aza indirmek için her bir veri noktasını en yakın kümeye (centroid) tahsis edin.
Adım 6: Birbirine ait kümelerin ağırlık merkezlerinin ortalamasını alın.
Bu, ağırlık merkezini hesaplamak ve noktaları merkeze olan uzaklıklarına göre kümeye atamak için gerçekleştirilen tek bir yineleme işlemidir. Tüm merkezler tanımlandıktan sonra işlem durdurulur.
K-Means Kümelemenin Uygulanmasını Gösteren Açıklayıcı Bir Örnek
Açıklama: Ünlü gıda zincirlerinden biri olan McDonald's, California genelinde bir outlet zinciri açmak ve kendilerine maksimum gelir sağlayacak yerleri bulmak istiyor.
McDonald's Zaten Neye Sahip?
Ø Güçlü bir e-ticaret varlığı
Ø Siparişlerin sıklıkla verildiği lokasyonları analiz etmek için çevrimiçi müşteri verileri
Karşılaşabilecekleri olası zorluklar
- Siparişlerin sıklıkla verildiği bölgelerin analiz edilmesi.
- Bölgede kaç tane priz açılacağını kavrayın
- Mağaza ve teslimat noktaları arasında minimum mesafeyi korumak için tüm alanlardaki satış noktalarının yerlerini belirleyin.
Tüm bu noktalar üzerinde çalışmak için çok fazla analiz ve matematik gerekir.
K-araçları Kümeleme Yöntemi burada nasıl kullanılabilir?
Önceden tanımlanmış bir K değeriyle, K-ortalama algoritması aşağıdaki adımlarda uygulanabilir:
- K Nesnelerin K boş olmayan alt kümelere bölünmesi ile mağaza konumlarının belirlenmesi.
- Bölümün küme ağırlık merkezlerini belirleme.
- Her konumu belirli bir kümeye atama.
- Her lokasyondan mesafelerin hesaplanması ve çıkış ile mesafenin minimum olduğu kümeye noktalar tahsis edilir.
- Bir yinelemeden sonra, noktaları yeniden tahsis ederek oluşan yeni kümenin ağırlık merkezini bulun.
Benzer şekilde, K-Means Kümeleme algoritması, çeşitli ölçeklerde çeşitli uygulamalara uygulanabilir. Konaklama endüstrisi, suç soruşturma departmanları ve imajın yeniden boyutlandırılması bunlardan birkaçıdır.
K-Means algoritması R , Python, MATLAB vb. gibi birçok dil kullanılarak uygulanmaktadır . Bir sonraki bölümde K-Means Clustering MATLAB'ın nasıl uygulandığına bakacağız.

Okuyun: Matlab'daki Fonksiyon Türleri
MATLAB Kullanan K-Ortalamalar Algoritması
K-Means, veri bilimi, makine öğrenimi, yapay zeka, kriptografi ve siber güvenlik ile uğraşan birçok profesyonel tarafından kullanılan, büyük ölçüde kullanılan bir algoritmadır.
Bu algoritmayı kullanmanın temel amacı, her kümenin merkezini bulmaktır. Bir programcıya verilen veriler heterojendir. İşte her kümenin ağırlık merkezini çizmek ve her bir merkezin koordinatlarını atamak için MATLAB kodu:
Kümeleme MATLAB
Kod:
rng varsayılanı; % Tekrarlanabilirlik için
X = [randn(100,2)*0.75+birler(100,2);
randn(100,2)*0.5-bir(100,2)];
opts=statset('Görüntüleme','son');
[idx,C]=kmeans(X,4,'Distance','cityblock','Replicates',5,'Options',opts);
plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12);
devam etmek;
plot(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12);
plot(X(idx==3,1),X(idx==3,2),'g.','MarkerSize',12);
plot(X(idx==4,1),X(idx==4,2),'y.','MarkerSize',12);
arsa(C(:,1),C(:,2),'Kx','MarkerSize',15,'LineWidth',3);
legend('Cluster 1','Cluster 2','Cluster 3','Cluster 4','Centroids', 'Location','NW');
title('Küme Atamaları ve merkezleri');
uzak dur;
i=1 için:boyut(C, 1)
display(['Centroid', num2str(i), ': X1 = ', num2str(C(i, 1)), '; X2 = ', num2str(C(i, 2))]);
son
Çıktı:
Dört Küme ve İlgili Merkezleri Gösteren MATLAB Penceresi
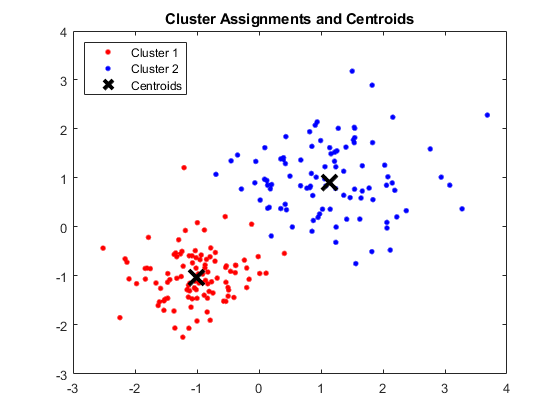
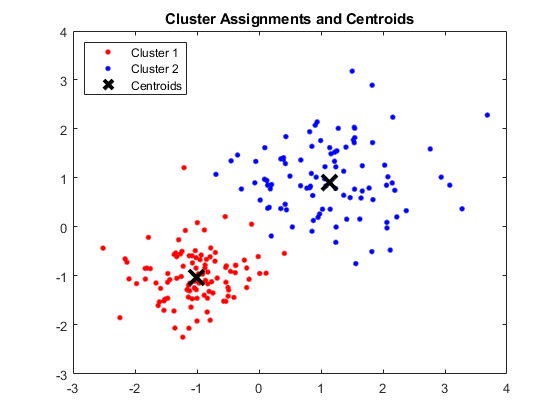
Görüntü Kaynağı
Sonuçlar:
Elde edilen centroidler aşağıdaki gibidir:
- Centroid 1: 1.3661 için X1 & X2 değeri; 1.7232
- Centroid 2 için X1 & X2 değeri: -1.015; -1.053
- Centroid 3: 1.6565 için X1 & X2 değeri; 0.36376
- Centroid 4 için X1 & X2 değeri: 0.35134; 0.85358
K-Means kümelemesinin uygulanabileceği bazı iş alanları
K-ortalama kümeleme, çok yönlü bir algoritmadır ve her tür gruplama için birçok iş kullanım durumu için kullanılabilir. Bazı örnekler:
Ø Davranış Ayrımı:
- Satın alma geçmişini kullanan bölüm
- Uygulama, web sitesi veya platform etkinliklerini kullanarak bölme
- Müşterilerin imajını ilgi alanlarına göre belirleyin
- İzleme faaliyetleri ile profil oluşturma
Ø Görüntü Ölçekleme
- Python kullanarak görüntü sıkıştırma
Ø Sensör ölçümleri:
- Hareket sensörleri aktivite türlerini tespit edin
- Grup resimleri
- Sesi böl
- Spot sağlık izleme grupları
Ø Botları veya anormallikleri belirleyin:
- Botlardan ayrı aktivite grupları
- Aykırı değer algılamasını temizlemek için bir grup geçerli etkinlik yapın
Ø Envanter sınıflandırması:

- Satış etkinliğine göre envanter grupları oluşturun
- Üretim metriklerine göre envanter grupları oluşturun
K-Means Kümelemenin Avantajları
En iyi profesyonellerin K-Means kümeleme algoritmasını tercih etmelerinin bir nedeni var. Sunduğu bazı avantajlar:
- Hızlı, sağlam ve anlaşılması daha kolay bir algoritmadır.
- Nihai verimlilik nispeten yüksektir
- Veri kümeleri birbirinden farklı olduğunda olağanüstü sonuçlar sunar. Daha yüksek değişken değerleri için K-Means nispeten daha hızlı çalışır
- K-Means ile üretilen kümeler, diğer kümeleme yöntemlerinden nispeten daha sıkıdır.
Okunması Gerekenler: MATLAB Veri Tipleri
Çözüm
K-ortalama kümeleme, veri kümelerini analiz etmek için yaygın olarak kullanılan bir yaklaşımdır. Komuta kazandığınızda, anlamak ve uygulamak ve sonuçları hızlı bir şekilde iletmek daha kolaydır.
Bu makale ile umarız; sizi bu analiz tekniğiyle tanıştırabiliriz. K-araç algoritması ile ilgili herhangi bir sorgu için aşağıya yorum yapmaktan çekinmeyin.
Ayrıca, bu çalışma alanı ilginizi çekiyorsa, 30'dan fazla vaka çalışması ve ödev, endüstri uzmanlarından 25'ten fazla mentorluk oturumu, 10 Pratik El- Capstone Projelerinde, 450+ saat öğrenme ve yerleştirme yardımı.
K, makine öğreniminde kümeleme anlamına gelir?
Bu, denetimsiz makine öğreniminde kullanılan popüler bir kümeleme algoritmasıdır. K Means algoritması, K centroidlerinin rastgele tanımlanması prensibi ile çalışır. Bir sonraki adımdan itibaren, algoritma küme içindeki toplam mesafeyi maksimize etmeye ve ayrıca kümeler arasındaki toplam mesafeyi minimize etmeye çalışır. K Means algoritması yinelemeli bir yaklaşımdır. Her yinelemede, geçerli merkez kümesinden K Ortalamasını seçer. Algoritma daha sonra her bir gözlemi en yakın K Ortalamasına atar. İki küme arasındaki mesafe, en yakın iki gözlem arasındaki mesafeye göre hesaplanır. Bir kümenin Centroid'i, kümedeki tüm gözlemlerin ortalaması olarak tanımlanır.
K Means kümeleme algoritmasının sınırlamaları nelerdir?
K Means'i kullanırken aklınızda bulundurmak isteyeceğiniz bazı sınırlamalar vardır. K Means, aykırı değerlere karşı dayanıklı değildir. K Means algoritması, yalnızca tüm veri noktalarınız merkezden yaklaşık olarak aynı uzaklıkta olduğunda iyi çalışır. Veri noktalarınızdan bazıları merkezden uzaktaysa, bu, diğer veri noktalarının kümelere atanmasını saptıracaktır. K Means benzersiz bir çözümü garanti etmez. Birden fazla nokta kümeniz varsa, algoritma her çalıştırıldığında K Means'in aynı sayıda kümeyi döndüreceğinin garantisi yoktur. K Yavaş yakınsayan anlamına gelir. Algoritma, küçük veri kümelerinde bile çok yavaş yakınsar.
K Means kümelemenin avantajları nelerdir?
Hem tek hem de çoklu boyutlar için etkilidir. Hem iki hem de üç boyutta uygulanabilir. Özellikle çok sayıda kümenin olduğu durumlarda kullanışlıdır. Kümeler, veri noktalarının orta noktasında elde edilir. Her küme için ortalama bir değer hesaplanır. Her nokta standart sapmaya bölünür ve ardından ortalama değerle karşılaştırılır. Tüm kümeler ve noktalar için ortalama değer ve standart sapma hesaplanır.
