K означает кластеризацию Matlab [с исходным кодом]
Опубликовано: 2020-12-09Кластеризация K-средних является одним из наиболее часто используемых методов профессионалами в области данных. Благодаря эффективности алгоритма он востребован многими отраслями в различных приложениях.
Работа специалиста по данным требует реализации кластеризации на многих этапах. Многие крупномасштабные проекты в настоящее время основаны на алгоритме кластеризации и резко подняли планку требований специалистов по науке о данных.
Одним из таких алгоритмов является кластеризация K-средних, которая является основной идеей этой статьи и ее реализацией с помощью исходного кода MATLAB.
Прежде чем перейти к теме, давайте кратко рассмотрим, что такое кластеризация, ее значение и то, как ее можно реализовать в реальной жизни. К концу поста вы узнаете, насколько важен этот алгоритм для понимания данных в больших наборах.
Оглавление
Что такое кластеризация?
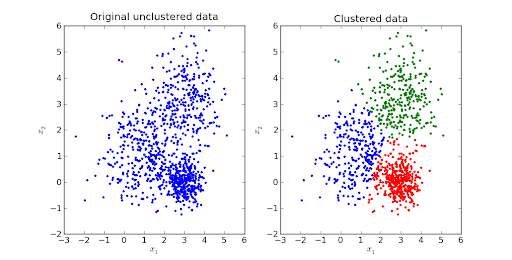
Данные являются наиболее важным компонентом для любого приложения, а кластер представляет собой не что иное, как совокупность схожих точек данных. Как ясно из названия, кластеризация — это процесс разделения большого куска данных на подгруппы или только кластеры на основе шаблона данных.
В машинном обучении кластеризация применяется, когда нет доступных предопределенных данных. Конечная цель состоит в том, чтобы сгруппировать данные в классы с высоким внутриклассовым сходством.

Кластеризация используется для изучения данных. Некоторые примеры из реальной жизни, где его можно использовать, включают сегментацию рынка для поиска клиентов со схожим поведением, сегментацию/сжатие изображений, кластеризацию документов по нескольким темам и т. д.
Перед обработкой данных необходимо определить однородные группы для построения контролируемых моделей. Кластеризация K-средних — это алгоритм обучения без учителя, поскольку нам нужно искать данные, чтобы интегрировать аналогичные наблюдения и формировать отдельные группы.
Давайте взглянем на алгоритм K-средних , который является одним из наиболее применяемых и самых простых алгоритмов кластеризации.
Кластеризация K-средних
Источник изображения
Кластеризация K-средних — один из самых желанных алгоритмов машинного обучения без учителя.
Неконтролируемые алгоритмы делают выводы из наборов данных, используя входные векторы, не обращаясь к помеченным результатам.
Это итеративный алгоритм на основе расстояния или центроида, который разделяет набор данных на K отдельных подгрупп (кластеров), где каждая точка данных принадлежит одной группе . Подобие точек данных внутри кластера увеличивается, а расстояние между кластерами поддерживается оптимальным.
Расстояние между точками данных и центроидом кластера сохраняется на минимальном уровне, таком как евклидово расстояние. В K-Means каждый кластер связан с центроидом. Основная цель состоит в том, чтобы минимизировать расстояния между точками и центроидом соответствующего кластера.
Как работает кластеризация K-средних?
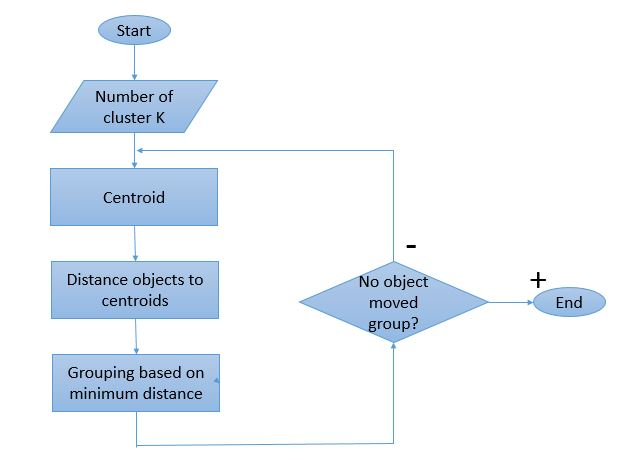
Поскольку процесс кластеризации означает выполнение нескольких итераций, алгоритм K-Means имеет уникальный способ работы. Вот пошаговое объяснение того, как это работает:
Источник изображения
Шаг 1: Первоначально определите количество кластеров « Шаг 2: Инициализируйте случайные точки данных K как центроиды для каждого кластера.
Если есть 2 кластера, значение «K» будет равно 2.
Шаг 3: Выполните несколько итераций, пока назначенные точки данных для кластеров не изменятся.
Шаг 4: Рассчитайте сумму квадратов расстояний между точками данных и центроидами.
Шаг 5: Распределите каждую точку данных по ближайшему кластеру (центроиду), чтобы минимизировать расстояние.
Шаг 6: Возьмите среднее значение центроидов кластеров, принадлежащих друг другу.
Это один итерационный процесс, выполняемый для вычисления центроида и назначения точек кластеру на основе их расстояния от центроида. Как только все центроиды определены, процесс останавливается.
Иллюстративный пример, изображающий реализацию кластеризации K-средних
Заявление: McDonald's, одна из известных сетей общественного питания, хочет открыть сеть торговых точек по всей Калифорнии и найти места, которые принесут ей максимальный доход.
Что у McDonald's уже есть?
Ø Сильное присутствие в электронной коммерции
Ø Онлайн-данные о клиентах для анализа мест, откуда часто делаются заказы
Возможные проблемы, с которыми они могут столкнуться
- Анализ областей, откуда чаще всего делаются заказы.
- Понять, сколько торговых точек нужно открыть в районе
- Определите расположение торговых точек во всех районах, чтобы сохранить минимальное расстояние между магазином и пунктами доставки.
Все эти моменты требуют большого анализа и математики для работы.
Как здесь можно использовать метод кластеризации K-средних?
С предопределенным значением K алгоритм K-средних может быть реализован в следующих шагах:
- Идентификация местоположений магазинов с помощью K Разделение объектов на K непустых подмножеств.
- Определение центроидов кластера раздела.
- Присвоение каждой локации определенному кластеру.
- Вычисление расстояний от каждого местоположения и выделение точек кластеру, где расстояние до выхода минимально.
- После одной итерации, перераспределяя точки, найдите центр тяжести нового образовавшегося кластера.
Точно так же алгоритм кластеризации K-средних можно применять к множеству приложений в различных масштабах. Индустрия гостеприимства, отделы по расследованию преступлений и изменение размера изображений, и это лишь некоторые из них.

Алгоритм K-Means реализован с использованием многих языков, таких как R , Python, MATLAB и т. д. В следующем разделе мы рассмотрим, как применяется K-Means Clustering MATLAB.
Читайте: Типы функций в Matlab
Алгоритм K-средних Используя MATLAB
K-Means — широко используемый алгоритм, используемый многими профессионалами, занимающимися наукой о данных, машинным обучением, искусственным интеллектом, криптографией и кибербезопасностью.
Основная цель использования этого алгоритма — найти центр тяжести каждого кластера. Данные, предоставляемые программисту, неоднородны. Вот код MATLAB для построения центроида каждого кластера и назначения координат каждого центроида:
Кластеризация MATLAB
Код:
по умолчанию; % Для воспроизводимости
X = [рандn(100,2)*0,75+единицы(100,2);
randn(100,2)*0,5-единиц(100,2)];
opts=statset('Показать','финал');
[idx,C]=kmeans(X,4,'Расстояние','городской квартал','Репликаты',5,'Опции',opts);
plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12);
Подожди;
plot(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12);
plot(X(idx==3,1),X(idx==3,2),'g.','MarkerSize',12);
plot(X(idx==4,1),X(idx==4,2),'y.','MarkerSize',12);
plot(C(:,1),C(:,2),'Kx','MarkerSize',15,'LineWidth',3);
легенда («Кластер 1», «Кластер 2», «Кластер 3», «Кластер 4», «Центроиды», «Местоположение», «СЗ»);
title('Назначения кластеров и центроиды');
откладывать;
для я = 1: размер (С, 1)
display(['Centroid ', num2str(i), ': X1 = ', num2str(C(i, 1)), '; X2 = ', num2str(C(i, 2))]);
конец
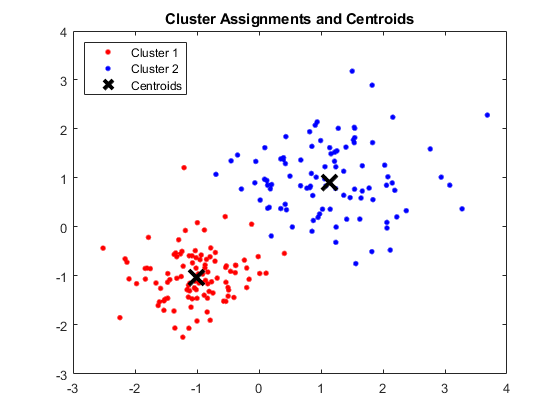
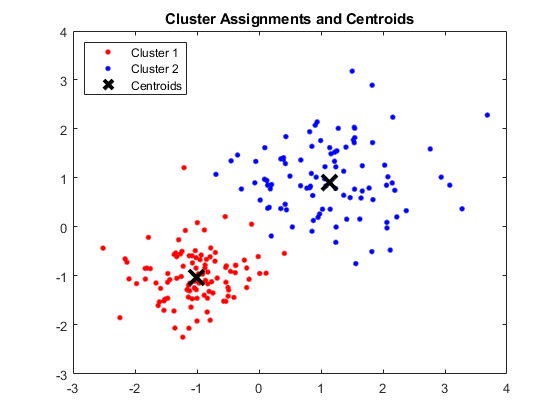
Выход:
Окно MATLAB, показывающее четыре кластера и соответствующие центроиды
Источник изображения
Результаты:
Полученные центроиды следующие:
- Значение X1 и X2 для центроида 1: 1,3661; 1,7232
- Значение X1 и X2 для центроида 2: -1,015; -1,053
- Значение X1 и X2 для Centroid 3: 1,6565; 0,36376
- Значение X1 и X2 для Centroid 4: 0,35134; 0,85358
Некоторые области бизнеса, в которых может быть реализована кластеризация K-средних
Кластеризация K-средних — это универсальный алгоритм, который можно использовать для многих бизнес-применений для любого типа группировки. Некоторые примеры:
Ø Поведенческая сегрегация:
- Разделение с использованием истории покупок
- Разделение с использованием приложения, веб-сайта или платформы
- Определение имиджа клиентов на основе их интересов
- Создание профиля с мониторингом действий
Ø Масштабирование изображения
- Сжатие изображений с использованием Python
Ø Измерения датчика:
- Обнаружение типов активности датчиков движения
- Групповые изображения
- Разделить аудио
- Спотовые группы мониторинга здоровья
Ø Определите ботов или аномалии:
- Отдельные группы активности от ботов
- Создайте группу допустимых действий, чтобы очистить обнаружение выбросов
Ø Инвентарная классификация:

- Сгруппируйте запасы по активности продаж
- Создавайте группы запасов по производственным показателям
Преимущества кластеризации K-средних
Есть причина, по которой ведущие профессионалы предпочитают алгоритм кластеризации K-Means. Некоторые преимущества, которые он предлагает:
- Это быстрый, надежный и простой для понимания алгоритм.
- Конечная эффективность относительно высока
- Предлагает феноменальные результаты, когда наборы данных отличаются друг от друга. Для более высоких значений переменных K-Means работает сравнительно быстрее.
- Кластеры, созданные с помощью K-средних, относительно плотнее, чем другие методы кластеризации.
Обязательно прочтите: Типы данных MATLAB
Заключение
Кластеризация K-средних — это широко используемый подход для анализа кластеров данных. Как только вы овладеете навыками, их будет легче понять, применять и быстро получать результаты.
Мы надеемся с этой статьей; мы могли бы познакомить вас с этой техникой анализа. По любым вопросам, касающимся алгоритма K-средних, не стесняйтесь комментировать ниже.
Кроме того, если эта область обучения вас интересует, взгляните на нашу программу диплома PG в области машинного обучения и искусственного интеллекта , которая специально разработана для работающих профессионалов, предлагая более 30 тематических исследований и заданий, более 25 наставнических занятий от отраслевых экспертов, 10 практических рук. на Capstone Projects, более 450 часов обучения и помощи в трудоустройстве.
Что такое кластеризация K Means в машинном обучении?
Это популярный алгоритм кластеризации, используемый в неконтролируемом машинном обучении. Алгоритм K-средних работает по принципу случайной идентификации K центроидов. На следующем этапе алгоритм пытается максимизировать общее расстояние внутри кластера, а также минимизировать общее расстояние между кластерами. Алгоритм K-средних представляет собой итеративный подход. На каждой итерации он выбирает K средних значений из текущего набора центроидов. Затем алгоритм присваивает каждому наблюдению ближайшее значение K Mean. Расстояние между двумя кластерами вычисляется на основе расстояния между двумя ближайшими наблюдениями. Центроид кластера определяется как среднее значение всех наблюдений в кластере.
Каковы ограничения алгоритма кластеризации K-средних?
Существуют некоторые ограничения K-средств, которые вы должны иметь в виду при его использовании. K Среднее не является устойчивым к выбросам. Алгоритм K-средних работает хорошо только тогда, когда все ваши точки данных находятся примерно на одинаковом расстоянии от центроида. Если некоторые из ваших точек данных находятся далеко от центроида, это приведет к смещению присвоения других точек данных кластерам. K Means не гарантирует уникальность решения. Если у вас более одного кластера точек, нет гарантии, что K-средние будут возвращать одно и то же количество кластеров при каждом запуске алгоритма. K Значит медленно сходится. Алгоритм сходится очень медленно, даже на небольших наборах данных.
Каковы преимущества кластеризации K Means?
Он эффективен как для одного, так и для нескольких измерений. Он применим как в двух, так и в трех измерениях. Это особенно полезно в ситуациях, когда имеется много кластеров. Кластеры получаются в средней точке точек данных. Среднее значение рассчитывается для каждого кластера. Каждая точка делится на стандартное отклонение, а затем сравнивается со средним значением. Среднее значение и стандартное отклонение рассчитываются для всех кластеров и точек.
