K 表示聚類 Matlab [附源碼]
已發表: 2020-12-09K-means 聚類是數據專業人員最常用的技術之一。 由於算法的有效性,它在各種應用中受到眾多行業的需求。
數據科學家的工作需要在多個階段實施聚類。 目前許多大型項目都基於聚類算法,大大提高了對數據科學專業人士的需求。
其中一種算法是 K-means 聚類,這是本文的基本思想及其在 MATLAB 源代碼中的實現。
在抓住主題之前,讓我們快速了解一下集群是什麼、它的意義以及如何在現實生活中實現它。 在這篇文章的最後,您將了解該算法對於理解大型數據集的重要性。
目錄
什麼是聚類?
數據是任何應用程序最關鍵的組成部分,而集群只不過是相似數據點的組合。 顧名思義,聚類是根據數據模式將大量數據劃分為子組或僅聚類的過程。
在機器學習中,當沒有可用的預定義數據時應用聚類。 最終目的是將數據分組到具有高類內相似性的類中。

聚類用於探索數據。 可以使用它的一些現實示例是市場細分以找到具有相似行為的客戶、圖像分割/壓縮、具有多個主題的文檔聚類等。
這是處理數據以識別同質組以構建監督模型之前的必要步驟。 K-Means 聚類是一種無監督學習算法,因為我們必須尋找數據來整合相似的觀察結果並形成不同的組。
我們來看看K-Means算法,它是應用最多、最簡單的聚類算法之一。
K-Means 聚類
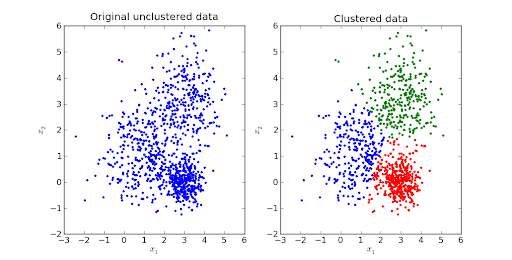
圖片來源
K-means 聚類是最受歡迎的無監督機器學習算法之一。
無監督算法使用輸入向量從數據集中得出結論,而不參考標記結果。
它是一種基於迭代距離或基於質心的算法,將數據集分成K個不同的子組(簇),其中每個數據點屬於一個組。 增加了簇內數據點的相似度,使簇之間的距離保持最佳。
數據點與簇質心之間的距離保持在最小值,例如歐幾里得距離。 在 K-Means 中,每個簇都鏈接到一個質心。 主要目的是最小化點與各自簇質心之間的距離。
K-Means 聚類如何工作?
由於聚類過程意味著要執行多次迭代,因此 K-Means 算法具有獨特的工作方式。 以下是其工作方式的分步說明:
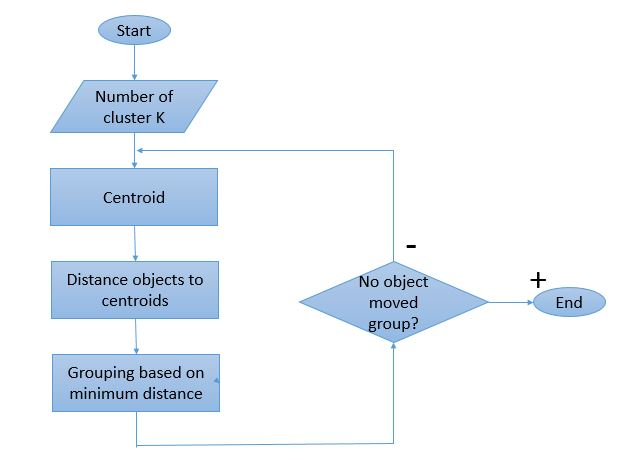
圖片來源
第 1 步:最初,定義集群的數量“ 第 2 步:將隨機 K 個數據點初始化為每個集群的質心。
如果有 2 個簇,則“K”的值為 2。
第 3 步:執行多次迭代,直到分配給集群的數據點不變。
第 4 步:計算數據點與質心之間的平方距離之和。
步驟 5:將每個數據點分配到最近的集群(質心)以最小化距離。
第 6 步:取屬於彼此的簇的質心的平均值。
這是一個單次迭代過程,用於計算質心並根據它們與質心的距離將點分配給集群。 一旦定義了所有質心,該過程就會停止。
描述 K-Means 聚類實現的示例
聲明:作為著名的食品連鎖店之一,麥當勞希望在加州開設連鎖店,並希望找出能為他們帶來最大收入的地點。
麥當勞已經有什麼?
Ø 強大的電子商務存在
Ø 在線客戶數據,用於分析頻繁下單的地點
他們可能面臨的挑戰
- 分析頻繁下單的區域。
- 了解該地區將開設多少家門店
- 找出所有區域內的網點位置,以保持商店和送貨點之間的最小距離。
所有這些點都需要大量的分析和數學來研究。
這裡如何使用 K-means 聚類方法?
使用預定義的 K 值,可以通過以下步驟實現 K-means 算法:
- 用 K 個對象劃分為 K 個非空子集來識別商店位置。
- 確定分區的簇質心。
- 將每個位置分配給特定集群。
- 計算與每個位置的距離,並將點分配給與出口距離最小的集群。
- 經過一次迭代,重新分配點,找到形成的新簇的質心。
同樣,K-Means 聚類算法可以應用於各種規模的各種應用。 酒店業、犯罪調查部門和圖像大小調整等等。
K-Means 算法使用 R 、Python、MATLAB 等多種語言實現。在下一節中,我們將看看 K-Means Clustering MATLAB 是如何應用的。
閱讀: Matlab 中的函數類型
使用 MATLAB 的 K-Means 算法
K-Means 是許多處理數據科學、機器學習、人工智能、密碼學和網絡安全的專業人士廣泛使用的算法。

使用該算法的核心目標是找出每個簇的質心。 給程序員的數據是異構的。 這是繪製每個集群的質心並分配每個質心的坐標的 MATLAB 代碼:
聚類 MATLAB
代碼:
rng 默認; % 再現性
X = [randn(100,2)*0.75+ones(100,2);
randn(100,2)*0.5-ones(100,2)];
opts=statset('顯示','final');
[idx,C]=kmeans(X,4,'Distance','cityblock','Replicates',5,'Options',opts);
plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12);
堅持,稍等;
plot(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12);
plot(X(idx==3,1),X(idx==3,2),'g.','MarkerSize',12);
plot(X(idx==4,1),X(idx==4,2),'y.','MarkerSize',12);
plot(C(:,1),C(:,2),'Kx','MarkerSize',15,'LineWidth',3);
legend('Cluster 1','Cluster 2','Cluster 3','Cluster 4','Centroids','Location','NW');
title('聚類分配和質心');
暫緩;
對於 i=1:size(C, 1)
display(['質心', num2str(i), ': X1 = ', num2str(C(i, 1)), '; X2 = ', num2str(C(i, 2))]);
結尾
輸出:
顯示四個聚類和各自質心的 MATLAB 窗口
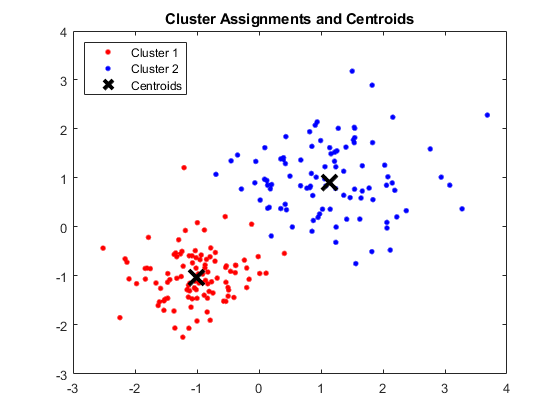
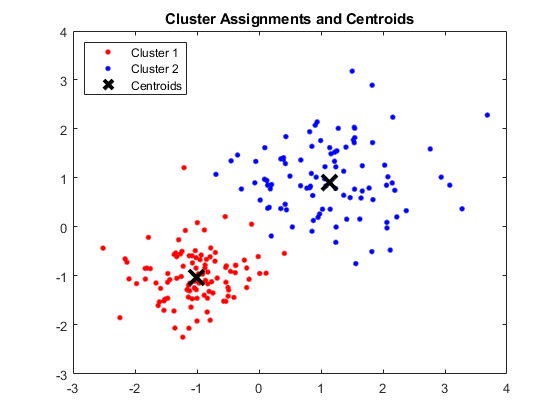
圖片來源
結果:
得到的質心如下:
- 質心 1 的 X1 和 X2 的值:1.3661; 1.7232
- 質心 2 的 X1 和 X2 的值:-1.015; -1.053
- 質心 3 的 X1 和 X2 的值:1.6565; 0.36376
- 質心 4 的 X1 和 X2 的值:0.35134; 0.85358
可以實現 K-Means 聚類的一些業務領域
K-means 聚類是一種通用算法,可用於任何類型的分組的許多業務用例。 一些例子是:
Ø 行為隔離:
- 使用購買歷史的劃分
- 使用應用程序、網站或平台活動的部門
- 根據客戶的興趣識別客戶的形象
- 使用監控活動創建配置文件
Ø 圖像縮放
- 使用 Python 進行圖像壓縮
Ø 傳感器測量:
- 檢測運動傳感器活動類型
- 組圖像
- 分割音頻
- 現場健康監測組
Ø 確定機器人或異常:
- 將活動組與機器人分開
- 做一組有效的活動來清理異常值檢測
Ø 庫存分類:

- 按銷售活動製作庫存組
- 按製造指標製作庫存組
K-Means 聚類的優點
頂級專業人士偏愛 K-Means 聚類算法是有原因的。 它提供的一些好處:
- 它是一種快速、健壯且更易於理解的算法。
- 終端效率比較高
- 當數據集彼此不同時提供驚人的結果。 對於更高的變量值,K-Means 的工作速度相對更快
- 使用 K-Means 生成的聚類比其他聚類方法更緊密。
必讀: MATLAB 數據類型
結論
K-means 聚類是一種廣泛使用的數據聚類分析方法。 一旦你掌握了指揮權,就更容易理解、應用和快速交付結果。
我們希望這篇文章; 我們可以向您介紹這種分析技術。 有關 K-means 算法的任何疑問,請隨時在下面發表評論。
此外,如果您對該研究領域感興趣,請查看我們的機器學習和人工智能 PG 文憑課程,該課程專為在職專業人士提供 30 多個案例研究和作業、25 多個行業專家的指導課程、10 個實踐手-在 Capstone 項目上,450 多個小時的學習和安置幫助。
什麼是機器學習中的 K 均值聚類?
這是一種用於無監督機器學習的流行聚類算法。 K Means 算法的工作原理是隨機識別 K 個質心。 從下一步開始,該算法嘗試最大化總體內簇距離並最小化總體簇間距離。 K 均值算法是一種迭代方法。 在每次迭代中,它從當前的質心集中選擇 K 均值。 然後,該算法將每個觀測值分配給最接近的 K 均值。 兩個聚類之間的距離是根據兩個最接近的觀測值之間的距離計算的。 簇的質心定義為簇中所有觀測值的平均值。
K 均值聚類算法的局限性是什麼?
K 均值有一些限制,您在使用它時需要牢記。 K 均值對異常值不穩健。 僅當所有數據點與質心的距離大致相同時,K 均值算法才有效。 如果您的一些數據點遠離質心,這會使其他數據點分配給集群。 K 均值不保證唯一的解決方案。 如果您有多個點集群,則無法保證每次運行算法時 K 均值都會返回相同數量的集群。 K 均值收斂緩慢。 該算法收斂速度非常慢,即使在小數據集上也是如此。
K 均值聚類的優點是什麼?
它對單維和多維都有效。 它適用於二維和三維。 它在有許多集群的情況下特別有用。 聚類是在數據點的中點獲得的。 為每個集群計算平均值。 每個點除以標準偏差,然後與平均值進行比較。 計算所有簇和點的平均值和標準差。
