K Means ClusteringMatlab[ソースコード付き]
公開: 2020-12-09K-meansクラスタリングは、データの専門家が最も一般的に使用する手法の1つです。 アルゴリズムの有効性により、さまざまなアプリケーションで多くの業界から要求されています。
データサイエンティストの仕事では、多くの段階でクラスタリングを実装する必要があります。 現在、多くの大規模プロジェクトはクラスタリングアルゴリズムに基づいており、データサイエンスの専門家の需要の水準を大幅に引き上げています。
それらのアルゴリズムの1つは、K-meansクラスタリングです。これは、この記事の基本的な考え方と、MATLABソースコードを使用した実装です。
トピックを理解する前に、クラスタリングとは何か、その重要性、および実際の生活でどのように実装できるかを簡単に見てみましょう。 投稿の終わりまでに、このアルゴリズムが大規模なセットのデータを理解するためにどれほど重要であるかがわかるようになります。
目次
クラスタリングとは何ですか?
データはどのアプリケーションにとっても最も重要なコンポーネントであり、クラスターは類似したデータポイントを組み合わせたものに他なりません。 名前が明確に定義しているように、クラスタリングは、データの大きなチャンクをサブグループに分割するプロセス、またはデータパターンに基づいてクラスターのみに分割するプロセスです。
機械学習では、事前定義されたデータが利用できない場合にクラスタリングが適用されます。 最終的な目的は、クラス内の類似性が高いクラスにデータをグループ化することです。

クラスタリングは、データの探索に使用されます。 これを使用できる実際の例としては、同様の動作をする顧客を見つけるための市場セグメンテーション、画像のセグメンテーション/圧縮、複数のトピックを含むドキュメントのクラスタリングなどがあります。
監視ありモデルを構築するための同種のグループを識別するために、データを処理する前に必要な手順です。 K-Meansクラスタリングは、類似した観測値を統合して別個のグループを形成するためのデータを探す必要があるため、教師なし学習アルゴリズムです。
最も適用され、最も単純なクラスタリングアルゴリズムの1つであるK-Meansアルゴリズムを見てみましょう。
K-Meansクラスタリング
画像ソース
K-meansクラスタリングは、最も望ましい教師なし機械学習アルゴリズムの1つです。
教師なしアルゴリズムは、ラベル付けされた結果を参照せずに、入力ベクトルを使用してデータセットから結論を出します。
これは、データセットをK個の異なるサブグループ(クラスター)に分離する反復距離ベースまたは重心ベースのアルゴリズムであり、各データポイントは1つのグループに属します。 クラスター内のデータポイントの類似性が高まり、クラスター間の距離が最適に保たれます。
データポイントとクラスターの重心の間の距離は、ユークリッド距離など、最小に保たれます。 K-Meansでは、各クラスターは重心にリンクされています。 主な目的は、ポイントとそれぞれのクラスター重心の間の距離を最小化することです。
K-Meansクラスタリングはどのように機能しますか?
クラスタリングプロセスは複数の反復を実行することを意味するため、K-Meansアルゴリズムには独自の動作方法があります。 これがその仕組みの段階的な説明です:
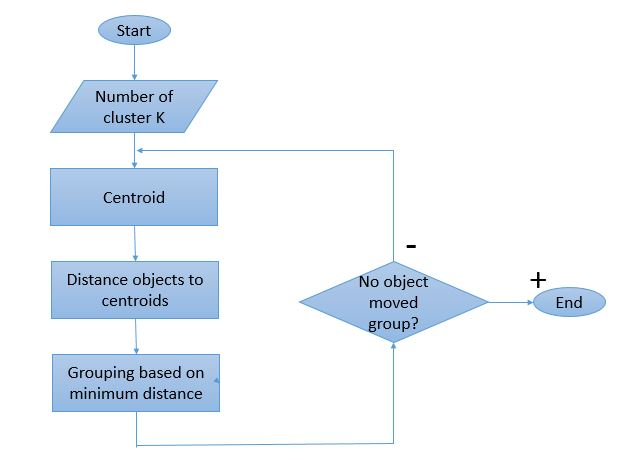
画像ソース
ステップ1:最初に、クラスターの数' ステップ2:各クラスターの重心としてランダムなKデータポイントを初期化します。
クラスターが2つある場合、「K」の値は2になります。
ステップ3:クラスターに割り当てられたデータポイントが変更されなくなるまで、数回の反復を実行します。
ステップ4:データポイントと重心の間の距離の2乗の合計を計算します。
ステップ5:距離を最小化するために、各データポイントを最も近いクラスター(重心)に割り当てます。
ステップ6:互いに属するクラスターの重心の平均を取ります。
これは、重心を計算し、重心からの距離に基づいてポイントをクラスターに割り当てるために実行される単一の反復プロセスです。 すべての図心が定義されると、プロセスは停止します。
K-Meansクラスタリングの実装を示す実例
声明:有名な食物連鎖の1つであるマクドナルドは、カリフォルニア全体に店舗のチェーンを開設し、最大の収益を得る場所を見つけたいと考えています。
マクドナルドはすでに何を持っていますか?
Ø強力なeコマースプレゼンス
Ø注文が頻繁に行われる場所を分析するためのオンライン顧客データ
彼らが直面する可能性のある課題
- 注文が頻繁に行われるエリアを分析します。
- その地域にいくつの店舗を開くかを理解する
- 店舗と配達ポイントの間の最小距離を維持するために、すべてのエリア内のアウトレットの場所を把握します。
これらすべての点に取り組むには、多くの分析と数学が必要です。
ここでK-meansクラスタリング法をどのように使用できますか?
Kの事前定義された値を使用すると、K-meansアルゴリズムを次の手順で実装できます。
- オブジェクトをK個の空でないサブセットに分割することで店舗の場所を特定します。
- パーティションのクラスター重心を決定します。
- 各場所を特定のクラスターに割り当てます。
- 各場所からの距離を計算し、コンセントとの距離が最小になるクラスターにポイントを割り当てます。
- 1回の反復の後、ポイントを再割り当てし、形成された新しいクラスターの重心を見つけます。
同様に、K-Meansクラスタリングアルゴリズムは、さまざまな規模のさまざまなアプリケーションに適用できます。 いくつか例を挙げると、ホスピタリティ業界、犯罪捜査部門、画像のサイズ変更などです。
K-Meansアルゴリズムは、R 、Python、MATLABなどの多くの言語を使用して実装されます。次のセクションでは、K-MeansクラスタリングMATLABがどのように適用されるかを見ていきます。

読む: Matlabの関数の種類
MATLABを使用したK-Meansアルゴリズム
K-Meansは、データサイエンス、機械学習、人工知能、暗号化、サイバーセキュリティを扱う多くの専門家によって広く使用されているアルゴリズムです。
このアルゴリズムを使用する主な目的は、各クラスターの重心を見つけることです。 プログラマーに提供されるデータは異種です。 各クラスターの重心をプロットし、各重心の座標を割り当てるためのMATLABコードは次のとおりです。
クラスタリングMATLAB
コード:
rngデフォルト; %再現性について
X = [randn(100,2)* 0.75 + ones(100,2);
randn(100,2)* 0.5-ones(100,2)];
opts = statset('Display'、'final');
[idx、C] = kmeans(X、4、'Distance'、'cityblock'、'Replicates'、5、'Options'、opts);
plot(X(idx == 1,1)、X(idx == 1,2)、'r。'、'MarkerSize'、12);
持続する;
plot(X(idx == 2,1)、X(idx == 2,2)、'b。'、'MarkerSize'、12);
plot(X(idx == 3,1)、X(idx == 3,2)、'g。'、'MarkerSize'、12);
plot(X(idx == 4,1)、X(idx == 4,2)、'y。'、'MarkerSize'、12);
plot(C(:、1)、C(:、2)、'Kx'、'MarkerSize'、15、'LineWidth'、3);
legend('Cluster 1'、'Cluster 2'、'Cluster 3'、'Cluster 4'、'Centroids'、'Location'、'NW');
title('クラスターの割り当てと重心');
延期します。
i = 1の場合:size(C、1)
display(['Centroid'、num2str(i)、':X1 ='、num2str(C(i、1))、'; X2 ='、num2str(C(i、2))]);
終わり
出力:
4つのクラスターとそれぞれの重心を表示するMATLABウィンドウ
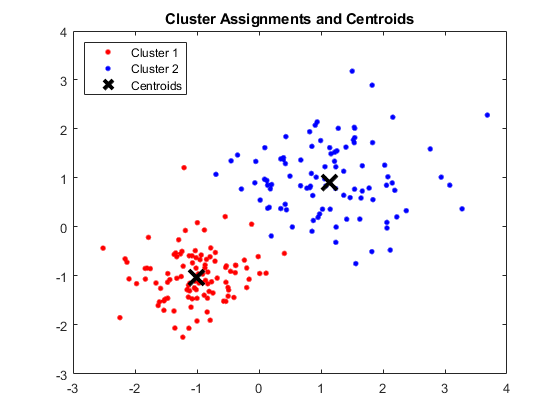
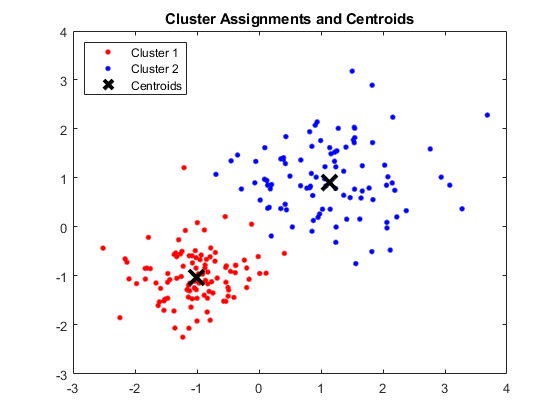
画像ソース
結果:
得られた重心は次のとおりです。
- Centroid 1のX1とX2の値:1.3661; 1.7232
- Centroid 2のX1とX2の値:-1.015; -1.053
- Centroid 3のX1とX2の値:1.6565; 0.36376
- Centroid 4のX1とX2の値:0.35134; 0.85358
K-Meansクラスタリングを実装できるいくつかのビジネスエリア
K-meansクラスタリングは用途の広いアルゴリズムであり、あらゆるタイプのグループ化の多くのビジネスユースケースに使用できます。 いくつかの例は次のとおりです。
Ø行動の分離:
- 購入履歴を使用した分割
- アプリケーション、Webサイト、またはプラットフォームアクティビティを使用した分割
- 顧客の興味に基づいて顧客のイメージを特定する
- モニタリング活動によるプロファイル作成
Ø画像スケーリング
- Pythonを使用した画像圧縮
Øセンサー測定:
- モーションセンサーのアクティビティタイプを検出する
- グループ画像
- オーディオを分割する
- スポットヘルスモニタリンググループ
Øボットまたは異常を特定します。
- アクティビティグループをボットから分離する
- 外れ値の検出をクリーンアップするための有効なアクティビティのグループを作成します
Ø在庫分類:

- 営業活動ごとに在庫グループを作成する
- 製造指標によって在庫グループを作成する
K-Meansクラスタリングの利点
トップの専門家がK-Meansクラスタリングアルゴリズムを好むのには理由があります。 それが提供するいくつかの利点:
- これは、高速で堅牢で、アルゴリズムを理解しやすいものです。
- 最終効率は比較的高い
- データセットが互いに異なる場合に驚異的な結果を提供します。 変数値が高い場合、K-Meansは比較的速く機能します
- K-Meansで生成されたクラスターは、他のクラスタリング手法よりも比較的タイトです。
必読: MATLABデータ型
結論
K-meansクラスタリングは、データクラスターを分析するために広く使用されているアプローチです。 コマンドを取得すると、結果をすばやく理解して適用し、提供することが容易になります。
この記事で願っています。 この分析手法を紹介することができます。 K-meansアルゴリズムに関する質問については、以下にコメントしてください。
さらに、この分野の研究に興味がある場合は、機械学習とAIプログラムのPGディプロマをご覧ください。このプログラムは、30以上のケーススタディと課題、業界の専門家による25以上のメンターシップセッション、10の実践的なハンズを提供する働く専門家向けに特別にキュレーションされています。 Capstoneプロジェクトでは、450時間以上の学習と配置の支援。
機械学習におけるKMeansクラスタリングとは何ですか?
これは、教師なし機械学習で使用される一般的なクラスタリングアルゴリズムです。 K Meansアルゴリズムは、Kセントロイドのランダムな識別の原理に基づいて機能します。 次のステップから、アルゴリズムはクラスター距離内で全体を最大化し、クラスター間距離全体を最小化しようとします。 K Meansアルゴリズムは、反復アプローチです。 各反復で、現在の重心のセットからK平均法を選択します。 次に、アルゴリズムは各観測値を最も近いK平均法に割り当てます。 2つのクラスター間の距離は、最も近い2つの観測値間の距離に基づいて計算されます。 クラスターの重心は、クラスター内のすべての観測値の平均として定義されます。
K Meansクラスタリングアルゴリズムの制限は何ですか?
K Meansにはいくつかの制限があり、使用するときに注意する必要があります。 K Meansは、外れ値に対してロバストではありません。 K Meansアルゴリズムは、すべてのデータポイントが重心からほぼ同じ距離にある場合にのみ適切に機能します。 一部のデータポイントが図心から遠く離れている場合、これにより、他のデータポイントのクラスターへの割り当てにバイアスがかかります。 K Meansは、独自のソリューションを保証するものではありません。 ポイントのクラスターが複数ある場合、アルゴリズムが実行されるたびにKMeansが同じ数のクラスターを返すという保証はありません。 K平均法はゆっくりと収束します。 小さなデータセットであっても、アルゴリズムの収束は非常に遅くなります。
K Meansクラスタリングの利点は何ですか?
単次元と多次元の両方に効果的です。 2次元と3次元の両方に適用できます。 これは、クラスターが多い状況で特に役立ちます。 クラスターは、データポイントの中間点で取得されます。 各クラスターの平均値が計算されます。 各点を標準偏差で割った後、平均値と比較します。 平均値と標準偏差は、すべてのクラスターとポイントについて計算されます。
