K 表示聚类 Matlab [附源码]
已发表: 2020-12-09K-means 聚类是数据专业人员最常用的技术之一。 由于算法的有效性,它在各种应用中受到众多行业的需求。
数据科学家的工作需要在多个阶段实施聚类。 目前许多大型项目都基于聚类算法,大大提高了对数据科学专业人士的需求。
其中一种算法是 K-means 聚类,这是本文的基本思想及其在 MATLAB 源代码中的实现。
在抓住主题之前,让我们快速了解一下集群是什么、它的意义以及如何在现实生活中实现它。 在这篇文章的最后,您将了解该算法对于理解大型数据集的重要性。
目录
什么是聚类?
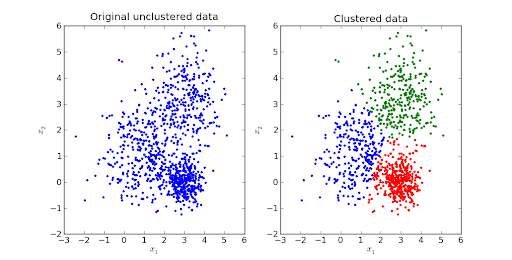
数据是任何应用程序最关键的组成部分,而集群只不过是相似数据点的组合。 顾名思义,聚类是根据数据模式将大量数据划分为子组或仅聚类的过程。
在机器学习中,当没有可用的预定义数据时应用聚类。 最终目的是将数据分组到具有高类内相似性的类中。

聚类用于探索数据。 可以使用它的一些现实示例是市场细分以找到具有相似行为的客户、图像分割/压缩、具有多个主题的文档聚类等。
这是处理数据以识别同质组以构建监督模型之前的必要步骤。 K-Means 聚类是一种无监督学习算法,因为我们必须寻找数据来整合相似的观察结果并形成不同的组。
我们来看看K-Means算法,它是应用最多、最简单的聚类算法之一。
K-Means 聚类
图片来源
K-means 聚类是最受欢迎的无监督机器学习算法之一。
无监督算法使用输入向量从数据集中得出结论,而不参考标记结果。
它是一种基于迭代距离或基于质心的算法,将数据集分成K个不同的子组(簇),其中每个数据点属于一个组。 增加了簇内数据点的相似度,使簇之间的距离保持最佳。
数据点与簇质心之间的距离保持在最小值,例如欧几里得距离。 在 K-Means 中,每个簇都链接到一个质心。 主要目的是最小化点与各自簇质心之间的距离。
K-Means 聚类如何工作?
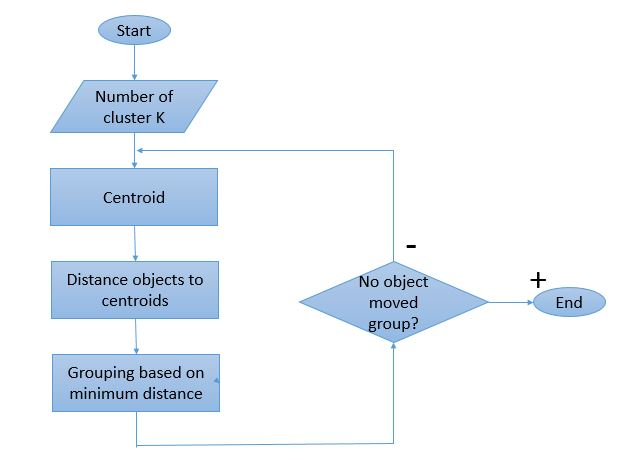
由于聚类过程意味着要执行多次迭代,因此 K-Means 算法具有独特的工作方式。 以下是其工作方式的分步说明:
图片来源
第 1 步:最初,定义集群的数量“ 第 2 步:将随机 K 个数据点初始化为每个集群的质心。
如果有 2 个簇,则“K”的值为 2。
第 3 步:执行多次迭代,直到分配给集群的数据点不变。
第 4 步:计算数据点与质心之间的平方距离之和。
步骤 5:将每个数据点分配到最近的集群(质心)以最小化距离。
第 6 步:取属于彼此的簇的质心的平均值。
这是一个单次迭代过程,用于计算质心并根据它们与质心的距离将点分配给集群。 一旦定义了所有质心,该过程就会停止。
描述 K-Means 聚类实现的示例
声明:作为著名的食品连锁店之一,麦当劳希望在加州开设连锁店,并希望找出能为他们带来最大收入的地点。
麦当劳已经有什么?
Ø 强大的电子商务存在
Ø 在线客户数据,用于分析频繁下单的地点
他们可能面临的挑战
- 分析频繁下单的区域。
- 了解该地区将开设多少家门店
- 找出所有区域内的网点位置,以保持商店和送货点之间的最小距离。
所有这些点都需要大量的分析和数学来研究。
这里如何使用 K-means 聚类方法?
使用预定义的 K 值,可以通过以下步骤实现 K-means 算法:
- 用 K 个对象划分为 K 个非空子集来识别商店位置。
- 确定分区的簇质心。
- 将每个位置分配给特定集群。
- 计算与每个位置的距离,并将点分配给与出口距离最小的集群。
- 经过一次迭代,重新分配点,找到形成的新簇的质心。
同样,K-Means 聚类算法可以应用于各种规模的各种应用。 酒店业、犯罪调查部门和图像大小调整等等。
K-Means 算法使用 R 、Python、MATLAB 等多种语言实现。在下一节中,我们将看看 K-Means Clustering MATLAB 是如何应用的。
阅读: Matlab 中的函数类型
使用 MATLAB 的 K-Means 算法
K-Means 是许多处理数据科学、机器学习、人工智能、密码学和网络安全的专业人士广泛使用的算法。

使用该算法的核心目标是找出每个簇的质心。 给程序员的数据是异构的。 这是绘制每个集群的质心并分配每个质心的坐标的 MATLAB 代码:
聚类 MATLAB
代码:
rng 默认; % 再现性
X = [randn(100,2)*0.75+ones(100,2);
randn(100,2)*0.5-ones(100,2)];
opts=statset('显示','final');
[idx,C]=kmeans(X,4,'Distance','cityblock','Replicates',5,'Options',opts);
plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12);
坚持,稍等;
plot(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12);
plot(X(idx==3,1),X(idx==3,2),'g.','MarkerSize',12);
plot(X(idx==4,1),X(idx==4,2),'y.','MarkerSize',12);
plot(C(:,1),C(:,2),'Kx','MarkerSize',15,'LineWidth',3);
legend('Cluster 1','Cluster 2','Cluster 3','Cluster 4','Centroids','Location','NW');
title('聚类分配和质心');
暂缓;
对于 i=1:size(C, 1)
display(['质心', num2str(i), ': X1 = ', num2str(C(i, 1)), '; X2 = ', num2str(C(i, 2))]);
结尾
输出:
显示四个聚类和各自质心的 MATLAB 窗口
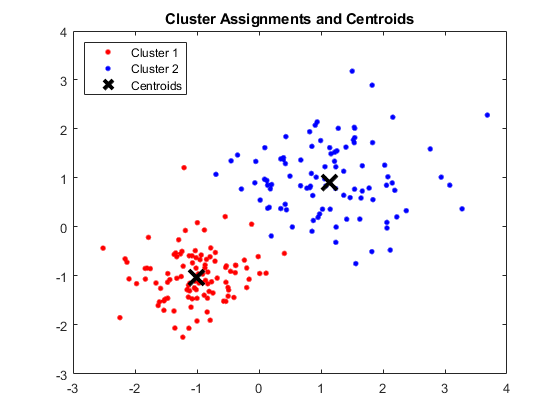
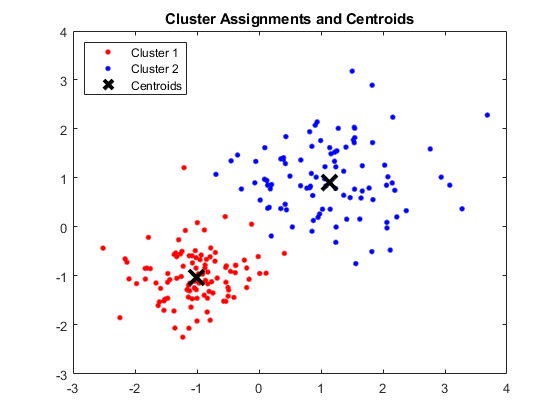
图片来源
结果:
得到的质心如下:
- 质心 1 的 X1 和 X2 的值:1.3661; 1.7232
- 质心 2 的 X1 和 X2 的值:-1.015; -1.053
- 质心 3 的 X1 和 X2 的值:1.6565; 0.36376
- 质心 4 的 X1 和 X2 的值:0.35134; 0.85358
可以实现 K-Means 聚类的一些业务领域
K-means 聚类是一种通用算法,可用于任何类型的分组的许多业务用例。 一些例子是:
Ø 行为隔离:
- 使用购买历史的划分
- 使用应用程序、网站或平台活动的部门
- 根据客户的兴趣识别客户的形象
- 使用监控活动创建配置文件
Ø 图像缩放
- 使用 Python 进行图像压缩
Ø 传感器测量:
- 检测运动传感器活动类型
- 组图像
- 分割音频
- 现场健康监测组
Ø 确定机器人或异常:
- 将活动组与机器人分开
- 做一组有效的活动来清理异常值检测
Ø 库存分类:

- 按销售活动制作库存组
- 按制造指标制作库存组
K-Means 聚类的优点
顶级专业人士偏爱 K-Means 聚类算法是有原因的。 它提供的一些好处:
- 它是一种快速、健壮且更易于理解的算法。
- 终端效率比较高
- 当数据集彼此不同时提供惊人的结果。 对于更高的变量值,K-Means 的工作速度相对更快
- 使用 K-Means 生成的聚类比其他聚类方法更紧密。
必读: MATLAB 数据类型
结论
K-means 聚类是一种广泛使用的数据聚类分析方法。 一旦你掌握了指挥权,就更容易理解、应用和快速交付结果。
我们希望这篇文章; 我们可以向您介绍这种分析技术。 有关 K-means 算法的任何疑问,请随时在下面发表评论。
此外,如果您对该研究领域感兴趣,请查看我们的机器学习和人工智能 PG 文凭课程,该课程专为在职专业人士提供 30 多个案例研究和作业、25 多个行业专家的指导课程、10 个实践手-在 Capstone 项目上,450 多个小时的学习和安置帮助。
什么是机器学习中的 K 均值聚类?
这是一种用于无监督机器学习的流行聚类算法。 K Means 算法的工作原理是随机识别 K 个质心。 从下一步开始,该算法尝试最大化总体内簇距离并最小化总体簇间距离。 K 均值算法是一种迭代方法。 在每次迭代中,它从当前的质心集中选择 K 均值。 然后,该算法将每个观测值分配给最接近的 K 均值。 两个聚类之间的距离是根据两个最接近的观测值之间的距离计算的。 簇的质心定义为簇中所有观测值的平均值。
K 均值聚类算法的局限性是什么?
K 均值有一些限制,您在使用它时需要牢记。 K 均值对异常值不稳健。 仅当所有数据点与质心的距离大致相同时,K 均值算法才有效。 如果您的一些数据点远离质心,这会使其他数据点分配给集群。 K 均值不保证唯一的解决方案。 如果您有多个点集群,则无法保证每次运行算法时 K 均值都会返回相同数量的集群。 K 均值收敛缓慢。 该算法收敛速度非常慢,即使在小数据集上也是如此。
K 均值聚类的优点是什么?
它对单维和多维都有效。 它适用于二维和三维。 它在有许多集群的情况下特别有用。 聚类是在数据点的中点获得的。 为每个集群计算平均值。 每个点除以标准偏差,然后与平均值进行比较。 计算所有簇和点的平均值和标准差。
