K หมายถึงการทำคลัสเตอร์ Matlab [ด้วยซอร์สโค้ด]
เผยแพร่แล้ว: 2020-12-09K-means clustering เป็นหนึ่งในเทคนิคที่ใช้กันมากที่สุดโดยผู้เชี่ยวชาญด้านข้อมูล เนื่องจากประสิทธิภาพของอัลกอริธึม เป็นที่ต้องการของอุตสาหกรรมจำนวนมากในการใช้งานที่หลากหลาย
งานของนักวิทยาศาสตร์ข้อมูลต้องมีการนำ Clustering ไปใช้ในหลายขั้นตอน โครงการขนาดใหญ่หลายแห่งในปัจจุบันใช้อัลกอริทึมการจัดกลุ่มและได้ยกระดับความต้องการผู้เชี่ยวชาญด้านวิทยาศาสตร์ข้อมูลอย่างมาก
หนึ่งในอัลกอริธึมเหล่านั้นคือการจัดกลุ่ม K-mean ซึ่งเป็นแนวคิดพื้นฐานของบทความนี้และการใช้งานกับซอร์สโค้ด MATLAB
ก่อนที่เราจะพูดถึงหัวข้อนี้ เรามาทำความรู้จักกับ Clustering กันก่อนว่า Clustering คืออะไร มีความสำคัญอย่างไร และจะนำไปปรับใช้ในชีวิตจริงได้อย่างไร ในตอนท้ายของโพสต์ คุณจะรู้ว่าอัลกอริทึมนี้มีความสำคัญเพียงใดในการทำความเข้าใจข้อมูลในชุดใหญ่
สารบัญ
การทำคลัสเตอร์คืออะไร?
ข้อมูลเป็นองค์ประกอบที่สำคัญที่สุดสำหรับแอปพลิเคชันใดๆ และคลัสเตอร์ไม่ได้เป็นเพียงการรวบรวมจุดข้อมูลที่คล้ายคลึงกันรวมกัน ตามชื่อที่กำหนดไว้อย่างชัดเจน การทำคลัสเตอร์คือกระบวนการแบ่งกลุ่มข้อมูลจำนวนมากออกเป็นกลุ่มย่อยหรือเฉพาะคลัสเตอร์ตามรูปแบบข้อมูล
ในการเรียนรู้ของเครื่อง การทำคลัสเตอร์จะถูกนำไปใช้เมื่อไม่มีข้อมูลที่กำหนดไว้ล่วงหน้า เป้าหมายสูงสุดคือการจัดกลุ่มข้อมูลออกเป็นคลาสที่มีความคล้ายคลึงกันภายในคลาสสูง

การทำคลัสเตอร์ใช้เพื่อสำรวจข้อมูล ตัวอย่างในชีวิตจริงบางส่วนที่สามารถนำมาใช้ได้ ได้แก่ การแบ่งส่วนตลาดเพื่อค้นหาลูกค้าที่มีพฤติกรรมคล้ายกัน การแบ่งส่วนภาพ/การบีบอัดภาพ การจัดกลุ่มเอกสารที่มีหลายหัวข้อ เป็นต้น
เป็นขั้นตอนที่จำเป็นก่อนประมวลผลข้อมูลเพื่อระบุกลุ่มที่เป็นเนื้อเดียวกันสำหรับการสร้างแบบจำลองภายใต้การดูแล การจัดกลุ่ม K-Means เป็นอัลกอริธึมการเรียนรู้ที่ไม่มีผู้ดูแล เนื่องจากเราต้องค้นหาข้อมูลเพื่อรวมการ สังเกตที่คล้ายคลึงกันและสร้างกลุ่มที่แตกต่างกัน
มาดู อัลกอริธึม K-Means ซึ่งเป็นหนึ่งในอัลกอริธึมการจัดกลุ่มที่ง่ายที่สุดและนำไปใช้มากที่สุด
K-หมายถึงการจัดกลุ่ม
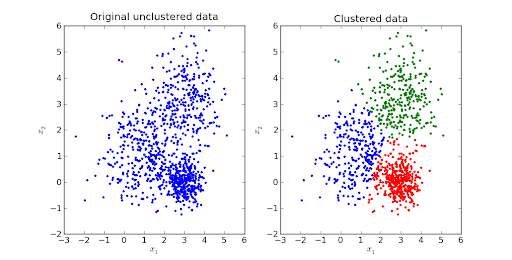
ที่มาของภาพ
การจัดกลุ่ม K-means เป็นหนึ่งในอัลกอริธึมการเรียนรู้ของเครื่องที่ไม่มีผู้ดูแลที่ต้องการมากที่สุด
อัลกอริธึมที่ไม่ได้รับการดูแลจะทำการสรุปจากชุดข้อมูลโดยใช้เวกเตอร์อินพุตโดยไม่อ้างอิงถึงผลลัพธ์ที่ติดฉลาก
เป็นอัลกอริธึมตามระยะทางแบบวนซ้ำหรือแบบเซนทรอยด์ที่แยกชุดข้อมูลออกเป็น กลุ่มย่อยที่แตกต่างกันของ K (คลัสเตอร์) โดยที่จุดข้อมูลแต่ละจุดอยู่ใน กลุ่ม เดียว ความคล้ายคลึงกันของจุดข้อมูลภายในคลัสเตอร์จะเพิ่มขึ้น และระยะห่างระหว่างคลัสเตอร์จะถูกรักษาให้เหมาะสมที่สุด
ระยะห่างระหว่างจุดข้อมูลและเซนทรอยด์ของกระจุกดาวจะถูกเก็บไว้ให้น้อยที่สุด เช่น ระยะห่างแบบยุคลิด ใน K-Means แต่ละคลัสเตอร์จะเชื่อมโยงกับเซนทรอยด์ จุดมุ่งหมายหลักคือเพื่อลดระยะห่างระหว่างจุดและศูนย์กลางของคลัสเตอร์ตามลำดับ
K-Means Clustering ทำงานอย่างไร
เนื่องจากกระบวนการจัดกลุ่มหมายถึงต้องทำซ้ำหลายครั้ง อัลกอริธึม K-Means จึงมีวิธีการทำงานที่ไม่เหมือนใคร นี่คือคำอธิบายทีละขั้นตอนเกี่ยวกับวิธีการทำงาน:
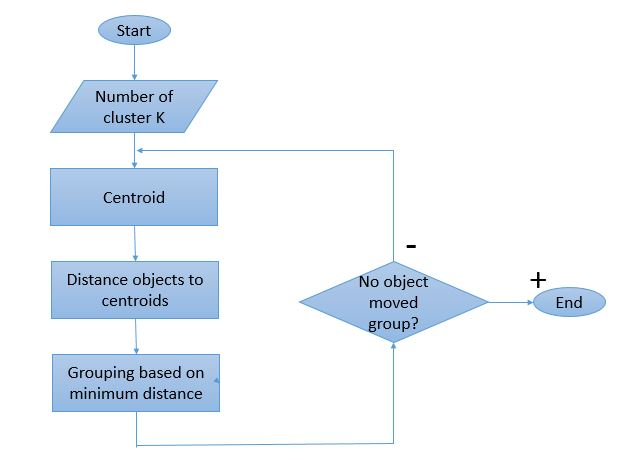
ที่มาของภาพ
ขั้นตอนที่ 1: เริ่มแรก กำหนดจำนวนคลัสเตอร์ ' ขั้นตอนที่ 2: เริ่มต้นจุดข้อมูล K แบบสุ่มเป็นเซนทรอยด์สำหรับแต่ละคลัสเตอร์
หากมี 2 คลัสเตอร์ ค่าของ 'K' จะเป็น 2
ขั้นตอนที่ 3: ทำซ้ำหลาย ๆ ครั้งจนกว่าจุดข้อมูลที่กำหนดไปยังคลัสเตอร์จะไม่เปลี่ยนแปลง
ขั้นตอนที่ 4: คำนวณผลรวมของระยะห่างกำลังสองระหว่างจุดข้อมูลกับเซนทรอยด์
ขั้นตอนที่ 5: จัดสรรจุดข้อมูลแต่ละจุดไปยังคลัสเตอร์ที่ใกล้ที่สุด (เซนทรอยด์) เพื่อลดระยะห่าง
ขั้นตอนที่ 6: หาค่าเฉลี่ยของเซนทรอยด์ของกลุ่มที่เป็นของกันและกัน
นี่เป็นกระบวนการวนซ้ำครั้งเดียวสำหรับการคำนวณเซนทรอยด์และกำหนดจุดให้กับคลัสเตอร์ตามระยะห่างจากเซนทรอยด์ เมื่อกำหนดเซนทรอยด์ทั้งหมดแล้ว กระบวนการจะหยุดลง
ตัวอย่างภาพประกอบที่แสดงให้เห็นการนำ K-Means Clustering ไปปฏิบัติ
คำชี้แจง: หนึ่งในเครือข่ายอาหารที่มีชื่อเสียง McDonald's ต้องการเปิดสาขาทั่วแคลิฟอร์เนียและต้องการหาสถานที่ตั้งที่จะดึงรายได้สูงสุดให้พวกเขา
สิ่งที่ McDonald's มีอยู่แล้ว?
Ø สถานะอีคอมเมิร์ซที่แข็งแกร่ง
Ø ข้อมูลลูกค้าออนไลน์สำหรับวิเคราะห์สถานที่ที่มีการสั่งซื้อบ่อย
ความท้าทายที่อาจเกิดขึ้นได้
- การวิเคราะห์พื้นที่ที่มีการสั่งซื้อบ่อยครั้ง
- ทำความเข้าใจจำนวนสาขาที่จะเปิดในพื้นที่
- หาที่ตั้งของร้านค้าภายในพื้นที่ทั้งหมด เพื่อรักษาระยะห่างขั้นต่ำระหว่างร้านค้ากับจุดจัดส่ง
ประเด็นทั้งหมดเหล่านี้ต้องการการวิเคราะห์และคณิตศาสตร์อย่างมากในการทำงาน
K-means Clustering Method สามารถใช้ที่นี่ได้อย่างไร
ด้วยค่าที่กำหนดไว้ล่วงหน้าของ K อัลกอริทึม K-means สามารถนำไปใช้ในขั้นตอนต่อไปนี้:
- การระบุตำแหน่งร้านค้าด้วย K Partition ของอ็อบเจ็กต์เป็น K เซ็ตย่อยที่ไม่ว่างเปล่า
- การกำหนดคลัสเตอร์ centroids ของพาร์ติชัน
- การกำหนดสถานที่แต่ละแห่งให้กับคลัสเตอร์เฉพาะ
- การคำนวณระยะทางจากแต่ละสถานที่และจัดสรรคะแนนไปยังคลัสเตอร์ที่ระยะห่างน้อยที่สุดกับทางออก
- หลังจากการวนซ้ำหนึ่งครั้ง การจัดสรรคะแนนใหม่ ค้นหาจุดศูนย์กลางของคลัสเตอร์ใหม่ที่เกิดขึ้น
ในทำนองเดียวกัน อัลกอริธึมการจัดกลุ่ม K-Means สามารถนำไปใช้กับแอปพลิเคชันต่างๆ ในระดับต่างๆ ได้ อุตสาหกรรมการบริการ แผนกสืบสวนอาชญากรรม และการปรับขนาดรูปภาพ เป็นต้น

อัลกอริธึม K-Means ถูกใช้งานโดยใช้ภาษาต่างๆ เช่น R , Python, MATLAB เป็นต้น ในหัวข้อถัดไป เราจะมาดูกันว่า K-Means Clustering MATLAB ถูกนำไปใช้อย่างไร
อ่าน: ประเภทของฟังก์ชันใน Matlab
อัลกอริทึม K-Means โดยใช้ MATLAB
K-Means เป็นอัลกอริธึมที่ใช้กันมากซึ่งใช้โดยผู้เชี่ยวชาญหลายคนที่เกี่ยวข้องกับวิทยาศาสตร์ข้อมูล การเรียนรู้ของเครื่อง ปัญญาประดิษฐ์ การเข้ารหัส และความปลอดภัยทางไซเบอร์
วัตถุประสงค์หลักของการใช้อัลกอริธึมนี้คือการหาเซนทรอยด์ของแต่ละคลัสเตอร์ ข้อมูลที่ให้กับโปรแกรมเมอร์มีความแตกต่างกัน นี่คือรหัส MATLAB สำหรับการพล็อตเซนทรอยด์ของแต่ละคลัสเตอร์และกำหนดพิกัดของแต่ละเซนทรอยด์:
การทำคลัสเตอร์ MATLAB
รหัส:
rng ค่าเริ่มต้น; % สำหรับการทำซ้ำ
X = [แรนด์(100,2)*0.75+อัน(100,2);
randn(100,2)*0.5-ones(100,2)];
opts=statset('แสดงผล','สุดท้าย');
[idx,C]=kmeans(X,4,'Distance','cityblock','Replicates',5,'Options',opts);
พล็อต(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12);
เดี๋ยว;
พล็อต(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12);
พล็อต(X(idx==3,1),X(idx==3,2),'g.','MarkerSize',12);
พล็อต(X(idx==4,1),X(idx==4,2),'y.','MarkerSize',12);
พล็อต (C(:,1),C(:,2),'Kx','MarkerSize',15,'LineWidth',3);
ตำนาน ('คลัสเตอร์ 1', 'คลัสเตอร์ 2', 'คลัสเตอร์ 3', 'คลัสเตอร์ 4', 'เซนทรอยด์', 'ตำแหน่ง', 'NW');
title('การกำหนดคลัสเตอร์และเซนทรอยด์');
ออกจาก;
สำหรับผม=1:ขนาด(C, 1)
display(['Centroid', num2str(i), ': X1 = ', num2str(C(i, 1)), '; X2 = ', num2str(C(i, 2))]);
จบ
เอาท์พุท:
หน้าต่าง MATLAB แสดงสี่คลัสเตอร์และเซ็นทรอยด์ที่เกี่ยวข้อง
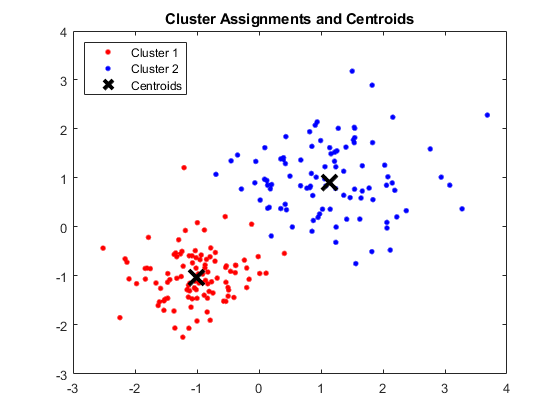
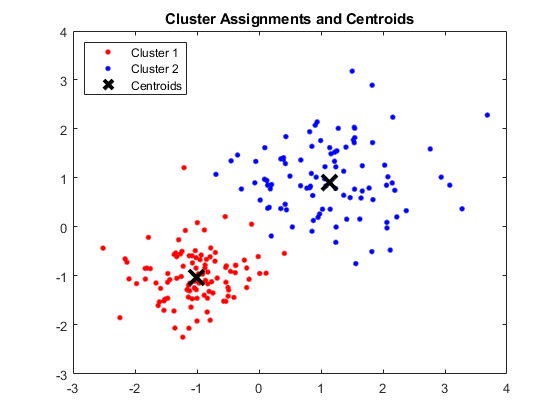
ที่มาของภาพ
ผล:
เซนทรอยด์ที่ได้รับมีดังนี้:
- ค่าของ X1 & X2 สำหรับ Centroid 1: 1.3661; 1.7232
- ค่าของ X1 & X2 สำหรับ Centroid 2: -1.015; -1.053
- ค่าของ X1 & X2 สำหรับ Centroid 3: 1.6565; 0.36376
- ค่าของ X1 & X2 สำหรับ Centroid 4: 0.35134; 0.85358
บางพื้นที่ธุรกิจที่สามารถดำเนินการคลัสเตอร์ K-Means ได้
การจัดกลุ่ม K-means เป็นอัลกอริธึมที่ใช้งานได้หลากหลายและสามารถใช้ได้กับกรณีการใช้งานทางธุรกิจจำนวนมากสำหรับการจัดกลุ่มประเภทใดก็ได้ ตัวอย่างบางส่วน ได้แก่ :
Ø การแยกพฤติกรรม:
- กองโดยใช้ประวัติการซื้อ
- การแบ่งส่วนการใช้งานแอพพลิเคชั่น เว็บไซต์ หรือกิจกรรมแพลตฟอร์ม
- ระบุภาพลักษณ์ของลูกค้าตามความสนใจ
- การสร้างโปรไฟล์ด้วยกิจกรรมการตรวจสอบ
Ø การปรับขนาดภาพ
- การบีบอัดภาพโดยใช้ Python
Ø การวัดเซนเซอร์:
- ตรวจจับประเภทกิจกรรมของเซ็นเซอร์ตรวจจับความเคลื่อนไหว
- ภาพหมู่
- แบ่งเสียง
- กลุ่มตรวจสุขภาพเฉพาะจุด
Ø ตรวจสอบบอทหรือความผิดปกติ:
- แยกกลุ่มกิจกรรมออกจากบอท
- สร้างกลุ่มของกิจกรรมที่ถูกต้องเพื่อล้างการตรวจจับค่าผิดปกติ
Ø การจำแนกประเภทสินค้าคงคลัง:

- สร้างกลุ่มสินค้าคงคลังตามกิจกรรมการขาย
- สร้างกลุ่มสินค้าคงคลังตามเมตริกการผลิต
ข้อดีของการจัดกลุ่ม K-Means
มีเหตุผลว่าทำไมผู้เชี่ยวชาญชั้นนำถึงเลือกใช้อัลกอริทึมการจัดกลุ่ม K-Means ประโยชน์บางประการที่มีให้:
- เป็นอัลกอริทึมที่รวดเร็ว แข็งแกร่ง และเข้าใจง่าย
- ประสิทธิภาพสุดท้ายค่อนข้างสูง
- ให้ผลลัพธ์ที่ยอดเยี่ยมเมื่อชุดข้อมูลต่างกัน สำหรับค่าตัวแปรที่สูงกว่า K-Means จะทำงานค่อนข้างเร็วกว่า
- คลัสเตอร์ที่ผลิตด้วย K-Means นั้นค่อนข้างเข้มงวดกว่าวิธีการจัดกลุ่มแบบอื่นๆ
ต้องอ่าน: MATLAB ประเภทข้อมูล
บทสรุป
K-means clustering เป็นแนวทางที่ใช้กันอย่างแพร่หลายสำหรับการวิเคราะห์กลุ่มข้อมูล เมื่อคุณได้รับคำสั่งแล้ว จะง่ายต่อการเข้าใจและนำไปใช้และส่งผลอย่างรวดเร็ว
เราหวังว่าจะมีบทความนี้ เราสามารถแนะนำให้คุณรู้จักกับเทคนิคการวิเคราะห์นี้ สำหรับข้อสงสัยใด ๆ เกี่ยวกับอัลกอริทึม K-means โปรดแสดงความคิดเห็นด้านล่าง
นอกจากนี้ หากสาขาวิชานี้สนใจ คุณลองดู หลักสูตร PG Diploma in Machine Learning และ AI ซึ่งได้รับการดูแลจัดการเป็นพิเศษสำหรับมืออาชีพด้านการทำงาน โดยเสนอกรณีศึกษาและการมอบหมายงานมากกว่า 30 รายการ เซสชันการให้คำปรึกษามากกว่า 25 รายการจากผู้เชี่ยวชาญในอุตสาหกรรม 10 มือเชิงปฏิบัติ ในโครงการ Capstone ความช่วยเหลือด้านการเรียนรู้และการจัดตำแหน่งมากกว่า 450 ชั่วโมง
K หมายถึงการจัดกลุ่มในการเรียนรู้ของเครื่องคืออะไร?
นี่เป็นอัลกอริธึมการจัดกลุ่มที่เป็นที่นิยมซึ่งใช้ในการเรียนรู้ของเครื่องโดยไม่ได้รับการดูแล K หมายถึงอัลกอริธึมทำงานบนหลักการของการระบุ K centroids แบบสุ่ม จากขั้นตอนถัดไป อัลกอริธึมพยายามเพิ่มระยะโดยรวมภายในคลัสเตอร์ให้สูงสุด และลดระยะโดยรวมระหว่างคลัสเตอร์ให้เหลือน้อยที่สุด K หมายถึงอัลกอริทึมเป็นวิธีการวนซ้ำ ในการวนซ้ำแต่ละครั้ง จะเลือกค่า K จากชุดเซนทรอยด์ชุดปัจจุบัน จากนั้นอัลกอริธึมจะกำหนดให้การสังเกตแต่ละครั้งมีค่า K ที่ใกล้เคียงที่สุด ระยะห่างระหว่างสองคลัสเตอร์คำนวณตามระยะห่างระหว่างการสังเกตที่ใกล้ที่สุดทั้งสอง Centroid ของคลัสเตอร์ถูกกำหนดให้เป็นค่าเฉลี่ยของการสังเกตทั้งหมดในคลัสเตอร์
อัลกอริทึมการจัดกลุ่ม K หมายถึงมีข้อจำกัดอย่างไร
มีข้อ จำกัด บางประการของ K หมายถึงที่คุณต้องการทราบเมื่อใช้งาน K หมายถึงไม่แข็งแกร่งสำหรับค่าผิดปกติ อัลกอริธึม K หมายถึงทำงานได้ดีเมื่อจุดข้อมูลทั้งหมดของคุณอยู่ห่างจากเซนทรอยด์เท่ากัน หากจุดข้อมูลบางจุดของคุณอยู่ไกลจากเซนทรอยด์ จะเป็นการเบี่ยงเบนการกำหนดจุดข้อมูลอื่นๆ ให้กับคลัสเตอร์ K หมายถึงไม่รับประกันโซลูชันที่ไม่เหมือนใคร หากคุณมีจุดคลัสเตอร์มากกว่าหนึ่งคลัสเตอร์ ไม่มีการรับประกันว่า K หมายถึงจะส่งคืนจำนวนคลัสเตอร์เท่ากันทุกครั้งที่รันอัลกอริทึม K หมายถึงมาบรรจบกันอย่างช้าๆ อัลกอริทึมมาบรรจบกันช้ามาก แม้กระทั่งในชุดข้อมูลขนาดเล็ก
ข้อดีของการจัดกลุ่ม K หมายถึงคืออะไร?
มีประสิทธิภาพทั้งมิติเดียวและหลายมิติ สามารถใช้ได้ทั้งในสองและสามมิติ มีประโยชน์อย่างยิ่งในสถานการณ์ที่มีคลัสเตอร์จำนวนมาก คลัสเตอร์ได้มาจากจุดกึ่งกลางของจุดข้อมูล ค่าเฉลี่ยจะถูกคำนวณสำหรับแต่ละคลัสเตอร์ แต่ละจุดหารด้วยค่าเบี่ยงเบนมาตรฐาน แล้วนำไปเปรียบเทียบกับค่าเฉลี่ย ค่าเฉลี่ยและค่าเบี่ยงเบนมาตรฐานจะคำนวณสำหรับคลัสเตอร์และจุดทั้งหมด
