K significa agrupamiento Matlab [con código fuente]

La agrupación en clústeres de K-means es una de las técnicas más utilizadas por los profesionales de datos. Debido a la eficacia del algoritmo, numerosas industrias lo demandan en diversas aplicaciones.

El trabajo de un científico de datos requiere la implementación de Clustering en muchas etapas. Muchos proyectos a gran escala se basan actualmente en el algoritmo de agrupación y han elevado drásticamente el nivel de demanda de los profesionales de la ciencia de datos.

Uno de esos algoritmos es el agrupamiento de K-means, que es la idea básica de este artículo y su implementación con el código fuente de MATLAB.

Antes de entender el tema, echemos un vistazo rápido a lo que es la agrupación en clústeres, su importancia y cómo se puede implementar en la vida real. Al final de la publicación, sabrá cuán crucial es este algoritmo para comprender los datos en conjuntos grandes.

¿Qué es la agrupación?

Los datos son el componente más crítico para cualquier aplicación, y un clúster no es más que una acumulación de puntos de datos similares combinados. Como su nombre lo define claramente, la agrupación en clústeres es el proceso de dividir una gran parte de los datos en subgrupos o solo en clústeres según el patrón de datos.

En el aprendizaje automático, la agrupación en clústeres se aplica cuando no hay datos predefinidos disponibles. El objetivo final es agrupar los datos en clases con alta similitud intraclase.

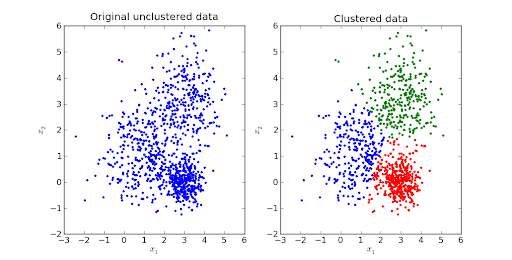
La agrupación se utiliza para explorar datos. Algunos ejemplos de la vida real en los que se puede utilizar son la segmentación del mercado para encontrar clientes con comportamientos similares, la segmentación/compresión de imágenes, la agrupación de documentos con múltiples temas, etc.

Es un paso necesario antes de procesar datos para identificar grupos homogéneos para construir modelos supervisados. La agrupación en clústeres de K-Means es un algoritmo de aprendizaje no supervisado, ya que tenemos que buscar datos para integrar observaciones similares y formar grupos distintos.

Echemos un vistazo al algoritmo K-Means , que es uno de los algoritmos de agrupamiento más simples y más aplicados.

Agrupación de K-Means

Fuente de imagen

La agrupación en clústeres de K-means es uno de los algoritmos de aprendizaje automático no supervisados ​​más deseados.

Los algoritmos no supervisados ​​extraen conclusiones a partir de conjuntos de datos utilizando vectores de entrada sin referirse a los resultados etiquetados.

Es un algoritmo iterativo basado en la distancia o en el centroide que segrega el conjunto de datos en K subgrupos distintos (clusters) donde cada punto de datos pertenece a un grupo . Se aumenta la similitud de los puntos de datos dentro del grupo y la distancia entre los grupos se mantiene óptima.

La distancia entre los puntos de datos y el centroide del clúster se mantiene al mínimo, como la distancia euclidiana. En K-Means, cada grupo está vinculado a un centroide. El objetivo principal es minimizar las distancias entre los puntos y el centroide del clúster respectivo.

¿Cómo funciona el agrupamiento de K-Means?

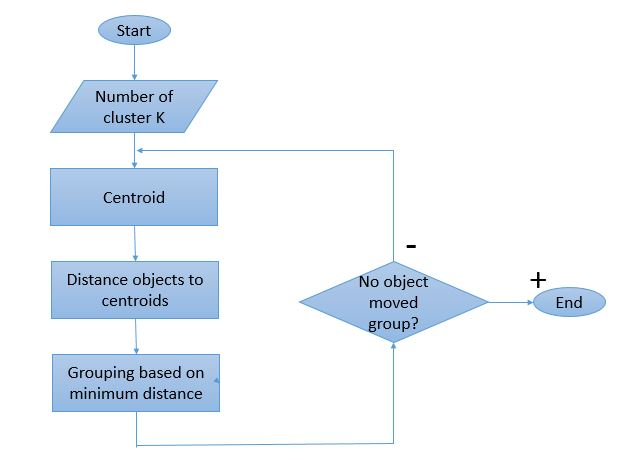
Como el proceso de agrupación implica que se deben realizar varias iteraciones, el algoritmo K-Means tiene una forma única de trabajar. Aquí hay una explicación paso a paso de la forma en que funciona:

Fuente de imagen

Paso 1: Inicialmente, defina el número de clústeres ' Paso 2: inicialice K puntos de datos aleatorios como centroides para cada grupo.

Si hay 2 clústeres, el valor de 'K' será 2.

Paso 3: realice varias iteraciones hasta que los puntos de datos asignados a los clústeres no cambien.

Paso 4: Calcule la suma de la distancia al cuadrado entre los puntos de datos y los centroides.

Paso 5: asigne cada punto de datos al grupo más cercano (centroide) para minimizar la distancia.

Paso 6: Tome un promedio de los centroides de los conglomerados que se pertenecen entre sí.

Este es un proceso de iteración única realizado para calcular el centroide y asignar los puntos al grupo en función de su distancia desde el centroide. Una vez definidos todos los centroides, se detiene el proceso.

Un ejemplo ilustrativo que representa la implementación de la agrupación en clústeres de K-Means

Propuesta: McDonald's, una de las famosas cadenas de comida, quiere abrir una cadena de puntos de venta en todo California y quiere averiguar los lugares que les reportarán los máximos ingresos.

¿Qué McDonald's ya tiene?

Ø Una fuerte presencia de comercio electrónico

Ø Datos de clientes en línea para analizar ubicaciones desde donde se realizan pedidos con frecuencia

Posibles desafíos que podrían enfrentar

• Analizar las zonas desde donde se realizan los pedidos con frecuencia.
• Comprender cuántos puntos de venta se abrirán en el área
• Determine las ubicaciones de los puntos de venta dentro de todas las áreas para mantener una distancia mínima entre la tienda y los puntos de entrega.

Todos estos puntos necesitan mucho análisis y matemáticas para trabajar.

¿Cómo se puede usar aquí el método de agrupación en clústeres de K-medias?

Con un valor predefinido de K, el algoritmo de K-medias se puede implementar en los siguientes pasos:

• Identificar las ubicaciones de las tiendas con K Partición de objetos en K subconjuntos no vacíos.
• Determinación de los centroides de conglomerados de la partición.
• Asignación de cada ubicación a un clúster específico.
• Calcular las distancias desde cada ubicación y asignar puntos al clúster donde la distancia es mínima con la salida.
• Después de una iteración, reasignando los puntos, encuentre el centroide del nuevo grupo formado.

Asimismo, el algoritmo de agrupamiento de K-Means se puede aplicar a una variedad de aplicaciones en escalas variadas. La industria hotelera, los departamentos de investigación de delitos y el cambio de tamaño de imágenes, por nombrar algunos.

El algoritmo K-Means se implementa utilizando muchos lenguajes como R , Python, MATLAB, etc. En la siguiente sección, veremos cómo se aplica MATLAB K-Means Clustering.

Leer: Tipos de funciones en Matlab

Algoritmo de K-Means utilizando MATLAB

K-Means es un algoritmo ampliamente utilizado por muchos profesionales que se ocupan de la ciencia de datos, el aprendizaje automático, la inteligencia artificial, la criptografía y la ciberseguridad.

El objetivo central de usar este algoritmo es encontrar el centroide de cada grupo. Los datos que se le dan a un programador son heterogéneos. Aquí está el código de MATLAB para trazar el centroide de cada grupo y asignar las coordenadas de cada centroide:

agrupamientoMATLAB

Código:

rng por defecto; % de reproducibilidad

X = [randn(100,2)*0.75+unos(100,2);

randn(100,2)*0.5-unos(100,2)];

opts=statset('Pantalla','final');

[idx,C]=kmeans(X,4,'Distancia','manzana','Replicas',5,'Opciones',opts);

plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12);

esperar;

plot(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12);

plot(X(idx==3,1),X(idx==3,2),'g.','MarkerSize',12);

plot(X(idx==4,1),X(idx==4,2),'y.','MarkerSize',12);

plot(C(:,1),C(:,2),'Kx','MarkerSize',15,'LineWidth',3);

legend('Cluster 1','Cluster 2','Cluster 3','Cluster 4','Centroids', 'Location','NW');

title('Asignaciones de clúster y centroides');

esperar;

para i=1:tamaño(C, 1)

display(['Centroid ', num2str(i), ': X1 = ', num2str(C(i, 1)), '; X2 = ', num2str(C(i, 2))]);

final

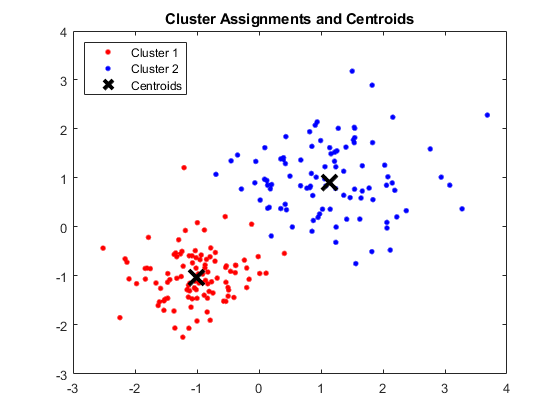
Producción:

Ventana de MATLAB que muestra cuatro clústeres y sus respectivos centroides

Fuente de imagen

Resultados:

Los centroides obtenidos son los siguientes:

1. El valor de X1 y X2 para Centroid 1: 1.3661; 1.7232
2. El valor de X1 y X2 para Centroid 2: -1.015; -1.053
3. El valor de X1 y X2 para Centroid 3: 1.6565; 0.36376
4. El valor de X1 y X2 para Centroid 4: 0.35134; 0.85358

Algunas áreas comerciales donde se puede implementar la agrupación en clústeres de K-Means

La agrupación en clústeres de K-means es un algoritmo versátil y se puede utilizar para muchos casos de uso comercial para cualquier tipo de agrupación. Algunos ejemplos son:

Ø Segregación conductual:

• División usando el historial de compras
• División que utiliza actividades de aplicaciones, sitios web o plataformas
• Identificar la imagen de los clientes en función de sus intereses.
• Creación de perfiles con actividades de seguimiento

Ø Escalado de imagen

• Compresión de imágenes usando Python

ØMedidas del sensor:

• Detectar tipos de actividad de sensores de movimiento
• Agrupar imágenes
• Dividir audio
• Detectar grupos de monitoreo de salud

Ø Determinar bots o anomalías:

• Separe los grupos de actividades de los bots
• Cree un grupo de actividades válidas para limpiar la detección de valores atípicos

Ø Clasificación del inventario:

• Hacer grupos de inventario por actividad de ventas
• Hacer grupos de inventario por métricas de fabricación

Ventajas de la agrupación en clústeres de K-Means

Hay una razón por la que los mejores profesionales prefieren el algoritmo de agrupación en clústeres K-Means. Algunos beneficios que ofrece:

• Es un algoritmo rápido, robusto y fácil de entender.
• La eficiencia final es relativamente alta.
• Ofrece resultados fenomenales cuando los conjuntos de datos son diferentes entre sí. Para valores de variables más altos, K-Means funciona comparativamente más rápido
• Los conglomerados producidos con K-Means son relativamente más ajustados que otros métodos de conglomerado.

Debe leer: Tipos de datos de MATLAB

Conclusión

El agrupamiento de K-medias es un enfoque ampliamente utilizado para analizar grupos de datos. Una vez que obtiene el comando, es más fácil de entender y aplicar y entregar resultados rápidamente.

Esperamos con este artículo; Podríamos presentarte esta técnica de análisis. Para cualquier consulta sobre el algoritmo K-means, no dude en comentar a continuación.

Además, si este campo de estudio le interesa, eche un vistazo a nuestro programa PG Diploma in Machine Learning and AI , que está especialmente diseñado para profesionales que trabajan y ofrece más de 30 estudios de casos y asignaciones, más de 25 sesiones de tutoría de expertos de la industria, 10 Manos prácticas- en Capstone Projects, más de 450 horas de aprendizaje y asistencia de colocación.

¿Qué es la agrupación en clústeres de K Means en el aprendizaje automático?

Este es un algoritmo de agrupamiento popular utilizado en el aprendizaje automático no supervisado. El algoritmo K Means funciona según el principio de identificación de K centroides al azar. A partir del siguiente paso, el algoritmo intenta maximizar la distancia total dentro de los grupos y también minimizar la distancia total entre grupos. El algoritmo K Means es un enfoque iterativo. En cada iteración, selecciona las K Medias del conjunto actual de centroides. Luego, el algoritmo asigna cada observación a la media K más cercana. La distancia entre dos conglomerados se calcula en función de la distancia entre las dos observaciones más cercanas. El centroide de un conglomerado se define como el promedio de todas las observaciones en el conglomerado.

¿Cuáles son las limitaciones del algoritmo de agrupamiento de K Means?

Hay algunas limitaciones de K Means que querrá tener en cuenta al usarlo. K Means no es resistente a los valores atípicos. El algoritmo K Means solo funciona bien cuando todos los puntos de datos están aproximadamente a la misma distancia del centroide. Si algunos de sus puntos de datos están lejos del centroide, esto sesgará la asignación de otros puntos de datos a los clústeres. K Means no garantiza una solución única. Si tiene más de un grupo de puntos, no hay garantía de que K Means devuelva la misma cantidad de grupos cada vez que se ejecuta el algoritmo. K Significa que converge lentamente. El algoritmo converge muy lentamente, incluso en pequeños conjuntos de datos.

¿Cuáles son las ventajas de la agrupación en clústeres de K Means?

Es efectivo tanto para dimensiones simples como múltiples. Es aplicable tanto en dos como en tres dimensiones. Es particularmente útil en situaciones donde hay muchos clústeres. Los grupos se obtienen en el punto medio de los puntos de datos. Se calcula un valor medio para cada grupo. Cada punto se divide por la desviación estándar y luego se compara con el valor medio. El valor medio y la desviación estándar se calculan para todos los grupos y puntos.