K bedeutet Clustering von Matlab [mit Quellcode]
Veröffentlicht: 2020-12-09K-Means-Clustering ist eine der am häufigsten verwendeten Techniken von Datenexperten. Aufgrund der Leistungsfähigkeit des Algorithmus wird er von zahlreichen Branchen in unterschiedlichen Anwendungen gefordert.
Die Arbeit eines Datenwissenschaftlers erfordert die Implementierung von Clustering in vielen Phasen. Viele Großprojekte basieren derzeit auf dem Clustering-Algorithmus und haben die Messlatte für die Nachfrage von Data-Science-Experten drastisch erhöht.
Einer dieser Algorithmen ist das K-Means-Clustering, das die Grundidee dieses Artikels und seiner Implementierung mit dem MATLAB-Quellcode darstellt.
Bevor wir das Thema in den Griff bekommen, werfen wir einen kurzen Blick darauf, was Clustering ist, was es bedeutet und wie es in der Praxis umgesetzt werden kann. Am Ende des Beitrags werden Sie erfahren, wie wichtig dieser Algorithmus für das Verständnis von Daten in großen Mengen ist.
Inhaltsverzeichnis
Was ist Clustering?
Daten sind die kritischste Komponente für jede Anwendung, und ein Cluster ist nichts anderes als eine Ansammlung ähnlicher Datenpunkte kombiniert. Wie der Name klar definiert, ist Clustering der Prozess, bei dem ein großer Datenblock basierend auf dem Datenmuster in Untergruppen oder nur Cluster aufgeteilt wird.
Beim maschinellen Lernen wird Clustering angewendet, wenn keine vordefinierten Daten verfügbar sind. Das ultimative Ziel ist es, Daten in Klassen mit hoher Ähnlichkeit innerhalb der Klasse zu gruppieren.

Clustering wird verwendet, um Daten zu untersuchen. Einige Beispiele aus der Praxis, wo es verwendet werden kann, sind Marktsegmentierung, um Kunden mit ähnlichen Verhaltensweisen zu finden, Bildsegmentierung/-komprimierung, Dokumenten-Clustering mit mehreren Themen usw.
Es ist ein erforderlicher Schritt vor der Verarbeitung von Daten, um homogene Gruppen zum Erstellen von überwachten Modellen zu identifizieren. K-Means-Clustering ist ein unüberwachter Lernalgorithmus, da wir nach Daten suchen müssen, um ähnliche Beobachtungen zu integrieren und unterschiedliche Gruppen zu bilden.
Werfen wir einen Blick auf den K-Means- Algorithmus, der einer der am häufigsten angewandten und einfachsten Clustering-Algorithmen ist.
K-Means-Clustering
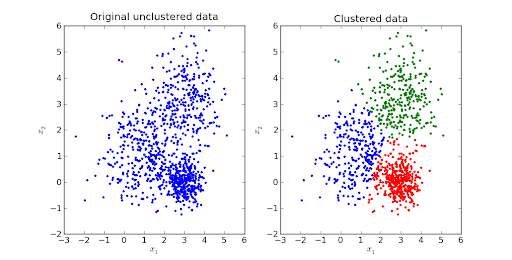
Bildquelle
K-Means-Clustering ist einer der begehrtesten Algorithmen für unbeaufsichtigtes maschinelles Lernen.
Unüberwachte Algorithmen ziehen Schlussfolgerungen aus Datensätzen unter Verwendung von Eingabevektoren, ohne sich auf gekennzeichnete Ergebnisse zu beziehen.
Es ist ein iterativer entfernungsbasierter oder zentroidbasierter Algorithmus, der den Datensatz in K verschiedene Untergruppen (Cluster) aufteilt, wobei jeder Datenpunkt zu einer Gruppe gehört . Die Ähnlichkeit der Intra-Cluster-Datenpunkte wird erhöht und der Abstand zwischen den Clustern wird optimal gehalten.
Der Abstand zwischen den Datenpunkten und dem Schwerpunkt des Clusters wird auf einem Minimum gehalten, wie etwa dem euklidischen Abstand. In K-Means ist jeder Cluster mit einem Schwerpunkt verknüpft. Primäres Ziel ist es, die Abstände zwischen den Punkten und dem jeweiligen Clusterschwerpunkt zu minimieren.
Wie funktioniert K-Means-Clustering?
Da der Clustering-Prozess mehrere Iterationen erfordert, hat der K-Means-Algorithmus eine einzigartige Arbeitsweise. Hier ist eine Schritt-für-Schritt-Erklärung, wie es funktioniert:
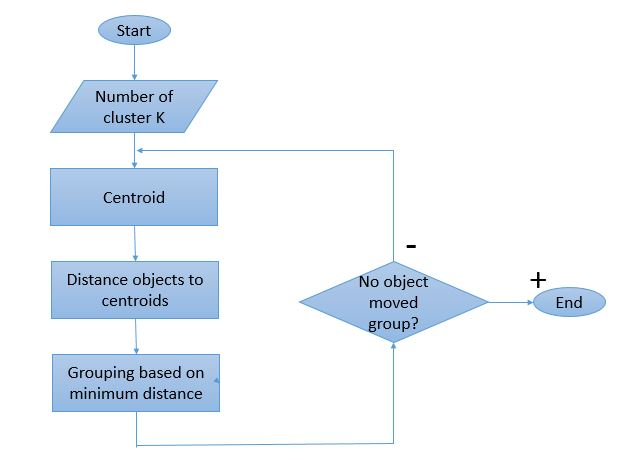
Bildquelle
Schritt 1: Definieren Sie zunächst die Anzahl der Cluster ' Schritt 2: Initialisieren Sie zufällige K Datenpunkte als Schwerpunkte für jeden Cluster.
Wenn es 2 Cluster gibt, ist der Wert von 'K' 2.
Schritt 3: Führen Sie mehrere Iterationen durch, bis sich die den Clustern zugewiesenen Datenpunkte nicht ändern.
Schritt 4: Berechnen Sie die Summe des quadrierten Abstands zwischen Datenpunkten und den Schwerpunkten.
Schritt 5: Ordnen Sie jeden Datenpunkt dem nächstgelegenen Cluster (Schwerpunkt) zu, um die Entfernung zu minimieren.
Schritt 6: Durchschnitt der Schwerpunkte der zueinander gehörenden Cluster bilden.
Dies ist ein einzelner Iterationsprozess, der zum Berechnen des Schwerpunkts und zum Zuweisen der Punkte zu dem Cluster basierend auf ihrem Abstand vom Schwerpunkt durchgeführt wird. Sobald alle Schwerpunkte definiert sind, wird der Prozess gestoppt.
Ein illustratives Beispiel, das die Implementierung von K-Means-Clustering darstellt
Aussage: McDonald's, eine der berühmten Lebensmittelketten, möchte eine Filialkette in ganz Kalifornien eröffnen und die Standorte herausfinden, die ihnen den maximalen Umsatz bringen.
Was hat McDonald's schon?
Ø Eine starke E-Commerce-Präsenz
Ø Online-Kundendaten zur Analyse von Standorten, von denen die Bestellungen häufig getätigt werden
Mögliche Herausforderungen, denen sie sich stellen könnten
- Analysieren der Bereiche, aus denen die Bestellungen häufig getätigt werden.
- Verstehen Sie, wie viele Filialen in der Umgebung eröffnet werden sollen
- Finden Sie die Standorte für die Verkaufsstellen in allen Bereichen heraus, um einen Mindestabstand zwischen dem Geschäft und den Lieferpunkten einzuhalten.
All diese Punkte erfordern viel Analyse und Mathematik, um daran zu arbeiten.
Wie kann hier die K-Means-Clustering-Methode eingesetzt werden?
Mit einem vordefinierten Wert von K kann der K-Means-Algorithmus in den folgenden Schritten implementiert werden:
- Identifizieren der Speicherorte mit K Partitionierung von Objekten in K nicht leere Teilmengen.
- Bestimmen der Clusterschwerpunkte der Partition.
- Jeden Standort einem bestimmten Cluster zuweisen.
- Berechnen der Entfernungen von jedem Standort und Zuordnen von Punkten zu dem Cluster, wo die Entfernung zum Outlet minimal ist.
- Finden Sie nach einer Iteration, indem Sie die Punkte neu zuweisen, den Schwerpunkt des neu gebildeten Clusters.
Ebenso kann der K-Means-Clustering-Algorithmus auf eine Vielzahl von Anwendungen in unterschiedlichen Maßstäben angewendet werden. Das Gastgewerbe, die Kriminalpolizei und die Größenänderung von Bildern, um nur einige zu nennen.

Der K-Means-Algorithmus wird mit vielen Sprachen wie R , Python, MATLAB usw. implementiert. Im nächsten Abschnitt werden wir uns ansehen, wie K-Means Clustering MATLAB angewendet wird.
Lesen Sie: Funktionstypen in Matlab
K-Means-Algorithmus mit MATLAB
K-Means ist ein weit verbreiteter Algorithmus, der von vielen Fachleuten verwendet wird, die sich mit Datenwissenschaft, maschinellem Lernen, künstlicher Intelligenz, Kryptografie und Cybersicherheit befassen.
Das Hauptziel der Verwendung dieses Algorithmus besteht darin, den Schwerpunkt jedes Clusters herauszufinden. Die Daten, die einem Programmierer gegeben werden, sind heterogen. Hier ist der MATLAB-Code zum Zeichnen des Schwerpunkts jedes Clusters und zum Zuweisen der Koordinaten jedes Schwerpunkts:
Clustering von MATLAB
Code:
rng-Standard; % Zur Reproduzierbarkeit
X = [Randn(100,2)*0,75+Einsen(100,2);
randn(100,2)*0,5-Einsen(100,2)];
opts=statset('Anzeige','final');
[idx,C]=kmeans(X,4,'Distance','cityblock','Replicates',5,'Options',opts);
plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12);
festhalten;
plot(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12);
plot(X(idx==3,1),X(idx==3,2),'g.','MarkerSize',12);
plot(X(idx==4,1),X(idx==4,2),'y.','MarkerSize',12);
plot(C(:,1),C(:,2),'Kx','MarkerSize',15,'LineWidth',3);
legend('Cluster 1','Cluster 2','Cluster 3','Cluster 4','Centroids', 'Location','NW');
title('Clusterzuweisungen und Zentroide');
abwarten;
für i=1:Größe(C, 1)
display(['Schwerpunkt', num2str(i), ': X1 = ', num2str(C(i, 1)), '; X2 = ', num2str(C(i, 2))]);
Ende
Ausgabe:
MATLAB-Fenster mit vier Clustern und entsprechenden Zentroiden
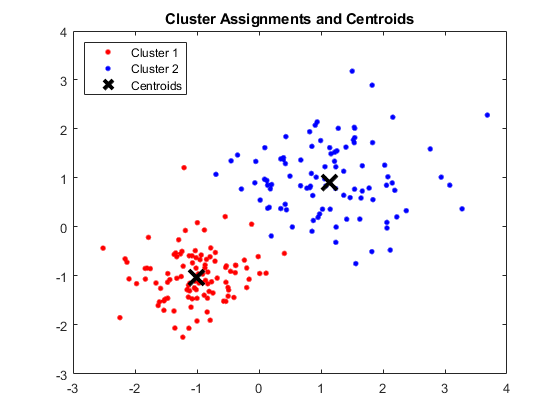
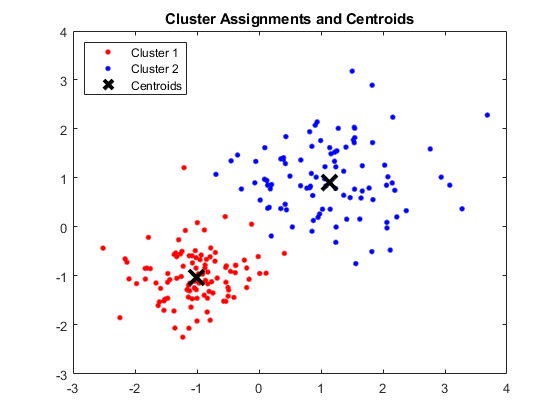
Bildquelle
Ergebnisse:
Die erhaltenen Schwerpunkte sind wie folgt:
- Der Wert von X1 & X2 für Centroid 1: 1,3661; 1,7232
- Der Wert von X1 & X2 für Centroid 2: -1.015; -1.053
- Der Wert von X1 & X2 für Centroid 3: 1,6565; 0,36376
- Der Wert von X1 & X2 für Centroid 4: 0,35134; 0,85358
Einige Geschäftsbereiche, in denen K-Means-Clustering implementiert werden kann
K-Means-Clustering ist ein vielseitiger Algorithmus und kann für viele geschäftliche Anwendungsfälle für jede Art von Gruppierung verwendet werden. Einige Beispiele sind:
Ø Verhaltenstrennung:
- Aufteilung anhand der Kaufhistorie
- Aufteilung unter Verwendung von Anwendungs-, Website- oder Plattformaktivitäten
- Identifizieren Sie das Image der Kunden anhand ihrer Interessen
- Profilerstellung mit Überwachungsaktivitäten
Ø Bildskalierung
- Bildkomprimierung mit Python
Ø Sensormessungen:
- Aktivitätstypen von Bewegungssensoren erkennen
- Gruppenbilder
- Audio teilen
- Erkennen Sie Gesundheitsüberwachungsgruppen
Ø Bots oder Anomalien ermitteln:
- Trennen Sie Aktivitätsgruppen von Bots
- Erstellen Sie eine Gruppe gültiger Aktivitäten, um die Ausreißererkennung zu bereinigen
Ø Inventarklassifizierung:

- Erstellen Sie Inventargruppen nach Verkaufsaktivitäten
- Inventargruppen nach Fertigungskennzahlen erstellen
Vorteile von K-Means-Clustering
Es gibt einen Grund, warum Top-Profis den K-Means-Clustering-Algorithmus bevorzugen. Einige Vorteile, die es bietet:
- Es ist ein schneller, robuster und einfacher zu verstehender Algorithmus.
- Der Endwirkungsgrad ist relativ hoch
- Bietet phänomenale Ergebnisse, wenn sich Datensätze voneinander unterscheiden. Bei höheren Variablenwerten arbeitet K-Means vergleichsweise schneller
- Die mit K-Means erzeugten Cluster sind relativ enger als andere Clustering-Methoden.
Muss gelesen werden: MATLAB-Datentypen
Fazit
K-Means-Clustering ist ein weit verbreiteter Ansatz zur Analyse von Datenclustern. Sobald Sie das Kommando erlangt haben, ist es einfacher zu verstehen und anzuwenden und schnell Ergebnisse zu liefern.
Wir hoffen mit diesem Artikel; wir könnten Ihnen diese Analysetechnik vorstellen. Bei Fragen zum K-Means-Algorithmus können Sie unten einen Kommentar hinterlassen.
Wenn Sie sich für dieses Studienfach interessieren, werfen Sie außerdem einen Blick auf unser PG Diploma in Machine Learning and AI - Programm, das speziell für Berufstätige kuratiert wurde und mehr als 30 Fallstudien und Aufgaben, mehr als 25 Mentoring-Sitzungen von Branchenexperten und 10 praktische Übungen bietet. bei Capstone Projects, mehr als 450 Stunden Lern- und Vermittlungsunterstützung.
Was ist K Means-Clustering beim maschinellen Lernen?
Dies ist ein beliebter Clustering-Algorithmus, der beim unüberwachten maschinellen Lernen verwendet wird. Der K-Means-Algorithmus arbeitet nach dem Prinzip der zufälligen Identifizierung von K-Zentroiden. Ab dem nächsten Schritt versucht der Algorithmus, den Gesamtabstand innerhalb der Cluster zu maximieren und auch den Gesamtabstand zwischen den Clustern zu minimieren. Der K-Means-Algorithmus ist ein iterativer Ansatz. In jeder Iteration wählt es die K-Means aus dem aktuellen Satz von Zentroiden aus. Der Algorithmus ordnet dann jede Beobachtung dem nächsten K-Mittelwert zu. Die Entfernung zwischen zwei Clustern wird basierend auf der Entfernung zwischen den beiden nächsten Beobachtungen berechnet. Der Schwerpunkt eines Clusters ist definiert als der Durchschnitt aller Beobachtungen im Cluster.
Was sind die Einschränkungen des K-Means-Clustering-Algorithmus?
Es gibt einige Einschränkungen von K Means, die Sie bei der Verwendung beachten sollten. K Means ist nicht robust gegenüber Ausreißern. Der K-Means-Algorithmus funktioniert nur dann gut, wenn alle Ihre Datenpunkte ungefähr den gleichen Abstand vom Schwerpunkt haben. Wenn einige Ihrer Datenpunkte weit vom Schwerpunkt entfernt sind, wird dies die Zuordnung anderer Datenpunkte zu Clustern beeinflussen. K Means garantiert keine einzigartige Lösung. Wenn Sie mehr als ein Cluster von Punkten haben, gibt es keine Garantie dafür, dass K Means bei jeder Ausführung des Algorithmus dieselbe Anzahl von Clustern zurückgibt. K Mittelwerte konvergieren langsam. Der Algorithmus konvergiert selbst bei kleinen Datensätzen sehr langsam.
Was sind die Vorteile von K-Means-Clustering?
Es ist sowohl für Einzel- als auch für Mehrfachdimensionen wirksam. Es ist sowohl in zwei als auch in drei Dimensionen anwendbar. Dies ist besonders nützlich in Situationen, in denen viele Cluster vorhanden sind. Die Cluster werden am Mittelpunkt der Datenpunkte erhalten. Für jeden Cluster wird ein Mittelwert berechnet. Jeder Punkt wird durch die Standardabweichung dividiert und dann mit dem Mittelwert verglichen. Für alle Cluster und Punkte werden der Mittelwert und die Standardabweichung berechnet.
