K significa clustering Matlab [com código fonte]

O clustering K-means é uma das técnicas mais usadas por profissionais de dados. Devido à eficácia do algoritmo, é exigido por inúmeras indústrias em diversas aplicações.

O trabalho de um cientista de dados requer a implementação do Clustering em vários estágios. Atualmente, muitos projetos de grande escala são baseados no algoritmo de clustering e aumentaram drasticamente o nível de exigência dos profissionais de ciência de dados.

Um desses algoritmos é o clustering K-means, que é a ideia básica deste artigo e sua implementação com o código fonte do MATLAB.

Antes de encerrar o tópico, vamos dar uma olhada rápida no que é Clustering, seu significado e como ele pode ser implementado na vida real. Ao final do post, você saberá como esse algoritmo é crucial para entender dados em grandes conjuntos.

O que é Clusterização?

Os dados são o componente mais crítico para qualquer aplicativo, e um cluster nada mais é do que um acúmulo de pontos de dados semelhantes combinados. Como o nome define claramente, Clustering é o processo de dividir uma grande quantidade de dados em subgrupos ou apenas clusters com base no padrão de dados.

No aprendizado de máquina, o clustering é aplicado quando não há dados predefinidos disponíveis. O objetivo final é agrupar dados em classes com alta similaridade intraclasse.

O clustering é usado para explorar dados. Alguns exemplos da vida real onde pode ser usado são na segmentação de mercado para encontrar clientes com comportamentos semelhantes, segmentação/compressão de imagens, agrupamento de documentos com vários tópicos, etc.

É uma etapa necessária antes do processamento de dados para identificar grupos homogêneos para a construção de modelos supervisionados. O agrupamento K-Means é um algoritmo de aprendizado não supervisionado, pois precisamos procurar dados para integrar observações semelhantes e formar grupos distintos.

Vamos dar uma olhada no algoritmo K-Means , que é um dos algoritmos de agrupamento mais aplicados e mais simples.

Agrupamento K-Means

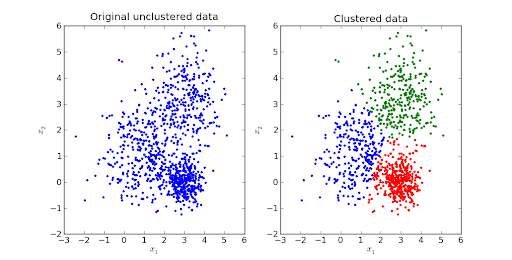
Fonte da imagem

O clustering K-means é um dos algoritmos de aprendizado de máquina não supervisionados mais desejados.

Algoritmos não supervisionados tiram conclusões de conjuntos de dados usando vetores de entrada sem se referir a resultados rotulados.

É um algoritmo iterativo baseado em distância ou centroide que segrega o conjunto de dados em K subgrupos distintos (clusters) onde cada ponto de dados pertence a um grupo . A similaridade dos pontos de dados intra-cluster é aumentada e a distância entre os clusters é mantida ótima.

A distância entre os pontos de dados e o centroide do cluster é mantida no mínimo, como a distância euclidiana. No K-Means, cada cluster está vinculado a um centroide. O objetivo principal é minimizar as distâncias entre os pontos e o respectivo centroide do cluster.

Como funciona o cluster K-Means?

Como o processo de agrupamento implica em várias iterações a serem realizadas, o algoritmo K-Means tem uma forma única de trabalhar. Aqui está uma explicação passo a passo de como funciona:

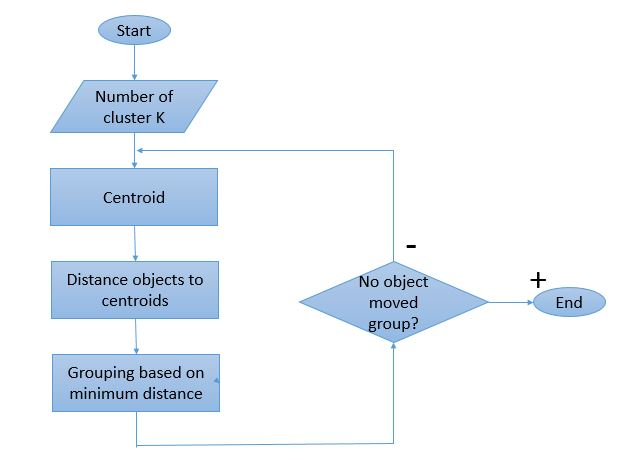
Fonte da imagem

Passo 1: Inicialmente, defina o número de clusters ' Etapa 2: Inicialize K pontos de dados aleatórios como centroides para cada cluster.

Se houver 2 clusters, o valor de 'K' será 2.

Etapa 3: execute várias iterações até que os pontos de dados atribuídos aos clusters não sejam alterados.

Passo 4: Calcule a soma da distância ao quadrado entre os pontos de dados e os centróides.

Etapa 5: Aloque cada ponto de dados para o cluster mais próximo (centroide) para minimizar a distância.

Passo 6: Faça uma média dos centróides dos clusters pertencentes um ao outro.

Este é um processo de iteração único realizado para calcular o centroide e atribuir os pontos ao cluster com base em sua distância do centroide. Uma vez que todos os centróides são definidos, o processo é interrompido.

Um exemplo ilustrativo que descreve a implementação do agrupamento K-Means

Declaração: Uma das famosas cadeias de alimentos, o McDonald's quer abrir uma cadeia de pontos de venda em toda a Califórnia e quer descobrir os locais que lhes trarão receita máxima.

O que o McDonald's já tem?

Ø Uma forte presença de e-commerce

Ø Dados de clientes online para análise de locais de onde os pedidos são feitos com frequência

Possíveis desafios que eles podem enfrentar

• Analisando as áreas de onde os pedidos são feitos com frequência.
• Compreender quantos pontos de venda devem ser abertos na área
• Descubra os locais dos pontos de venda em todas as áreas para manter uma distância mínima entre a loja e os pontos de entrega.

Todos esses pontos precisam de muita análise e matemática para trabalhar.

Como o método de agrupamento K-means pode ser usado aqui?

Com um valor predefinido de K, o algoritmo K-means pode ser implementado nas seguintes etapas:

• Identificando os locais de armazenamento com K Partição de objetos em K subconjuntos não vazios.
• Determinando os centróides do cluster da partição.
• Atribuindo cada local a um cluster específico.
• Calculando as distâncias de cada local e alocando pontos para o cluster onde a distância é mínima com a saída.
• Após uma iteração, redistribuindo os pontos, encontre o centróide do novo cluster formado.

Da mesma forma, o algoritmo K-Means Clustering pode ser aplicado a uma variedade de aplicações em escalas variadas. A indústria de hospitalidade, departamentos de investigação de crimes e redimensionamento de imagens, para citar alguns.

O algoritmo K-Means é implementado usando muitas linguagens como R , Python, MATLAB, etc. Na próxima seção, veremos como o K-Means Clustering MATLAB é aplicado.

Leia: Tipos de funções no Matlab

Algoritmo K-Means usando MATLAB

O K-Means é um algoritmo amplamente usado por muitos profissionais que lidam com ciência de dados, aprendizado de máquina, inteligência artificial, criptografia e segurança cibernética.

O objetivo central de usar este algoritmo é descobrir o centroide de cada cluster. Os dados fornecidos a um programador são heterogêneos. Aqui está o código MATLAB para traçar o centroide de cada cluster e atribuir as coordenadas de cada centroide:

Agrupando MATLAB

Código:

rng padrão; % Para reprodutibilidade

X = [randn(100,2)*0,75+unidades(100,2);

randn(100,2)*0,5-ones(100,2)];

opts=statset('Exibir','final');

[idx,C]=kmeans(X,4,'Distance','cityblock','Replicates',5,'Options',opts);

plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12);

aguentar;

plot(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12);

plot(X(idx==3,1),X(idx==3,2),'g.','MarkerSize',12);

plot(X(idx==4,1),X(idx==4,2),'y.','MarkerSize',12);

plot(C(:,1),C(:,2),'Kx','MarkerSize',15,'LineWidth',3);

legend('Cluster 1','Cluster 2','Cluster 3','Cluster 4','Centroids', 'Location','NW');

title('Atribuições de cluster e centroides');

adiar;

para i=1:tamanho(C, 1)

display(['Centroid ', num2str(i), ': X1 = ', num2str(C(i, 1)), '; X2 = ', num2str(C(i, 2))]);

fim

Saída:

Janela MATLAB mostrando quatro clusters e respectivos centróides

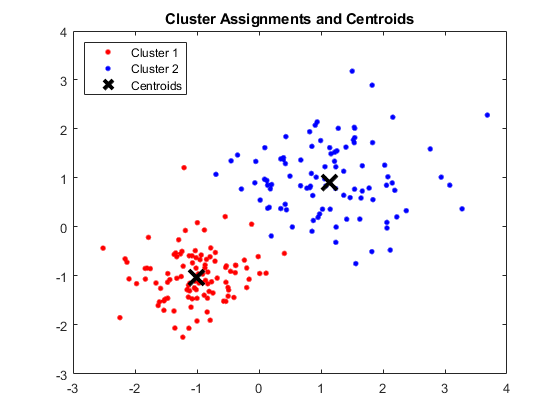
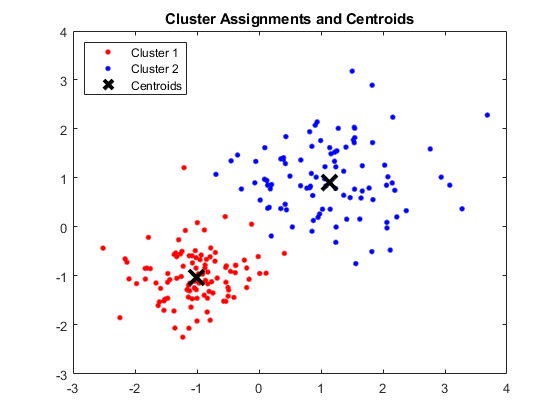
Fonte da imagem

Resultados:

Os centróides obtidos são os seguintes:

1. O valor de X1 & X2 para Centroid 1: 1,3661; 1,7232
2. O valor de X1 e X2 para Centroid 2: -1,015; -1,053
3. O valor de X1 & X2 para Centroid 3: 1,6565; 0,36376
4. O valor de X1 & X2 para Centroid 4: 0,35134; 0,85358

Algumas áreas de negócios onde o cluster K-Means pode ser implementado

O agrupamento K-means é um algoritmo versátil e pode ser usado para muitos casos de uso de negócios para qualquer tipo de agrupamento. Alguns exemplos são:

Ø Segregação Comportamental:

• Divisão usando histórico de compras
• Divisão usando atividades de aplicativos, sites ou plataformas
• Identifique a imagem dos clientes com base em seus interesses
• Criação de perfil com atividades de monitoramento

Ø Dimensionamento de Imagem

• Compressão de imagem usando Python

Ø Medições do sensor:

• Detectar tipos de atividade de sensores de movimento
• Imagens do grupo
• Dividir áudio
• Grupos de monitoramento de integridade do Spot

Ø Determinar bots ou anomalias:

• Separe os grupos de atividades dos bots
• Faça um grupo de atividades válidas para limpar a detecção de valores discrepantes

Ø Classificação do inventário:

• Faça grupos de estoque por atividade de vendas
• Faça grupos de inventário por métricas de fabricação

Vantagens do cluster K-Means

Há uma razão pela qual os melhores profissionais preferem o algoritmo de agrupamento K-Means. Alguns benefícios que ela oferece:

• É um algoritmo rápido, robusto e fácil de entender.
• A eficiência final é relativamente alta
• Oferece resultados fenomenais quando os conjuntos de dados são diferentes uns dos outros. Para valores de variáveis ​​mais altos, K-Means funciona comparativamente mais rápido
• Os clusters produzidos com K-Means são relativamente mais rígidos do que outros métodos de clustering.

Deve ler: Tipos de dados MATLAB

Conclusão

O clustering K-means é uma abordagem amplamente utilizada para analisar clusters de dados. Uma vez que você ganha o comando, é mais fácil entender e aplicar e entregar resultados rapidamente.

Esperamos com este artigo; poderíamos apresentá-lo a esta técnica de análise. Para qualquer dúvida sobre o algoritmo K-means, sinta-se à vontade para comentar abaixo.

Além disso, se este campo de estudo lhe interessar, dê uma olhada em nosso programa PG Diploma in Machine Learning and AI , que é especialmente selecionado para profissionais que oferecem mais de 30 estudos de caso e tarefas, mais de 25 sessões de orientação de especialistas do setor, 10 Hands-hands-práticos. em Capstone Projects, mais de 450 horas de aprendizagem e assistência de colocação.

O que é o clustering K Means no aprendizado de máquina?

Este é um algoritmo de agrupamento popular usado em aprendizado de máquina não supervisionado. O algoritmo K Means trabalha com o princípio de identificação de K centroides aleatoriamente. A partir da próxima etapa, o algoritmo tenta maximizar a distância geral dentro do cluster e também minimizar a distância geral entre os clusters. O algoritmo K Means é uma abordagem iterativa. Em cada iteração, ele seleciona o K Means do conjunto atual de centróides. O algoritmo então atribui cada observação à média K mais próxima. A distância entre dois clusters é calculada com base na distância entre as duas observações mais próximas. O Centroid de um cluster é definido como a média de todas as observações no cluster.

Quais são as limitações do algoritmo de agrupamento K Means?

Existem algumas limitações do K Means que você deve ter em mente ao usá-lo. K Means não é robusto a valores discrepantes. O algoritmo K Means só funciona bem quando todos os seus pontos de dados estão aproximadamente à mesma distância do centroide. Se alguns de seus pontos de dados estiverem longe do centroide, isso influenciará a atribuição de outros pontos de dados aos clusters. K Means não garante uma solução única. Se você tiver mais de um cluster de pontos, não há garantia de que K Means retornará o mesmo número de clusters toda vez que o algoritmo for executado. K Média converge lentamente. O algoritmo converge muito lentamente, mesmo em pequenos conjuntos de dados.

Quais são as vantagens do agrupamento K Means?

É eficaz para dimensões simples e múltiplas. É aplicável em duas e três dimensões. É particularmente útil em situações em que há muitos clusters. Os clusters são obtidos no ponto médio dos pontos de dados. Um valor médio é calculado para cada cluster. Cada ponto é dividido pelo desvio padrão e depois comparado com o valor médio. O valor médio e o desvio padrão são calculados para todos os clusters e pontos.