K înseamnă Clustering Matlab [Cu cod sursă]

Gruparea K-means este una dintre cele mai frecvent utilizate tehnici de către profesioniștii în date. Datorită eficacității algoritmului, acesta este solicitat de numeroase industrii în diverse aplicații.

Munca unui cercetător de date necesită implementarea Clusteringului în mai multe etape. Multe proiecte la scară largă se bazează în prezent pe algoritmul de clustering și au ridicat drastic ștacheta pentru cererea profesioniștilor din știința datelor.

Unul dintre acești algoritmi este gruparea K-means, care este ideea de bază a acestui articol și implementarea sa cu codul sursă MATLAB.

Înainte de a pune în aplicare subiectul, să aruncăm o privire rapidă la ce este Clustering-ul, semnificația sa și cum poate fi implementat în viața reală. Până la sfârșitul postării, vei ajunge să știi cât de crucial este acest algoritm pentru înțelegerea datelor în seturi mari.

Ce este Clustering?

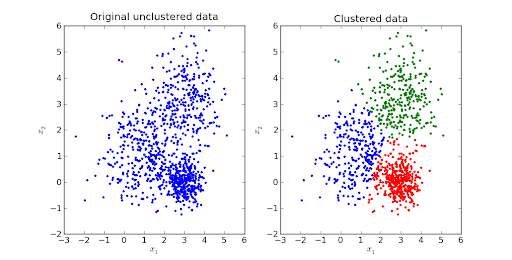
Datele sunt componenta cea mai critică pentru orice aplicație, iar un cluster nu este altceva decât o acumulare de puncte de date similare combinate. După cum definește în mod clar și numele, Clustering este procesul de împărțire a unei mari părți de date în subgrupuri sau numai clustere pe baza modelului de date.

În învățarea automată, clusterizarea este aplicată atunci când nu există date predefinite disponibile. Scopul final este de a grupa datele în clase cu similaritate ridicată în cadrul clasei.

Clusteringul este folosit pentru a explora datele. Câteva exemple din viața reală în care poate fi utilizat sunt în segmentarea pieței pentru a găsi clienți cu comportamente similare, segmentarea/comprimarea imaginilor, gruparea documentelor cu mai multe subiecte etc.

Este un pas necesar înainte de prelucrarea datelor pentru a identifica grupuri omogene pentru construirea modelelor supravegheate. Gruparea K-Means este un algoritm de învățare nesupravegheat, deoarece trebuie să căutăm date pentru a integra observații similare și a forma grupuri distincte.

Să aruncăm o privire la algoritmul K-Means , care este unul dintre cei mai aplicați și cei mai simpli algoritmi de grupare.

K-Means Clustering

Sursa imaginii

Gruparea K-means este unul dintre cei mai doriti algoritmi de învățare automată nesupravegheată.

Algoritmii nesupravegheați fac concluzii din seturi de date folosind vectori de intrare fără a se referi la rezultatele etichetate.

Este un algoritm iterativ bazat pe distanță sau bazat pe centroid care segrega setul de date în K subgrupuri distincte (clustere) în care fiecare punct de date aparține unui grup . Asemănarea punctelor de date intra-cluster este crescută, iar distanța dintre clustere este menținută optimă.

Distanța dintre punctele de date și centroidul clusterului este menținută la minim, cum ar fi distanța euclidiană. În K-Means, fiecare cluster este legat de un centroid. Scopul principal este de a minimiza distanțele dintre puncte și centroidul clusterului respectiv.

Cum funcționează K-Means Clustering?

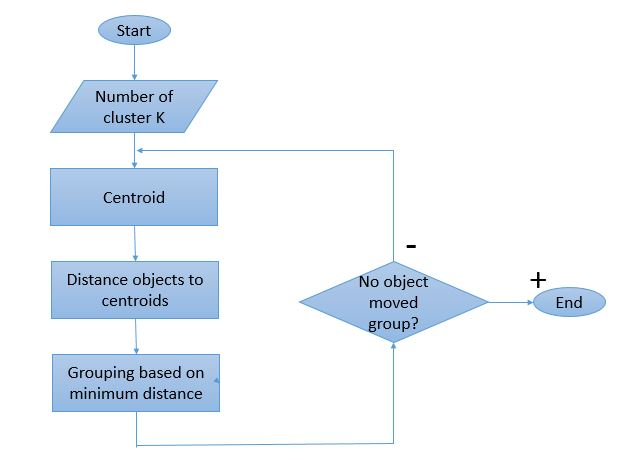
Deoarece procesul de grupare înseamnă mai multe iterații care trebuie efectuate, algoritmul K-Means are un mod unic de lucru. Iată o explicație pas cu pas a modului în care funcționează:

Sursa imaginii

Pasul 1: Inițial, definiți numărul de clustere „ Pasul 2: Inițializați K puncte de date aleatoare ca centroizi pentru fiecare cluster.

Dacă există 2 grupuri, valoarea lui „K” va fi 2.

Pasul 3: Efectuați mai multe iterații până când punctele de date alocate clusterelor nu se modifică.

Pasul 4: Calculați suma distanței pătrate dintre punctele de date și centroizi.

Pasul 5: Alocați fiecare punct de date celui mai apropiat cluster (centroid) pentru a minimiza distanța.

Pasul 6: Luați o medie a centroizilor clusterelor aparținând unul altuia.

Acesta este un singur proces de iterație efectuat pentru calcularea centroidului și atribuirea punctelor clusterului pe baza distanței lor față de centroid. Odată ce toți centroizii sunt definiți, procesul este oprit.

Un exemplu ilustrativ care descrie implementarea grupării K-Means

Declarație: Unul dintre renumitele lanțuri alimentare, McDonald's vrea să deschidă un lanț de magazine în California și vrea să afle locațiile care le vor aduce venituri maxime.

Ce are deja McDonald's?

Ø O prezență puternică în comerțul electronic

Ø Datele online ale clientilor pentru analizarea locatiilor de unde se fac frecvent comenzile

Posibile provocări cu care s-ar putea confrunta

• Analizând zonele de unde se fac frecvent comenzile.
• Înțelegeți câte puncte de desfacere vor fi deschise în zonă
• Descoperiți locațiile punctelor de vânzare din toate zonele pentru a păstra o distanță minimă între magazin și punctele de livrare.

Toate aceste puncte necesită multă analiză și matematică pentru a lucra.

Cum poate fi folosită aici metoda K-means Clustering?

Cu o valoare predefinită de K, algoritmul K-means poate fi implementat în următorii pași:

• Identificarea locațiilor magazinului cu K Partițiunea obiectelor în K subseturi nevide.
• Determinarea centroizilor clusterului partiției.
• Atribuirea fiecărei locații unui anumit cluster.
• Calcularea distanțelor de la fiecare locație și alocarea punctelor clusterului unde distanța este minimă cu priza.
• După o iterație, realocarea punctelor, găsiți centroidul noului cluster format.

De asemenea, algoritmul K-Means Clustering poate fi aplicat la o varietate de aplicații la scari variate. Industria ospitalității, departamentele de investigare a criminalității și redimensionarea imaginii, pentru a numi câteva.

Algoritmul K-Means este implementat folosind multe limbaje precum R , Python, MATLAB etc. În secțiunea următoare, ne vom uita la modul în care se aplică K-Means Clustering MATLAB.

Citiți: Tipuri de funcții în Matlab

Algoritmul K-Means folosind MATLAB

K-Means este un algoritm utilizat pe scară largă, folosit de mulți profesioniști care se ocupă cu știința datelor, învățarea automată, inteligența artificială, criptografia și securitatea cibernetică.

Obiectivul principal al utilizării acestui algoritm este acela de a afla centroidul fiecărui cluster. Datele date unui programator sunt eterogene. Iată codul MATLAB pentru trasarea centrului de centru al fiecărui grup și pentru a atribui coordonatele fiecărui centroid:

Clustering MATLAB

Cod:

rng implicit; % Pentru reproductibilitate

X = [randn(100,2)*0,75+uni (100,2);

randn(100,2)*0,5-uni(100,2)];

opts=statset('Afișare','final');

[idx,C]=kmeans(X,4,'Distance','cityblock','Replicates',5,'Options',opts);

plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12);

stai așa;

plot(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12);

plot(X(idx==3,1),X(idx==3,2),'g.','MarkerSize',12);

plot(X(idx==4,1),X(idx==4,2),'y.','MarkerSize',12);

plot(C(:,1),C(:,2),'Kx','MarkerSize',15,'LineWidth',3);

legenda('Cluster 1','Cluster 2','Cluster 3','Cluster 4','Centroids', 'Locaţie','NW');

title('Cluster Assignments and centroids');

reține;

pentru i=1:size(C, 1)

display(['Centroid ', num2str(i), ': X1 = ', num2str(C(i, 1)), '; X2 = ', num2str(C(i, 2))]);

Sfârșit

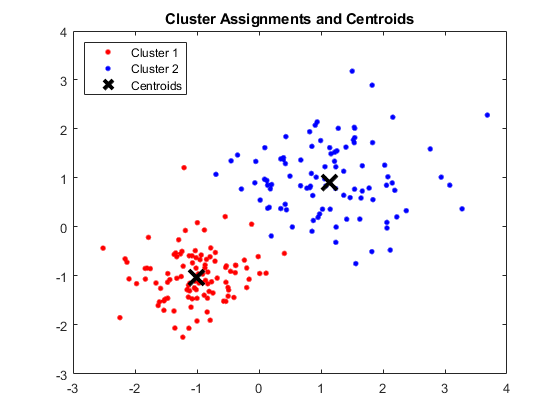
Ieșire:

Fereastra MATLAB care arată patru clustere și centroizii respectivi

Sursa imaginii

Rezultate:

Centroizii obținuți sunt după cum urmează:

1. Valoarea X1 și X2 pentru Centroid 1: 1,3661; 1,7232
2. Valoarea X1 și X2 pentru Centroid 2: -1,015; -1.053
3. Valoarea X1 și X2 pentru Centroid 3: 1,6565; 0,36376
4. Valoarea X1 și X2 pentru Centroid 4: 0,35134; 0,85358

Unele domenii de afaceri în care se poate implementa clustering K-Means

K-means clustering este un algoritm versatil și poate fi folosit pentru multe cazuri de utilizare în afaceri pentru orice tip de grupare. Câteva exemple sunt:

Ø Segregarea comportamentală:

• Diviziune folosind istoricul achizițiilor
• Diviziune folosind activități de aplicație, site web sau platformă
• Identificați imaginea clienților pe baza intereselor acestora
• Crearea profilului cu activități de monitorizare

Ø Scalare imagini

• Comprimarea imaginii folosind Python

Ø Masuratori senzori:

• Detectează tipurile de activitate ale senzorilor de mișcare
• Imagini de grup
• Împărțiți sunetul
• Identificați grupurile de monitorizare a sănătății

Ø Determinați roboți sau anomalii:

• Separați grupurile de activități de roboți
• Faceți un grup de activități valide pentru a curăța detectarea valorii aberante

Ø Clasificarea inventarului:

• Faceți grupuri de inventar în funcție de activitatea de vânzări
• Faceți grupuri de inventar în funcție de valorile de producție

Avantajele grupării K-Means

Există un motiv pentru care profesioniștii de top preferă algoritmul de grupare K-Means. Câteva beneficii pe care le oferă:

• Este un algoritm rapid, robust și mai ușor de înțeles.
• Eficiența finală este relativ mare
• Oferă rezultate fenomenale atunci când seturile de date sunt diferite unele de altele. Pentru valori mai mari ale variabilelor, K-Means funcționează comparativ mai rapid
• Clusterele produse cu K-Means sunt relativ mai strânse decât alte metode de grupare.

Trebuie citit: Tipuri de date MATLAB

Concluzie

Gruparea K-means este o abordare utilizată pe scară largă pentru analiza clusterelor de date. Odată ce obțineți comanda, este mai ușor de înțeles și aplicat și de a oferi rezultate rapid.

Sperăm cu acest articol; v-am putea introduce în această tehnică de analiză. Pentru orice întrebări referitoare la algoritmul K-means, nu ezitați să comentați mai jos.

În plus, dacă acest domeniu de studiu vă interesează, aruncați o privire la programul nostru PG Diploma în Machine Learning și AI , care este special conceput pentru profesioniștii care lucrează, care oferă peste 30 de studii de caz și sarcini, peste 25 de sesiuni de mentorat de la experți din industrie, 10 mâini practice. pe Capstone Projects, peste 450 de ore de asistență pentru învățare și plasare.

Ce este gruparea K Means în învățarea automată?

Acesta este un algoritm de grupare popular utilizat în învățarea automată nesupravegheată. Algoritmul K Means funcționează pe principiul identificării aleatoare a centroizilor K. De la pasul următor, algoritmul încearcă să maximizeze distanța totală în cadrul clusterului și, de asemenea, să minimizeze distanța totală dintre cluster. Algoritmul K Means este o abordare iterativă. În fiecare iterație, selectează K Mediile din setul curent de centroizi. Algoritmul atribuie apoi fiecare observație la cea mai apropiată medie K. Distanța dintre două grupuri este calculată pe baza distanței dintre cele mai apropiate două observații. Centroidul unui cluster este definit ca media tuturor observațiilor din cluster.

Care sunt limitările algoritmului de grupare K Means?

Există câteva limitări ale K Means de care veți dori să țineți cont atunci când îl utilizați. K Means nu este robust pentru valori aberante. Algoritmul K Means funcționează bine numai atunci când toate punctele dvs. de date sunt aproximativ la aceeași distanță de centru. Dacă unele dintre punctele dvs. de date sunt departe de centru, acest lucru va influența alocarea altor puncte de date către clustere. K Means nu garantează o soluție unică. Dacă aveți mai mult de un cluster de puncte, nu există nicio garanție că K Means va returna același număr de clustere de fiecare dată când algoritmul este rulat. K Mijloacele converge lent. Algoritmul converge foarte lent, chiar și pe seturi de date mici.

Care sunt avantajele grupării K Means?

Este eficient atât pentru dimensiuni unice, cât și pentru mai multe dimensiuni. Este aplicabil atât în ​​două cât și în trei dimensiuni. Este deosebit de util în situațiile în care există multe clustere. Clusterele sunt obținute la mijlocul punctelor de date. Se calculează o valoare medie pentru fiecare grup. Fiecare punct este împărțit la abaterea standard și apoi este comparat cu valoarea medie. Valoarea medie și abaterea standard sunt calculate pentru toate grupurile și punctele.