K significa clustering Matlab [con codice sorgente]

Il clustering K-means è una delle tecniche più comunemente utilizzate dai professionisti dei dati. A causa dell'efficacia dell'algoritmo, è richiesto da numerose industrie in varie applicazioni.

Il lavoro di un data scientist richiede l'implementazione del Clustering in molte fasi. Molti progetti su larga scala sono attualmente basati sull'algoritmo di clustering e hanno drasticamente alzato il livello della domanda dei professionisti della scienza dei dati.

Uno di questi algoritmi è il clustering K-means, che è l'idea alla base di questo articolo e della sua implementazione con il codice sorgente MATLAB.

Prima di approfondire l'argomento, diamo una rapida occhiata a cos'è il Clustering, il suo significato e come può essere implementato nella vita reale. Entro la fine del post, scoprirai quanto sia cruciale questo algoritmo per comprendere i dati in grandi insiemi.

Che cos'è il clustering?

I dati sono il componente più critico per qualsiasi applicazione e un cluster non è altro che un accumulo di punti dati simili combinati. Come il nome definisce chiaramente, il clustering è il processo di divisione di una grossa porzione di dati in sottogruppi o solo cluster in base al modello di dati.

Nell'apprendimento automatico, il clustering viene applicato quando non sono disponibili dati predefiniti. L'obiettivo finale è raggruppare i dati in classi con elevata somiglianza intra-classe.

Il clustering viene utilizzato per esplorare i dati. Alcuni esempi di vita reale in cui può essere utilizzato sono nella segmentazione del mercato per trovare clienti con comportamenti simili, segmentazione/compressione di immagini, raggruppamento di documenti con più argomenti, ecc.

È un passaggio necessario prima dell'elaborazione dei dati per identificare gruppi omogenei per la costruzione di modelli supervisionati. Il clustering K-Means è un algoritmo di apprendimento non supervisionato poiché dobbiamo cercare dati per integrare osservazioni simili e formare gruppi distinti.

Diamo un'occhiata all'algoritmo K-Means , che è uno degli algoritmi di clustering più applicati e più semplici.

Cluster di mezzi K

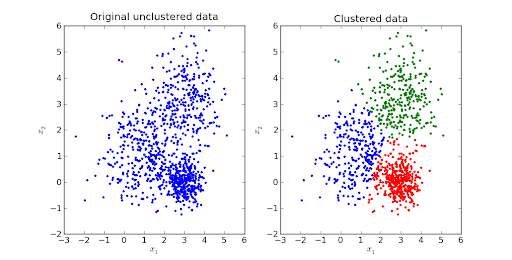
Fonte immagine

Il clustering K-means è uno degli algoritmi di apprendimento automatico senza supervisione più desiderati.

Gli algoritmi non supervisionati traggono conclusioni dai set di dati utilizzando vettori di input senza fare riferimento ai risultati etichettati.

È un algoritmo iterativo basato sulla distanza o sul centroide che separa il set di dati in K sottogruppi distinti (cluster) in cui ogni punto dati appartiene a un gruppo . La somiglianza dei punti dati intra-cluster viene aumentata e la distanza tra i cluster viene mantenuta ottimale.

La distanza tra i punti dati e il baricentro del cluster viene mantenuta al minimo, come la distanza euclidea. In K-Means, ogni cluster è collegato a un centroide. L'obiettivo principale è ridurre al minimo le distanze tra i punti e il rispettivo centroide del cluster.

Come funziona il clustering K-Means?

Poiché il processo di clustering implica l'esecuzione di diverse iterazioni, l'algoritmo K-Means ha un modo unico di lavorare. Ecco una spiegazione passo passo del suo funzionamento:

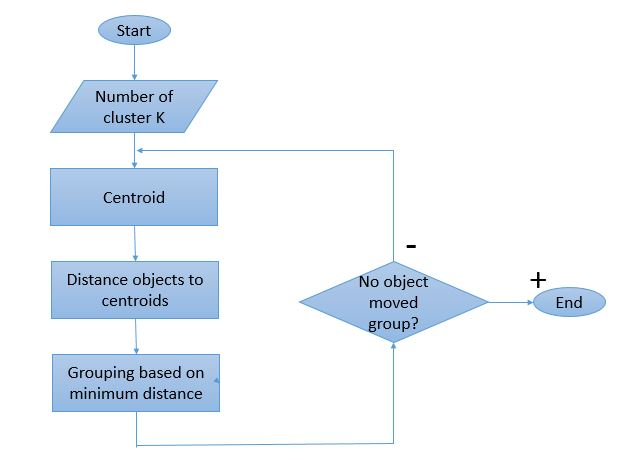
Fonte immagine

Passaggio 1: inizialmente, definire il numero di cluster ' Passaggio 2: inizializza punti dati K casuali come centroidi per ciascun cluster.

Se sono presenti 2 cluster, il valore di 'K' sarà 2.

Passaggio 3: eseguire diverse iterazioni finché i punti dati assegnati ai cluster non cambiano.

Passaggio 4: calcola la somma della distanza al quadrato tra i punti dati e i centroidi.

Passaggio 5: allocare ciascun punto dati al cluster più vicino (centroide) per ridurre al minimo la distanza.

Passaggio 6: prendi una media dei centroidi dei cluster che appartengono l'uno all'altro.

Questo è un singolo processo di iterazione eseguito per calcolare il centroide e assegnare i punti al cluster in base alla loro distanza dal centroide. Una volta definiti tutti i centroidi, il processo viene interrotto.

Un esempio illustrativo che illustra l'implementazione del clustering K-Means

Dichiarazione: McDonald's, una delle famose catene alimentari, vuole aprire una catena di punti vendita in tutta la California e vuole scoprire i luoghi che porteranno loro il massimo reddito.

Cosa ha già McDonald's?

Ø Una forte presenza di e-commerce

Ø Dati cliente online per l'analisi delle posizioni da cui vengono effettuati frequentemente gli ordini

Possibili sfide che potrebbero affrontare

• Analizzare le aree da cui vengono effettuati gli ordini di frequente.
• Scopri quanti punti vendita aprire in zona
• Individua le posizioni dei punti vendita all'interno di tutte le aree per mantenere una distanza minima tra il negozio e i punti di consegna.

Tutti questi punti richiedono molta analisi e matematica su cui lavorare.

Come può essere utilizzato qui il metodo di clustering dei mezzi K?

Con un valore predefinito di K, l'algoritmo K-mean può essere implementato nei seguenti passaggi:

• Identificazione delle posizioni dei negozi con K Partizione di oggetti in K sottoinsiemi non vuoti.
• Determinazione dei centroidi del cluster della partizione.
• Assegnazione di ciascuna posizione a un cluster specifico.
• Calcolare le distanze da ciascuna posizione e assegnare punti al cluster in cui la distanza è minima con l'uscita.
• Dopo un'iterazione, riassegnando i punti, trova il baricentro del nuovo cluster formato.

Allo stesso modo, l'algoritmo K-Means Clustering può essere applicato a una varietà di applicazioni su scale diverse. L'industria dell'ospitalità, i dipartimenti investigativi sulla criminalità e il ridimensionamento delle immagini, solo per citarne alcuni.

L'algoritmo K-Means è implementato utilizzando molti linguaggi come R , Python, MATLAB, ecc. Nella prossima sezione, vedremo come viene applicato il Clustering K-Means MATLAB.

Leggi: Tipi di funzioni in Matlab

Algoritmo K-Means utilizzando MATLAB

K-Means è un algoritmo ampiamente utilizzato da molti professionisti che si occupano di scienza dei dati, apprendimento automatico, intelligenza artificiale, crittografia e sicurezza informatica.

L'obiettivo principale dell'utilizzo di questo algoritmo è scoprire il baricentro di ciascun cluster. I dati forniti a un programmatore sono eterogenei. Ecco il codice MATLAB per tracciare il baricentro di ciascun cluster e assegnare le coordinate di ciascun centroide:

Clustering MATLAB

Codice:

valore predefinito; % Per la riproducibilità

X = [randn(100,2)*0,75+ones(100,2);

randn(100,2)*0,5-ones(100,2)];

opts=statset('Display','final');

[idx,C]=kmeans(X,4,'Distanza','cityblock','Replica',5,'Opzioni',opts);

plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12);

aspettare;

plot(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12);

plot(X(idx==3,1),X(idx==3,2),'g.','MarkerSize',12);

plot(X(idx==4,1),X(idx==4,2),'y.','MarkerSize',12);

plot(C(:,1),C(:,2),'Kx','MarkerSize',15,'LineWidth',3);

legend('Cluster 1′,'Cluster 2′,'Cluster 3′,'Cluster 4′,'Centroids', 'Location','NW');

title('Assegnazioni cluster e centroidi');

tenere a bada;

for i=1:dimensione(C, 1)

display(['Centroid ', num2str(i), ': X1 = ', num2str(C(i, 1)), '; X2 = ', num2str(C(i, 2))]);

fine

Produzione:

Finestra MATLAB che mostra quattro cluster e rispettivi centroidi

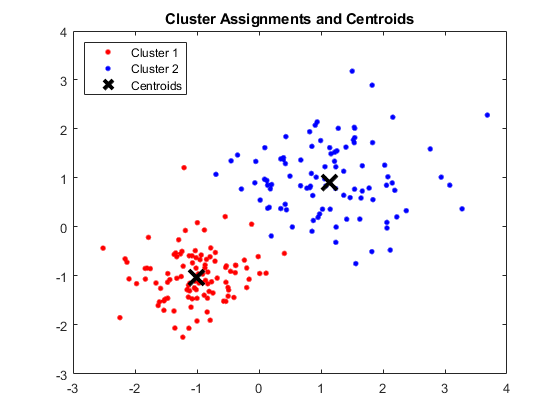
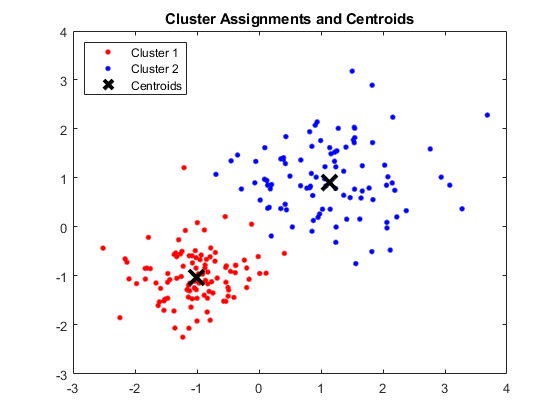
Fonte immagine

Risultati:

I centroidi ottenuti sono i seguenti:

1. Il valore di X1 e X2 per il baricentro 1: 1,3661; 1.7232
2. Il valore di X1 e X2 per Centroid 2: -1,015; -1.053
3. Il valore di X1 e X2 per Centroid 3: 1,6565; 0,36376
4. Il valore di X1 e X2 per Centroid 4: 0,35134; 0,85358

Alcune aree di business in cui è possibile implementare il clustering K-Means

Il clustering K-means è un algoritmo versatile e può essere utilizzato per molti casi d'uso aziendali per qualsiasi tipo di raggruppamento. Alcuni esempi sono:

Ø Segregazione comportamentale:

• Divisione utilizzando la cronologia degli acquisti
• Divisione utilizzando le attività dell'applicazione, del sito Web o della piattaforma
• Identificare l'immagine dei clienti in base ai loro interessi
• Creazione profilo con attività di monitoraggio

Ø Ridimensionamento immagine

• Compressione delle immagini tramite Python

Ø Misure del sensore:

• Rileva i tipi di attività dei sensori di movimento
• Immagini di gruppo
• Dividi l'audio
• Individua i gruppi di monitoraggio della salute

Ø Determinare bot o anomalie:

• Separare i gruppi di attività dai bot
• Crea un gruppo di attività valide per ripulire il rilevamento dei valori anomali

Ø Classificazione dell'inventario:

• Crea gruppi di inventario per attività di vendita
• Crea gruppi di inventario in base alle metriche di produzione

Vantaggi del clustering delle medie K

C'è un motivo per cui i migliori professionisti preferiscono l'algoritmo di clustering K-Means. Alcuni vantaggi che offre:

• È un algoritmo veloce, robusto e di facile comprensione.
• L'efficienza finale è relativamente alta
• Offre risultati fenomenali quando i set di dati sono diversi l'uno dall'altro. Per valori di variabili più elevati, K-Means funziona in modo relativamente più rapido
• I cluster prodotti con K-Means sono relativamente più stretti rispetto ad altri metodi di clustering.

Deve leggere: Tipi di dati MATLAB

Conclusione

Il clustering K-means è un approccio ampiamente utilizzato per l'analisi dei cluster di dati. Una volta acquisito il comando, è più facile capire e applicare e fornire risultati rapidamente.

Speriamo con questo articolo; potremmo presentarvi questa tecnica di analisi. Per qualsiasi domanda relativa all'algoritmo K-mean, non esitare a commentare di seguito.

Inoltre, se questo campo di studio ti interessa, dai un'occhiata al nostro programma PG Diploma in Machine Learning e AI che è appositamente curato per i professionisti che lavorano che offrono oltre 30 casi di studio e incarichi, oltre 25 sessioni di tutoraggio da esperti del settore, 10 mani pratiche- su Capstone Projects, oltre 450 ore di apprendimento e assistenza al collocamento.

Che cos'è il clustering K Means nell'apprendimento automatico?

Questo è un popolare algoritmo di clustering utilizzato nell'apprendimento automatico non supervisionato. L'algoritmo K Means funziona sul principio dell'identificazione dei centroidi K in modo casuale. Dal passaggio successivo, l'algoritmo cerca di massimizzare la distanza complessiva all'interno del cluster e anche di ridurre al minimo la distanza complessiva tra i cluster. L'algoritmo K Means è un approccio iterativo. In ogni iterazione, seleziona le medie K dall'insieme corrente di centroidi. L'algoritmo assegna quindi ogni osservazione alla media K più vicina. La distanza tra due cluster viene calcolata in base alla distanza tra le due osservazioni più vicine. Il centroide di un cluster è definito come la media di tutte le osservazioni nel cluster.

Quali sono i limiti dell'algoritmo di clustering K Means?

Ci sono alcune limitazioni di K Means che vorrai tenere a mente quando lo usi. K Means non è robusto per i valori anomali. L'algoritmo delle medie K funziona bene solo quando tutti i punti dati sono approssimativamente alla stessa distanza dal centroide. Se alcuni dei tuoi punti dati sono lontani dal centroide, ciò influenzerà l'assegnazione di altri punti dati ai cluster. K Mezzi non garantisce una soluzione unica. Se si dispone di più di un cluster di punti, non vi è alcuna garanzia che K Means restituirà lo stesso numero di cluster ogni volta che viene eseguito l'algoritmo. K Significa converge lentamente. L'algoritmo converge molto lentamente, anche su piccoli set di dati.

Quali sono i vantaggi del clustering K Means?

È efficace sia per dimensioni singole che multiple. È applicabile sia in due che in tre dimensioni. È particolarmente utile in situazioni in cui sono presenti molti cluster. I cluster sono ottenuti nel punto medio dei punti dati. Viene calcolato un valore medio per ciascun cluster. Ogni punto viene diviso per la deviazione standard e quindi confrontato con il valore medio. Il valore medio e la deviazione standard vengono calcolati per tutti i cluster e punti.