快速排序算法解釋[示例]

快速排序基於分治算法的概念，這也是合併排序中使用的概念。 不同之處在於，在快速排序中，最重要或最重要的工作是在將數組分區（或劃分）為子數組時完成的，而在合併排序的情況下，所有主要工作都發生在合併子數組期間。 對於快速排序，合併步驟無關緊要。

快速排序也稱為分區交換排序。 該算法將給定的數字數組分為三個主要部分：

1. 小於樞軸元素的元素
2. 樞軸元素
3. 大於樞軸元素的元素

可以通過多種不同方式從給定的數字中選擇樞軸元素：

1. 選擇第一個元素
2. 選擇最後一個元素（顯示示例）
3. 選擇任何隨機元素
4. 選擇中位數

例如：在數組{51, 36, 62, 13, 16, 7, 5, 24}中，我們將24作為樞軸（最後一個元素）。 所以在第一遍之後，列表會變成這樣。

{5 7 16 13 24 62 36 51}

因此，在第一次遍歷之後，對數組進行排序，使得小於所選樞軸的所有元素都位於其左側，而所有大於所選樞軸的元素位於其右側。 樞軸最終位於它應該在數組的排序版本中的位置。 現在子數組{5 7 16 13}和{62 36 51}被視為兩個獨立的數組，並且將對其應用相同的遞歸邏輯，並且我們將繼續這樣做，直到對整個數組進行排序。

另請閱讀：數據結構中的堆排序

它是如何工作的？

這些是快速排序算法中遵循的步驟：

1. 我們選擇我們的樞軸作為最後一個元素，並且我們第一次開始對數組進行分區（或劃分）。
2. 在這個分區算法中，數組被分成 2 個子數組，這樣所有小於樞軸的元素都將位於樞軸的左側，而所有大於樞軸的元素將位於其右側。
3. 並且樞軸元素將處於其最終排序位置。
4. 左右子數組中的元素不必排序。
5. 然後我們遞歸地選擇左右子數組，並通過在子數組中選擇一個樞軸對它們中的每一個執行分區，並重複這些步驟。

下面顯示了該算法在 C++ 代碼中的工作方式，使用示例數組。

void QuickSort(int a[], int low, int high)

{

如果（高<低）

返回;

int p=分區（a，低，高）；

快速排序(a,low,p-1);

快速排序(a,p+1,high);

}

int 分區（int a[]，int 低，int 高）

{

詮釋樞軸=一個[高]；

詮釋我=低；

for(int j=low;j<high;j++)

{

if(a[j]<=pivot)

{

交換(&a[j],&a[i]);

我++；

}

}

交換(&a[i],&a[high]);

返回我；

}

主函數（）

{

int arr[]={6,1,5,2,4,3};

快速排序（arr,0,5）；

cout<<"排序後的數組為：";

for(int i=0; i<6; i++)

cout<<arr[i]<<" ";

返回0；

}

下面是快速排序如何對給定數組進行排序的圖示。

假設初始輸入數組是：

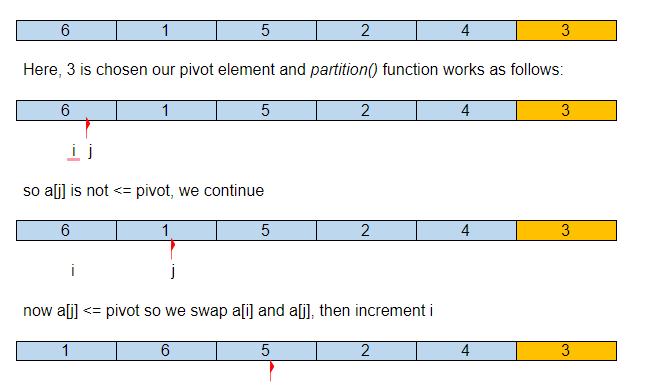
因此，在我們的第一個分區之後，樞軸元素在排序數組中的正確位置，其所有較小的元素在左側，較大的元素在右側。

現在QuickSort()將遞歸調用子數組 {1,2} 和 {6,4,5} 並繼續直到數組排序。

必讀：你應該知道的人工智能算法類型

複雜性分析

Ω 最佳案例時間複雜度： Ω Θ 平均時間複雜度： Θ O(n 最壞情況時間複雜度： O(n 如果分區導致幾乎相等的子數組，那麼運行時間是最好的，時間複雜度為 O(n*log n)。

最壞的情況發生在元素已經排序的數組中，並且選擇樞軸作為最後一個元素。 在這裡，分區給出了不平衡的子數組，其中所有元素都已經小於樞軸，因此在其左側，而右側沒有元素。

O(n*log n)O(n*log n)

結論

快速排序是一種基於比較的算法，它並不穩定。 可以進行的一個小優化是先為較小的子數組調用遞歸QuickSort()函數，然後再為較大的子數組調用。

總體而言，快速排序是一種高效的排序技術，在較小數組的情況下可以提供比合併排序更好的性能。

如果您熱衷於了解更多信息，請查看 upGrad 和 IIIT-B 的機器學習和 AI 計劃的 PG 文憑。