クイックソートアルゴリズムの説明[例付き]

クイックソートは、マージソートで使用される概念でもある分割統治アルゴリズムの概念に基づいています。 違いは、クイックソートでは、配列をサブ配列に分割（または分割）するときに最も重要または重要な作業が行われるのに対し、マージソートの場合は、すべての主要な作業がサブ配列のマージ中に行われることです。 クイックソートの場合、結合ステップは重要ではありません。

クイックソートは、パーティション交換ソートとも呼ばれます。 このアルゴリズムは、指定された数値の配列を3つの主要部分に分割します。

1. ピボット要素よりも小さい要素
2. ピボット要素
3. ピボット要素より大きい要素

ピボット要素は、さまざまな方法で指定された数値から選択できます。

1. 最初の要素を選択する
2. 最後の要素の選択（例を示します）
3. ランダムな要素を選択する
4. 中央値の選択

例：配列{51、36、62、13、16、7、5、24}では、 24をピボット（最後の要素）とします。 したがって、最初のパスの後、リストは次のように変更されます。

{5 7 16 13 24 62 36 51}

したがって、最初のパスの後、選択したピボットよりも小さいすべての要素が左側にあり、すべての大きい要素が右側にあるように、配列が並べ替えられます。 ピボットは最終的に、配列のソートされたバージョンにあるはずの位置にあります。 これで、サブ配列{5 7 1613}と{623651}は2つの別個の配列と見なされ、同じ再帰ロジックがそれらに適用され、完全な配列が並べ替えられるまでこれを続けます。

また読む：データ構造のヒープソート

それはどのように機能しますか？

クイックソートアルゴリズムで実行される手順は次のとおりです。

1. 最後の要素としてピボットを選択し、初めて配列の分割（または分割）を開始します。
2. この分割アルゴリズムでは、配列は2つのサブ配列に分割され、ピボットよりも小さいすべての要素がピボットの左側に配置され、ピボットよりも大きいすべての要素がピボットの右側に配置されます。
3. そして、ピボット要素は最終的にソートされた位置になります。
4. 左右のサブ配列の要素を並べ替える必要はありません。
5. 次に、左右のサブアレイを再帰的に選択し、サブアレイのピボットを選択してそれぞれでパーティション分割を実行し、同じ手順を繰り返します。

以下に示すのは、配列例を使用して、C++コードでアルゴリズムがどのように機能するかです。

void QuickSort（int a []、int low、int high）

{{

if（高<低）

戻る;

int p = partition（a、low、high）;

QuickSort（a、low、p-1）;

QuickSort（a、p + 1、high）;

}

intパーティション（int a []、int low、int high）

{{

intピボット=a[高];

int i = low;

for（int j = low; j <high; j ++）

{{

if（a [j] <=ピボット）

{{

swap（＆a [j]、＆a [i]）;

i ++;

}

}

swap（＆a [i]、＆a [high]）;

iを返します。

}

int main（）

{{

int arr [] = {6,1,5,2,4,3};

QuickSort（arr、0,5）;

cout <<”ソートされた配列は次のとおりです：“;

for（int i = 0; i <6; i ++）

cout << arr [i] <<”“;

0を返します。

}

以下は、指定された配列をクイックソートでソートする方法を図で表したものです。

初期入力配列が次のとおりであると仮定します。

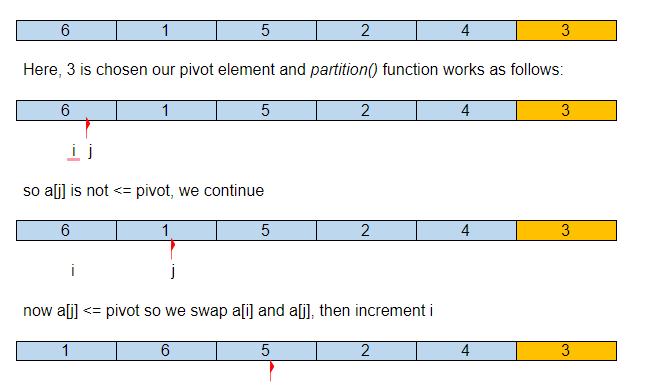
したがって、最初のパーティションの後、ピボット要素は並べ替えられた配列の正しい位置にあり、小さい要素はすべて左側にあり、大きい要素は右側にあります。

これで、 QuickSort （）がサブ配列{1,2}と{6,4,5}に対して再帰的に呼び出され、配列がソートされるまで続行されます。

必読：知っておくべきAIアルゴリズムの種類

複雑さの分析

Ω ベストケースの時間計算量： Ω Θ 平均時間計算量： Θ O(n 最悪の場合の時間計算量： O（n パーティショニングによってサブアレイがほぼ等しくなる場合は、実行時間が最適であり、時間計算量はO（n * log n）です。

最悪のケースは、要素がすでにソートされており、ピボットが最後の要素として選択されている場合の配列で発生します。 ここで、パーティショニングは不均衡なサブアレイを提供します。すべての要素はすでにピボットよりも小さく、したがって左側にあり、右側には要素がありません。

O(n*log n)O（n * log n）

結論

クイックソートは比較ベースのアルゴリズムであり、安定していません。 実行できる小さな最適化は、最初に小さいサブアレイに対して再帰的なQuickSort（）関数を呼び出し、次に大きいサブアレイに対して呼び出すことです。

全体として、クイックソートは非常に効率的なソート手法であり、配列が小さい場合はマージソートよりも優れたパフォーマンスを提供できます。

詳細を知りたい場合は、upGrad＆IIIT-Bの機械学習とAIプログラムのPGディプロマをご覧ください。