Wyjaśnienie algorytmu Quicksort [z przykładem]

Szybkie sortowanie opiera się na koncepcji algorytmu Dziel i zwyciężaj , która jest również koncepcją stosowaną w sortowaniu przez scalanie. Różnica polega na tym, że w szybkim sortowaniu najważniejsza lub najważniejsza praca jest wykonywana podczas partycjonowania (lub dzielenia) tablicy na podtablice, podczas gdy w przypadku sortowania przez scalanie cała główna praca odbywa się podczas łączenia podtablic. W przypadku szybkiego sortowania etap łączenia jest nieistotny.

Szybkie sortowanie jest również nazywane sortowaniem z wymianą partycji . Algorytm ten dzieli daną tablicę liczb na trzy główne części:

1. Elementy mniejsze niż element obrotowy
2. Element obrotowy
3. Elementy większe niż element obrotowy

Element Pivot można wybrać z podanych liczb na wiele różnych sposobów:

1. Wybór pierwszego elementu
2. Wybór ostatniego elementu (pokazany przykład)
3. Wybór dowolnego elementu losowego
4. Wybór mediany

Na przykład: W tablicy {51, 36, 62, 13, 16, 7, 5, 24} bierzemy 24 jako piwot (ostatni element). Więc po pierwszym przejściu lista zostanie zmieniona w ten sposób.

{5 7 16 13 24 62 36 51}

Stąd po pierwszym przejściu tablica jest sortowana w taki sposób, że wszystkie elementy mniejsze od wybranego elementu obrotowego znajdują się po jej lewej stronie, a wszystkie większe po prawej stronie. Oś znajduje się w końcu w pozycji, w której powinien znajdować się w posortowanej wersji tablicy. Teraz podtablice {5 7 16 13} i {62 36 51} są uważane za dwie oddzielne tablice i zostanie na nich zastosowana ta sama logika rekurencyjna i będziemy to robić, dopóki cała tablica nie zostanie posortowana.

Przeczytaj także: Sortowanie sterty w strukturze danych

Jak to działa?

Oto kroki wykonywane w algorytmie szybkiego sortowania:

1. Jako ostatni element wybieramy naszego pivota i po raz pierwszy zaczynamy partycjonować (lub dzielić) tablicę.
2. W tym algorytmie partycjonowania tablica jest podzielona na 2 podtablice w taki sposób, że wszystkie elementy mniejsze niż oś znajdują się po lewej stronie osi, a wszystkie elementy większe niż oś po prawej stronie.
3. A element obrotowy znajdzie się w końcowej, posortowanej pozycji.
4. Elementy w lewej i prawej podtablicy nie muszą być sortowane.
5. Następnie rekurencyjnie wybieramy lewą i prawą podtablicę i przeprowadzamy partycjonowanie na każdej z nich, wybierając oś w podtablicach, a kroki są powtarzane dla tego samego.

Poniżej pokazano, jak działa algorytm w kodzie C++ na przykładowej tablicy.

void QuickSort(int a[], int niski, int wysoki)

{

jeśli(wysoki<niski)

powrót;

int p= partycja(a,niski,wysoki);

Szybkie sortowanie(a,niskie,p-1);

Szybkie sortowanie(a,p+1,wysokie);

}

int partycja(int a[], int niski, int wysoki)

{

int pivot=a[wysoki];

int i=niski;

for(int j=niski; j<wysoki; j++)

{

if(a[j]<=pivot)

{

swap(&a[j],&a[i]);

i++;

}

}

swap(&a[i],&a[wysoki]);

powrót ja;

}

int main()

{

wewn arr[]={6,1,5,2,4,3};

Szybkie sortowanie(arr,0,5);

cout<<”Posortowana tablica to: “;

for(int i=0; i<6; i++)

cout<<arr[i]<<” “;

zwróć 0;

}

Poniżej znajduje się obrazowa reprezentacja tego, jak szybkie sortowanie posortuje daną tablicę.

Załóżmy, że początkowa tablica wejściowa to:

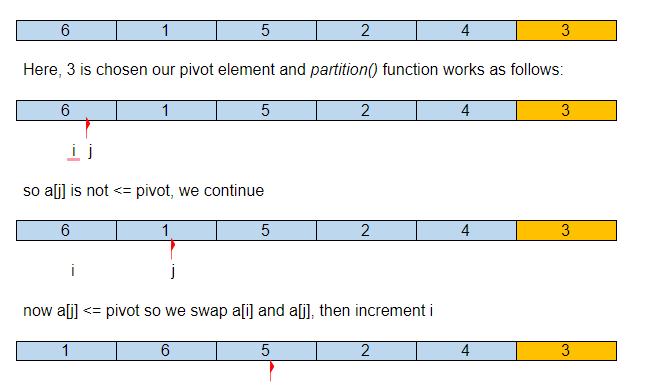
Tak więc po naszym pierwszym podziale element przestawny znajduje się we właściwym miejscu w posortowanej tablicy, ze wszystkimi mniejszymi elementami po lewej stronie i większymi po prawej stronie.

Teraz funkcja QuickSort() będzie wywoływana rekurencyjnie dla podtablic {1,2} i {6,4,5} i będzie kontynuowana aż do posortowania tablicy.

Musisz przeczytać: rodzaje algorytmów AI, które powinieneś znać

Analiza złożoności

Ω Złożoność czasowa najlepszego przypadku: Ω Θ Średnia złożoność czasu: Θ O(n Złożoność czasowa najgorszego przypadku: O(n Jeśli partycjonowanie prowadzi do prawie równych podtablic, wtedy czas działania jest najlepszy, ze złożonością czasową wynoszącą O(n*log n).

Najgorszy przypadek ma miejsce w przypadku tablic z przypadkami, w których elementy są już posortowane, a jako ostatni element jest wybrany element przestawny. Tutaj podział daje niezrównoważone podmacierze, w których wszystkie elementy są już mniejsze niż oś, a więc po jego lewej stronie, a żadnych elementów po prawej stronie.

O(n*log n) O(n*log n)

Wniosek

Quicksort jest algorytmem opartym na porównaniach i nie jest stabilny . Niewielką optymalizacją, którą można zrobić, jest wywołanie rekurencyjnej funkcji QuickSort() najpierw dla mniejszej podtablicy, a następnie dla większej podtablicy.

Ogólnie rzecz biorąc, szybkie sortowanie to wysoce wydajna technika sortowania, która może zapewnić lepszą wydajność niż sortowanie przez scalanie w przypadku mniejszych tablic.

Jeśli chcesz dowiedzieć się więcej, sprawdź dyplom PG upGrad i IIIT-B w zakresie uczenia maszynowego i programu AI.