Explication de l'algorithme de tri rapide [avec exemple]

Quick Sort est basé sur le concept de l' algorithme Divide and Conquer , qui est également le concept utilisé dans Merge Sort. La différence est que, dans le tri rapide, le travail le plus important ou le plus significatif est effectué lors du partitionnement (ou de la division) du tableau en sous-tableaux, tandis qu'en cas de tri par fusion, tout le travail majeur se produit lors de la fusion des sous-tableaux. Pour un tri rapide, l'étape de combinaison est insignifiante.

Le tri rapide est également appelé tri par échange de partition . Cet algorithme divise le tableau de nombres donné en trois parties principales :

1. Éléments inférieurs à l'élément pivot
2. Elément pivotant
3. Éléments supérieurs à l'élément pivot

L'élément pivot peut être choisi parmi les nombres donnés de différentes manières :

1. Choisir le premier élément
2. Choix du dernier élément (exemple illustré)
3. Choisir n'importe quel élément aléatoire
4. Choisir la médiane

Par exemple : Dans le tableau {51, 36, 62, 13, 16, 7, 5, 24} , on prend 24 comme pivot (dernier élément). Ainsi, après le premier passage, la liste sera modifiée comme ceci.

{5 7 16 13 24 62 36 51}

Par conséquent, après la première passe, le tableau est trié de telle sorte que tous les éléments inférieurs au pivot choisi soient sur son côté gauche et tous les éléments supérieurs sur son côté droit. Le pivot est finalement à la position où il est supposé être dans la version triée du tableau. Maintenant, les sous-tableaux {5 7 16 13} et {62 36 51} sont considérés comme deux tableaux séparés, et la même logique récursive leur sera appliquée, et nous continuerons à le faire jusqu'à ce que le tableau complet soit trié.

Lisez également : Tri par tas dans la structure de données

Comment ça marche?

Voici les étapes suivies dans l'algorithme de tri rapide :

1. Nous choisissons notre pivot comme dernier élément, et nous commençons à partitionner (ou diviser) le tableau pour la première fois.
2. Dans cet algorithme de partitionnement, le tableau est divisé en 2 sous-tableaux de sorte que tous les éléments plus petits que le pivot seront du côté gauche du pivot et tous les éléments plus grands que le pivot seront du côté droit de celui-ci.
3. Et l'élément pivot sera à sa position triée finale.
4. Les éléments des sous-tableaux gauche et droit n'ont pas besoin d'être triés.
5. Ensuite, nous sélectionnons récursivement les sous-réseaux gauche et droit, et nous effectuons un partitionnement sur chacun d'eux en choisissant un pivot dans les sous-réseaux et les étapes sont répétées pour le même.

Vous trouverez ci-dessous comment l'algorithme fonctionne dans le code C++, en utilisant un exemple de tableau.

void QuickSort(int a[], int low, int high)

{

si (haut < bas)

retourner;

int p= partition(a,low,high);

Tri rapide(a,low,p-1);

Tri rapide(a,p+1,élevé);

}

int partition(int a[], int bas, int haut)

{

int pivot=a[élevé] ;

entier je=faible ;

for(int j=bas; j<haut; j++)

{

si(a[j]<=pivot)

{

échange(&a[j],&a[i]);

je++ ;

}

}

swap(&a[i],&a[high]);

retourner je ;

}

int main()

{

int arr[]={6,1,5,2,4,3} ;

Tri rapide(arr,0,5);

cout<<"Le tableau trié est : " ;

for(int i=0; i<6; i++)

cout<<arr[i]<< » « ;

renvoie 0 ;

}

Vous trouverez ci-dessous une représentation graphique de la façon dont le tri rapide triera le tableau donné.

Supposons que le tableau d'entrée initial est :

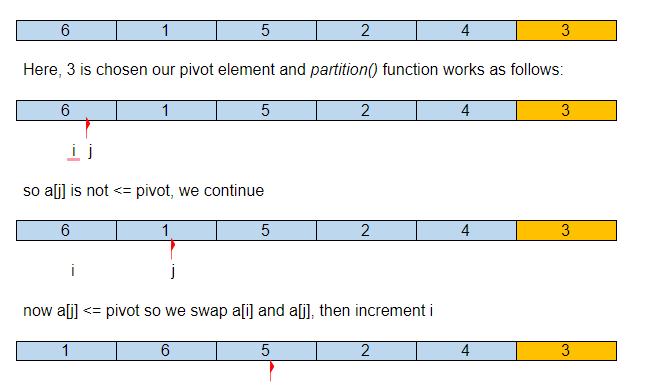
Ainsi, après notre première partition, l'élément pivot est à sa place correcte dans le tableau trié, avec tous ses éléments plus petits à gauche et plus à droite.

Maintenant, QuickSort() sera appelé de manière récursive pour les sous-tableaux {1,2} et {6,4,5} et continuera jusqu'à ce que le tableau soit trié.

Doit lire : Types d'algorithmes d'IA que vous devez connaître

Analyse de complexité

Ω Complexité temporelle dans le meilleur des cas : Ω Θ Complexité temporelle moyenne : Θ O(n Complexité temporelle dans le pire des cas : O(n Si le partitionnement conduit à des sous-réseaux presque égaux, alors le temps d'exécution est le meilleur, avec une complexité temporelle égale à O(n*log n).

Le pire des cas se produit pour les tableaux avec des cas où les éléments sont déjà triés et où pivot est choisi comme dernier élément. Ici, le partitionnement donne des sous-tableaux déséquilibrés, où tous les éléments sont déjà plus petits que le pivot et donc sur son côté gauche, et aucun élément sur le côté droit.

O(n*log n) O(n*log n)

Conclusion

Quicksort est un algorithme basé sur la comparaison et il n'est pas stable . Une petite optimisation qui peut être faite consiste à appeler la fonction récursive QuickSort() pour le plus petit sous-tableau d'abord, puis le plus grand sous-tableau.

Dans l'ensemble, le tri rapide est une technique de tri très efficace qui peut offrir de meilleures performances que le tri par fusion dans le cas de tableaux plus petits.

Si vous souhaitez en savoir plus, consultez le programme de diplôme PG upGrad & IIIT-B en apprentissage automatique et IA.