Quicksort Algoritmasının Açıklaması [Örnekle]

Hızlı Sıralama, Merge Sort'ta da kullanılan kavram olan Böl ve Yönet algoritması kavramına dayanmaktadır . Aradaki fark, hızlı sıralamada en önemli veya önemli iş diziyi alt dizilere ayırırken (veya bölerken) yapılırken, birleştirme sıralama durumunda tüm büyük iş alt dizileri birleştirirken gerçekleşir . Hızlı sıralama için birleştirme adımı önemsizdir.

Hızlı Sıralama aynı zamanda bölüm değiştirme sıralama olarak da adlandırılır . Bu algoritma, verilen sayı dizisini üç ana bölüme ayırır:

1. Pivot öğeden daha küçük öğeler
2. Pivot öğesi
3. Pivot öğesinden daha büyük öğeler

Pivot eleman, verilen numaralardan birçok farklı şekilde seçilebilir:

1. İlk elemanın seçilmesi
2. Son elemanı seçme (gösterilen örnek)
3. Herhangi bir rastgele öğe seçme
4. medyanı seçmek

Örneğin: {51, 36, 62, 13, 16, 7, 5, 24} dizisinde 24'ü pivot (son eleman) olarak alıyoruz . Yani ilk geçişten sonra liste bu şekilde değişecek.

{5 7 16 13 24 62 36 51}

Bu nedenle, ilk geçişten sonra dizi, seçilen pivottan daha küçük tüm öğeler sol tarafında ve tüm büyük öğeler sağ tarafında olacak şekilde sıralanır. Pivot nihayet dizinin sıralanmış versiyonunda olması gereken konumdadır. Şimdi {5 7 16 13} ve {62 36 51} alt dizileri iki ayrı dizi olarak kabul edilir ve onlara aynı özyinelemeli mantık uygulanacak ve tüm dizi sıralanana kadar bunu yapmaya devam edeceğiz.

Ayrıca Okuyun: Veri Yapısında Yığın Sıralama

O nasıl çalışır?

Hızlı sıralama algoritmasında izlenen adımlar şunlardır:

1. Son eleman olarak pivotumuzu seçiyoruz ve diziyi ilk kez bölmeye (veya bölmeye) başlıyoruz.
2. Bu bölümleme algoritmasında dizi, pivottan daha küçük olan tüm elemanlar pivotun sol tarafında olacak ve pivottan daha büyük olan tüm elemanlar sağ tarafında olacak şekilde 2 alt diziye bölünür.
3. Ve pivot eleman son sıralanmış konumunda olacaktır.
4. Sol ve sağ alt dizilerdeki öğelerin sıralanması gerekmez.
5. Daha sonra yinelemeli olarak sol ve sağ alt dizileri seçiyoruz ve alt dizilerde bir pivot seçerek her biri üzerinde bölümleme yapıyoruz ve adımlar aynı şekilde tekrarlanıyor.

Aşağıda, örnek bir dizi kullanılarak algoritmanın C++ kodunda nasıl çalıştığı gösterilmektedir.

void QuickSort(int a[], int düşük, int yüksek)

{

if(yüksek<düşük)

dönüş;

int p= partition(a,düşük,yüksek);

QuickSort(a,düşük,p-1);

QuickSort(a,p+1,yüksek);

}

int bölümü(int a[], int düşük, int yüksek)

{

int pivot=a[yüksek];

int i=düşük;

for(int j=düşük; j<yüksek; j++)

{

if(a[j]<=pivot)

{

takas(&a[j],&a[i]);

ben++;

}

}

takas(&a[i],&a[yüksek]);

dönüş i;

}

int ana()

{

int dizi[]={6,1,5,2,4,3};

HızlıSırala(dizi,0,5);

cout<<”Sıralanan dizi: “;

for(int i=0; i<6; i++)

cout<<arr[i]<<" ";

0 döndür;

}

Aşağıda, verilen diziyi ne kadar hızlı sıralayacağına dair resimli bir temsil bulunmaktadır.

İlk giriş dizisinin şöyle olduğunu varsayalım:

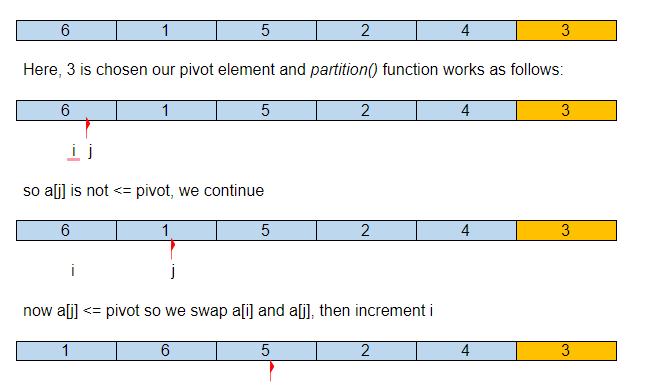
Böylece, ilk bölümümüzden sonra, pivot öğe, tüm küçük öğeleri solda ve daha büyükleri sağda olacak şekilde, sıralanmış dizideki doğru yerindedir.

Şimdi QuickSort() , {1,2} ve {6,4,5} alt dizileri için özyinelemeli olarak çağrılacak ve dizi sıralanana kadar devam edecek.

Mutlaka Okuyun: Bilmeniz Gereken Yapay Zeka Algoritma Türleri

Karmaşıklık Analizi

Ω En İyi Durum Zaman Karmaşıklığı: Ω Θ Ortalama Zaman Karmaşıklığı: Θ O(n En Kötü Durum Zaman Karmaşıklığı: O(n Bölümleme, neredeyse eşit alt dizilere yol açarsa, zaman karmaşıklığı O(n*log n) olarak, çalışma süresi en iyisidir.

En kötü durum, öğelerin zaten sıralandığı ve son öğe olarak pivotun seçildiği durumlara sahip diziler için olur. Burada bölümleme, tüm öğelerin zaten pivottan daha küçük olduğu ve dolayısıyla sol tarafında olduğu ve sağ tarafta hiçbir öğenin bulunmadığı dengesiz alt diziler verir.

O(n*log n) O(n*log n)

Çözüm

Quicksort, karşılaştırmaya dayalı bir algoritmadır ve kararlı değildir . Yapılabilecek küçük bir optimizasyon, önce daha küçük alt dizi ve ardından daha büyük alt dizi için özyinelemeli QuickSort() işlevini çağırmaktır.

Genel olarak, Hızlı Sıralama, daha küçük diziler durumunda Merge Sort'tan daha iyi performans sağlayabilen oldukça verimli bir sıralama tekniğidir.

Daha fazlasını öğrenmek istiyorsanız, yukarıGrad & IIIT-B'nin Makine Öğrenimi ve Yapay Zeka Programındaki PG Diplomasına göz atın.