Algoritmul de sortare rapidă explicat [cu exemplu]

Sortare rapidă se bazează pe conceptul de algoritm Divide and Conquer , care este și conceptul folosit în Merge Sort. Diferența este că, în sortarea rapidă, cea mai importantă sau semnificativă lucrare este făcută în timp ce partiționați (sau împărțiți) matricea în subbary, în timp ce în cazul sortării prin îmbinare, toate lucrările majore au loc în timpul îmbinării subbary-urilor. Pentru sortarea rapidă, pasul de combinare este nesemnificativ.

Sortare rapidă se mai numește și sortare cu schimb de partiții . Acest algoritm împarte matricea dată de numere în trei părți principale:

1. Elemente mai mici decât elementul pivot
2. Element pivot
3. Elemente mai mari decât elementul pivot

Elementul pivot poate fi ales dintre numerele date în mai multe moduri diferite:

1. Alegerea primului element
2. Alegerea ultimului element (exemplu prezentat)
3. Alegerea oricărui element aleatoriu
4. Alegerea medianei

De exemplu: în tabloul {51, 36, 62, 13, 16, 7, 5, 24} , luăm 24 ca pivot (ultimul element). Deci, după prima trecere, lista va fi schimbată astfel.

{5 7 16 13 24 62 36 51}

Prin urmare, după prima trecere, matricea este sortată astfel încât toate elementele mai mici decât pivotul ales să fie pe partea stângă și toate elementele mai mari pe partea dreaptă. Pivotul se află în sfârșit în poziția în care ar trebui să fie în versiunea sortată a matricei. Acum subtabelele {5 7 16 13} și {62 36 51} sunt considerate ca două tablouri separate, și aceeași logică recursivă va fi aplicată asupra lor și vom continua să facem acest lucru până când matricea completă este sortată.

Citiți și: Sortare heap în structura datelor

Cum functioneazã?

Aceștia sunt pașii urmați în algoritmul de sortare rapidă:

1. Alegem pivotul nostru ca ultimul element și începem să partiționăm (sau împărțim) matricea pentru prima dată.
2. În acest algoritm de partiționare, matricea este împărțită în 2 subgrupuri astfel încât toate elementele mai mici decât pivotul vor fi pe partea stângă a pivotului și toate elementele mai mari decât pivotul vor fi pe partea dreaptă a acestuia.
3. Și elementul pivot va fi în poziția finală sortată.
4. Elementele din subbaryurile din stânga și din dreapta nu trebuie să fie sortate.
5. Apoi alegem recursiv sub-tabele din stânga și din dreapta și efectuăm partiționarea pe fiecare dintre ele alegând un pivot în sub-tare și pașii se repetă pentru același lucru.

Mai jos este prezentat cum funcționează algoritmul în codul C++, folosind un exemplu de matrice.

void QuickSort (int a[], int low, int high)

{

dacă (mare < scăzut)

întoarcere;

int p= partition(a,low,high);

QuickSort(a,low,p-1);

QuickSort(a,p+1,high);

}

partiție int (int a[], int low, int high)

{

int pivot=a[high];

int i=scăzut;

for(int j=low; j<high; j++)

{

if(a[j]<=pivot)

{

swap(&a[j],&a[i]);

i++;

}

}

swap(&a[i],&a[high]);

returnează i;

}

int main()

{

int arr[]={6,1,5,2,4,3};

QuickSort(arr,0,5);

cout<<”Matricea sortată este: “;

for(int i=0; i<6; i++)

cout<<arr[i]<<” „;

returnează 0;

}

Mai jos este o reprezentare grafică a modului în care sortarea rapidă va sorta matricea dată.

Să presupunem că matricea inițială de intrare este:

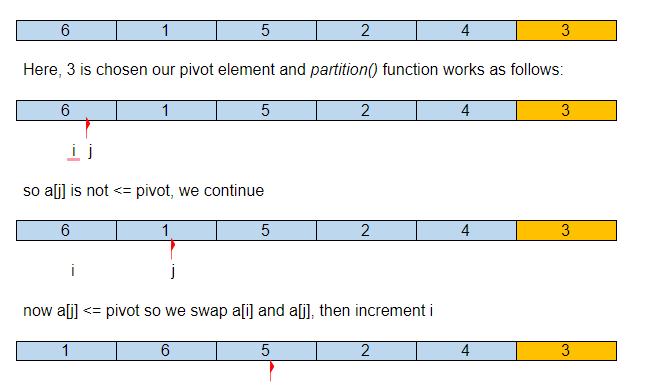
Deci, după prima noastră partiție, elementul pivot este la locul său corect în matricea sortată, cu toate elementele sale mai mici la stânga și mai mari la dreapta.

Acum QuickSort() va fi apelat recursiv pentru sub-tabele {1,2} și {6,4,5} și va continua până când matricea este sortată.

Trebuie citit: Tipuri de algoritmi AI pe care ar trebui să le cunoașteți

Analiza complexității

Ω Complexitatea timpului cel mai bun caz: Ω Θ Complexitatea timpului mediu: Θ O(n Complexitatea timpului cel mai rău caz: O(n Dacă partiționarea duce la subbaryuri aproape egale, atunci timpul de rulare este cel mai bun, cu complexitatea timpului ca O(n*log n).

Cel mai rău caz se întâmplă pentru matrice cu cazuri în care elementele sunt deja sortate, iar pivotul este ales ca ultimul element. Aici, partiționarea dă sub-cadramente dezechilibrate, în care toate elementele sunt deja mai mici decât pivotul și, prin urmare, pe partea stângă, și niciun element pe partea dreaptă.

O(n*log n) O(n*log n)

Concluzie

Quicksort este un algoritm bazat pe comparație și nu este stabil . O mică optimizare care poate fi făcută este să apelați mai întâi funcția recursivă QuickSort() pentru subbarra mai mică și apoi pentru subbarra mai mare.

În general, Quick Sort este o tehnică de sortare extrem de eficientă, care poate oferi performanțe mai bune decât Merge Sort în cazul matricelor mai mici.

Dacă doriți să învățați mai multe, consultați programul PG Diploma în învățare automată și AI a upGrad și IIIT-B.