อธิบายอัลกอริทึม Quicksort [พร้อมตัวอย่าง]
เผยแพร่แล้ว: 2020-12-15Quick Sort ขึ้นอยู่กับแนวคิดของ อัลกอริธึม Divide และ Conquer ซึ่งเป็นแนวคิดที่ใช้ใน Merge Sort ความแตกต่างก็คือ ในการเรียงลำดับอย่างรวดเร็ว งานที่สำคัญที่สุดหรือมีความสำคัญที่สุดจะทำในขณะที่ แบ่งพาร์ติชั่น (หรือแบ่ง) อาเรย์ออกเป็นอาร์เรย์ย่อย ในขณะที่ในกรณีของการเรียงลำดับแบบผสาน งานหลักทั้งหมดจะเกิดขึ้นในระหว่าง การรวม อาร์เรย์ย่อย สำหรับการเรียงลำดับอย่างรวดเร็ว ขั้นตอนการรวมจะไม่มีนัยสำคัญ
Quick Sort เรียกอีกอย่างว่า partition -exchange sort อัลกอริทึมนี้แบ่งอาร์เรย์ของตัวเลขที่กำหนดออกเป็นสามส่วนหลัก:
- องค์ประกอบที่น้อยกว่าองค์ประกอบเดือย
- องค์ประกอบหมุน
- องค์ประกอบที่มากกว่าองค์ประกอบเดือย
คุณสามารถเลือกองค์ประกอบ Pivot จากตัวเลขที่กำหนดได้หลายวิธี:
- การเลือกองค์ประกอบแรก
- การเลือกองค์ประกอบสุดท้าย (ตัวอย่างที่แสดง)
- การเลือกองค์ประกอบสุ่มใด ๆ
- การเลือกค่ามัธยฐาน
ตัวอย่างเช่น: ในอาร์เรย์ {51, 36, 62, 13, 16, 7, 5, 24} เราใช้ 24 เป็น เดือย (องค์ประกอบสุดท้าย) ดังนั้นหลังจากผ่านรอบแรก รายการจะเปลี่ยนไปตามนี้
{5 7 16 13 24 62 36 51}
ดังนั้นหลังจากผ่านครั้งแรก อาร์เรย์จะถูกจัดเรียงเพื่อให้องค์ประกอบทั้งหมดที่น้อยกว่าจุดหมุนที่เลือกอยู่ทางด้านซ้ายและองค์ประกอบที่ใหญ่กว่าทั้งหมดอยู่ทางด้านขวา ในที่สุดเดือยก็อยู่ที่ตำแหน่งที่ควรจะอยู่ในรุ่นที่เรียงลำดับของอาร์เรย์ ตอนนี้อาร์เรย์ย่อย {5 7 16 13} และ {62 36 51} ถือเป็นสองอาร์เรย์ที่แยกจากกัน และตรรกะแบบเรียกซ้ำเดียวกันจะถูกนำมาใช้กับอาร์เรย์เหล่านี้ และเราจะทำเช่นนี้ต่อไปจนกว่าจะจัดเรียงอาร์เรย์ทั้งหมด

อ่านเพิ่มเติม: Heap Sort ในโครงสร้างข้อมูล
สารบัญ
มันทำงานอย่างไร?
เหล่านี้คือขั้นตอนที่ตามมาในอัลกอริธึมการเรียงลำดับอย่างรวดเร็ว:
- เราเลือกเดือยของเราเป็นองค์ประกอบสุดท้าย และเราเริ่มแบ่งพาร์ติชั่น (หรือแบ่ง) อาร์เรย์เป็นครั้งแรก
- ในอัลกอริธึมการแบ่งส่วนนี้ อาร์เรย์แบ่งออกเป็น 2 อาร์เรย์ย่อย ดังนั้นองค์ประกอบทั้งหมดที่เล็กกว่าเดือยจะอยู่ที่ด้านซ้ายของเดือย และองค์ประกอบทั้งหมดที่มากกว่าเดือยจะอยู่ที่ด้านขวา
- และองค์ประกอบเดือยจะอยู่ที่ตำแหน่งการจัดเรียงขั้นสุดท้าย
- ไม่จำเป็นต้องจัดเรียงองค์ประกอบในอาร์เรย์ย่อยด้านซ้ายและขวา
- จากนั้นเราเลือกอาร์เรย์ย่อยด้านซ้ายและขวาซ้ำแล้วซ้ำอีก และเราดำเนินการแบ่งพาร์ติชั่นบนแต่ละรายการโดยเลือกเดือยในอาร์เรย์ย่อยและทำซ้ำขั้นตอนสำหรับสิ่งเดียวกัน
ด้านล่างนี้คือวิธีการทำงานของอัลกอริทึมในโค้ด C++ โดยใช้อาร์เรย์ตัวอย่าง
เป็นโมฆะ QuickSort(int a[], int low, int high)
{
ถ้า(สูง<ต่ำ)
กลับ;
int p= พาร์ทิชัน (a, ต่ำ, สูง);
QuickSort (a, ต่ำ, p-1);
QuickSort(a,p+1,สูง);
}
int พาร์ทิชัน (int a[], int ต่ำ, int สูง)
{
int pivot=a[สูง];
int i=ต่ำ;
สำหรับ (int j=low; j<high; j++)
{
ถ้า(a[j]<=เดือย)
{
swap(&a[j],&a[i]);
ผม++;
}
}
swap(&a[i],&a[สูง]);
กลับฉัน;
}
int หลัก ()
{
int arr[]={6,1,5,2,4,3};
QuickSort(arr,0,5);

cout<<”อาร์เรย์ที่เรียงลำดับคือ: “;
สำหรับ (int i=0; i<6; i++)
ศาล<<arr[i]<<" “;
กลับ 0;
}
ด้านล่างนี้คือการแสดงภาพว่าการเรียงลำดับอย่างรวดเร็วจะเรียงลำดับอาร์เรย์ที่กำหนดอย่างไร
สมมติว่าอาร์เรย์อินพุตเริ่มต้นคือ:
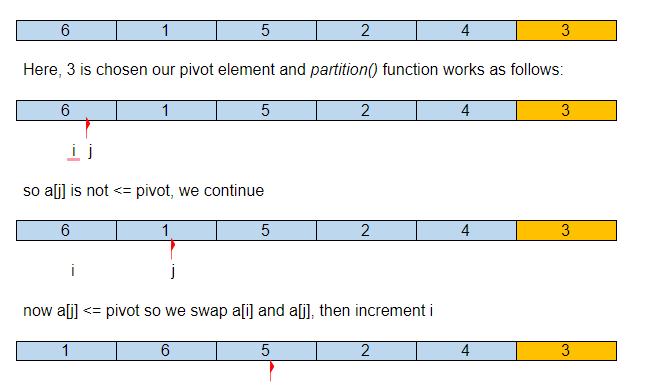

ดังนั้นหลังจากพาร์ติชันแรกของเรา องค์ประกอบ pivot จะอยู่ที่ตำแหน่งที่ถูกต้องในอาร์เรย์ที่จัดเรียง โดยองค์ประกอบที่เล็กกว่าทั้งหมดอยู่ทางซ้ายและมากกว่าทางขวา
ตอนนี้ QuickSort() จะถูกเรียกซ้ำสำหรับอาร์เรย์ย่อย {1,2} และ {6,4,5} และดำเนินการต่อจนกว่าอาร์เรย์จะถูกจัดเรียง
ต้องอ่าน: ประเภทของอัลกอริทึม AI ที่คุณควรรู้
การวิเคราะห์ความซับซ้อน
Ω ความซับซ้อนของเวลาเคสที่ดีที่สุด: Ω Θ ความซับซ้อนของเวลาเฉลี่ย: Θ O(n ความซับซ้อนของเวลากรณีที่แย่ที่สุด: O(n หากการแบ่งพาร์ติชันนำไปสู่อาร์เรย์ย่อยที่เกือบเท่ากัน เวลาทำงานจะดีที่สุด โดยมีความซับซ้อนของเวลาเป็น O(n*log n)

กรณีที่เลวร้ายที่สุดเกิดขึ้นกับอาร์เรย์ที่มีกรณีที่องค์ประกอบได้รับการจัดเรียงแล้ว และเลือก pivot เป็นองค์ประกอบสุดท้าย ในที่นี้ การแบ่งพาร์ติชั่นจะให้อาร์เรย์ย่อยที่ไม่สมดุล โดยที่องค์ประกอบทั้งหมดมีขนาดเล็กกว่าเดือยอยู่แล้ว และด้วยเหตุนี้จึงอยู่ทางด้านซ้าย และไม่มีองค์ประกอบทางด้านขวา
O(n*log n) O(n*log n)
บทสรุป
Quicksort เป็น อัลกอริทึมที่ ใช้ การเปรียบเทียบ และไม่ เสถียร การปรับให้เหมาะสมเล็กน้อยที่สามารถทำได้ คือการเรียกใช้ ฟังก์ชัน QuickSort() แบบเรียกซ้ำ สำหรับอาร์เรย์ย่อยที่เล็กกว่าก่อน จากนั้นจึงเรียกฟังก์ชันย่อยที่ใหญ่กว่า
โดยรวมแล้ว Quick Sort เป็นเทคนิคการเรียงลำดับที่มีประสิทธิภาพสูงซึ่งสามารถให้ประสิทธิภาพที่ดีกว่า Merge Sort ในกรณีของอาร์เรย์ที่มีขนาดเล็กกว่า
หากคุณสนใจที่จะเรียนรู้เพิ่มเติม ลองดูประกาศนียบัตร PG ของ upGrad & IIIT-B ในการเรียนรู้ของเครื่องและโปรแกรม AI
ข้อเสียของการใช้อัลกอริธึมแบบ Quicksort คืออะไร?
โดยทั่วไป อัลกอริธึมการเรียงลำดับอย่างรวดเร็วเป็นเทคนิคที่มีประสิทธิภาพและใช้กันอย่างแพร่หลายที่สุดสำหรับการจัดเรียงรายการขนาดใดก็ได้ แม้ว่าจะมีข้อเสียอยู่บ้าง เป็นวิธีการที่เปราะบาง ซึ่งหมายความว่าหากข้อบกพร่องเล็กๆ น้อยๆ ในการใช้งานไม่ได้ถูกตรวจสอบ ผลลัพธ์ก็จะได้รับผลกระทบไปด้วย การนำไปใช้งานทำได้ยาก โดยเฉพาะอย่างยิ่งหากไม่มีการเรียกซ้ำ ข้อจำกัดเล็กๆ น้อยๆ ประการหนึ่งของอัลกอริธึมการจัดเรียงอย่างรวดเร็วคือประสิทธิภาพในกรณีที่แย่ที่สุดนั้นเทียบได้กับการแสดงทั่วไปของบับเบิล การแทรก หรือการเลือกประเภท
อัลกอริธึมการเรียงลำดับที่ฝากข้อมูลใช้ทำอะไร
อัลกอริธึมการจัดเรียงแบบบัคเก็ตเป็นวิธีการเรียงลำดับที่ใช้ในการจัดองค์ประกอบต่างๆ ลงในกลุ่มต่างๆ มีชื่อเรียกเช่นนี้เนื่องจากกลุ่มย่อยต่างๆ ถูกเรียกว่าบัคเก็ต เนื่องจากการกระจายองค์ประกอบที่สม่ำเสมอจึงทำให้มีความรวดเร็วแบบไม่แสดงอาการ อย่างไรก็ตาม หากเรามีอาร์เรย์ขนาดใหญ่ จะไม่ได้ผลเนื่องจากจะเพิ่มต้นทุนของกระบวนการทั้งหมด ทำให้มีราคาไม่แพง
อันไหนดีกว่าที่จะใช้— Quicksort หรือ mergesort Algorithm?
สำหรับชุดข้อมูลขนาดเล็ก Quicksort จะเร็วกว่าอัลกอริธึมการจัดเรียงอื่นๆ เช่น Selection Sort แต่ Mergesort มีประสิทธิภาพที่สม่ำเสมอโดยไม่คำนึงถึงขนาดข้อมูล ในทางกลับกัน Quicksort จะมีประสิทธิภาพน้อยกว่าการรวมเมื่อจัดการกับอาร์เรย์ที่ใหญ่กว่า Mergesort ใช้พื้นที่มากกว่า แต่ Quicksort ใช้พื้นที่เพียงเล็กน้อย โดยเฉพาะอย่างยิ่ง Quicksort มีตำแหน่งแคชที่แข็งแกร่ง ทำให้เร็วกว่าการรวมการเรียงลำดับในหลาย ๆ สถานการณ์ เช่น ในสภาพแวดล้อมหน่วยความจำเสมือน ผลลัพธ์ที่ได้คือ Quicksort มีประสิทธิภาพเหนือกว่าอัลกอริทึมการผสานรวม
