快速排序算法解释[示例]

快速排序基于分治算法的概念，这也是合并排序中使用的概念。 不同之处在于，在快速排序中，最重要或最重要的工作是在将数组分区（或划分）为子数组时完成的，而在合并排序的情况下，所有主要工作都发生在合并子数组期间。 对于快速排序，合并步骤无关紧要。

快速排序也称为分区交换排序。 该算法将给定的数字数组分为三个主要部分：

1. 小于枢轴元素的元素
2. 枢轴元素
3. 大于枢轴元素的元素

可以通过多种不同方式从给定的数字中选择枢轴元素：

1. 选择第一个元素
2. 选择最后一个元素（显示示例）
3. 选择任何随机元素
4. 选择中位数

例如：在数组{51, 36, 62, 13, 16, 7, 5, 24}中，我们将24作为枢轴（最后一个元素）。 所以在第一遍之后，列表会变成这样。

{5 7 16 13 24 62 36 51}

因此，在第一次遍历之后，对数组进行排序，使得小于所选枢轴的所有元素都位于其左侧，而所有大于所选枢轴的元素位于其右侧。 枢轴最终位于它应该在数组的排序版本中的位置。 现在子数组{5 7 16 13}和{62 36 51}被视为两个独立的数组，并且将对其应用相同的递归逻辑，并且我们将继续这样做，直到对整个数组进行排序。

另请阅读：数据结构中的堆排序

它是如何工作的？

这些是快速排序算法中遵循的步骤：

1. 我们选择我们的枢轴作为最后一个元素，并且我们第一次开始对数组进行分区（或划分）。
2. 在这个分区算法中，数组被分成 2 个子数组，这样所有小于枢轴的元素都将位于枢轴的左侧，而所有大于枢轴的元素将位于其右侧。
3. 并且枢轴元素将处于其最终排序位置。
4. 左右子数组中的元素不必排序。
5. 然后我们递归地选择左右子数组，并通过在子数组中选择一个枢轴对它们中的每一个执行分区，并重复这些步骤。

下面显示了该算法在 C++ 代码中的工作方式，使用示例数组。

void QuickSort(int a[], int low, int high)

{

如果（高<低）

返回;

int p=分区（a，低，高）；

快速排序(a,low,p-1);

快速排序(a,p+1,high);

}

int 分区（int a[]，int 低，int 高）

{

诠释枢轴=一个[高]；

诠释我=低；

for(int j=low;j<high;j++)

{

if(a[j]<=pivot)

{

交换(&a[j],&a[i]);

我++；

}

}

交换(&a[i],&a[high]);

返回我；

}

主函数（）

{

int arr[]={6,1,5,2,4,3};

快速排序（arr,0,5）；

cout<<"排序后的数组为：";

for(int i=0; i<6; i++)

cout<<arr[i]<<" ";

返回0；

}

下面是快速排序如何对给定数组进行排序的图示。

假设初始输入数组是：

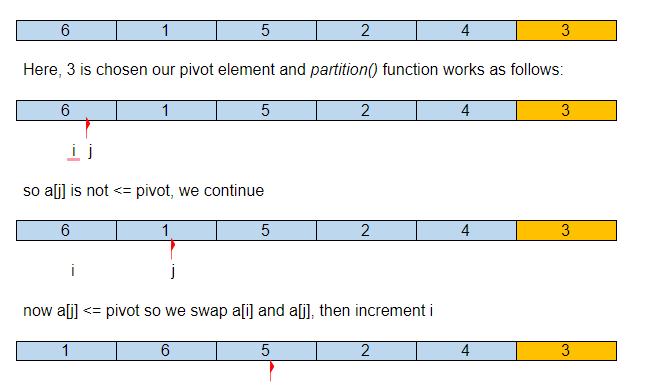
因此，在我们的第一个分区之后，枢轴元素在排序数组中的正确位置，其所有较小的元素在左侧，较大的元素在右侧。

现在QuickSort()将递归调用子数组 {1,2} 和 {6,4,5} 并继续直到数组排序。

必读：你应该知道的人工智能算法类型

复杂性分析

Ω 最佳案例时间复杂度： Ω Θ 平均时间复杂度： Θ O(n 最坏情况时间复杂度： O(n 如果分区导致几乎相等的子数组，那么运行时间是最好的，时间复杂度为 O(n*log n)。

最坏的情况发生在元素已经排序的数组中，并且选择枢轴作为最后一个元素。 在这里，分区给出了不平衡的子数组，其中所有元素都已经小于枢轴，因此在其左侧，而右侧没有元素。

O(n*log n)O(n*log n)

结论

快速排序是一种基于比较的算法，它并不稳定。 可以进行的一个小优化是先为较小的子数组调用递归QuickSort()函数，然后再为较大的子数组调用。

总体而言，快速排序是一种高效的排序技术，在较小数组的情况下可以提供比合并排序更好的性能。

如果您热衷于了解更多信息，请查看 upGrad 和 IIIT-B 的机器学习和 AI 计划的 PG 文凭。