Объяснение алгоритма быстрой сортировки [с примером]

Быстрая сортировка основана на концепции алгоритма « разделяй и властвуй », которая также используется в сортировке слиянием. Разница в том, что при быстрой сортировке самая важная или значительная работа выполняется при разбиении (или делении) массива на подмассивы, а при сортировке слиянием вся основная работа выполняется при объединении подмассивов. Для быстрой сортировки шаг объединения незначителен.

Быстрая сортировка также называется сортировкой с обменом разделами . Этот алгоритм делит заданный массив чисел на три основные части:

1. Элементы меньше, чем опорный элемент
2. Поворотный элемент
3. Элементы больше, чем опорный элемент

Элемент Pivot можно выбрать из заданных чисел разными способами:

1. Выбор первого элемента
2. Выбор последнего элемента (показан пример)
3. Выбор любого случайного элемента
4. Выбор медианы

Например: в массиве {51, 36, 62, 13, 16, 7, 5, 24} мы берем 24 в качестве точки опоры (последний элемент). Таким образом, после первого прохода список будет изменен следующим образом.

{5 7 16 13 24 62 36 51}

Следовательно, после первого прохода массив сортируется таким образом, что все элементы, меньшие выбранной опорной точки, находятся на его левой стороне, а все большие элементы — на правой. Наконец, точка поворота находится в той позиции, в которой она должна находиться в отсортированной версии массива. Теперь подмассивы {5 7 16 13} и {62 36 51} рассматриваются как два отдельных массива, и к ним будет применяться одна и та же рекурсивная логика, и мы будем продолжать делать это до тех пор, пока весь массив не будет отсортирован.

Читайте также: Сортировка кучей в структуре данных

Как это работает?

Вот шаги, выполняемые в алгоритме быстрой сортировки:

1. Мы выбираем наш стержень в качестве последнего элемента и начинаем разбивать (или делить) массив в первый раз.
2. В этом алгоритме разбиения массив разбивается на 2 подмассива таким образом, что все элементы, меньшие, чем опорная точка, будут находиться на левой стороне опорной точки, а все элементы, превышающие опорную, будут находиться на правой стороне от нее.
3. И поворотный элемент будет в своей конечной отсортированной позиции.
4. Элементы в левом и правом подмассивах не нужно сортировать.
5. Затем мы рекурсивно выбираем левый и правый подмассивы и выполняем разбиение каждого из них, выбирая точку опоры в подмассивах, и шаги повторяются для одного и того же.

Ниже показано, как алгоритм работает в коде C++ с использованием примера массива.

void QuickSort (int a [], int low, int high)

{

если (высокий<низкий)

вернуть;

int p = раздел (а, низкий, высокий);

Быстрая сортировка (а, низкий, p-1);

Быстрая сортировка (а, р+1, высокий);

}

раздел int (int a [], int low, int high)

{

INT Pivot=a[высокий];

интервал я = низкий;

for(int j=низкий; j<высокий; j++)

{

если(a[j]<=поворот)

{

своп(&a[j],&a[i]);

я++;

}

}

своп(&a[i],&a[высокий]);

вернуть я;

}

основной ()

{

интервал обр[]={6,1,5,2,4,3};

Быстрая сортировка (обр, 0,5);

cout<<"Отсортированный массив: ";

для (целое я = 0; я <6; я ++)

cout<<arr[i]<<” “;

вернуть 0;

}

Ниже показано графическое представление того, как быстрая сортировка будет сортировать данный массив.

Предположим, что исходный входной массив:

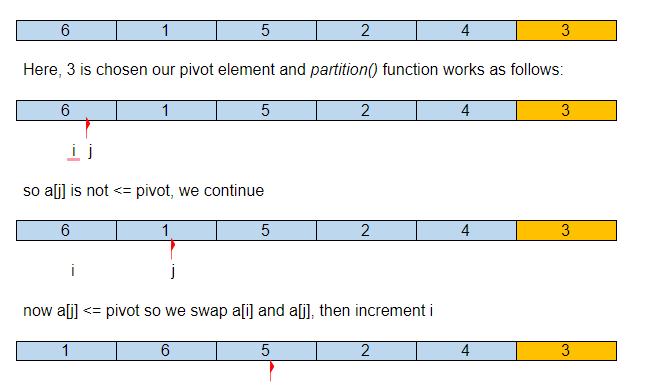
Таким образом, после нашего первого раздела опорный элемент находится на правильном месте в отсортированном массиве, со всеми его меньшими элементами слева и большими справа.

Теперь QuickSort() будет вызываться рекурсивно для подмассивов {1,2} и {6,4,5} и продолжаться до тех пор, пока массив не будет отсортирован.

Обязательно к прочтению: типы алгоритмов ИИ, которые вы должны знать

Анализ сложности

Ω Временная сложность в наилучшем случае: Ω Θ Средняя временная сложность: Θ O(n Временная сложность в наихудшем случае: O(n Если разбиение приводит к почти равным подмассивам, то время выполнения будет оптимальным, а временная сложность равна O(n*log n).

В худшем случае это случается с массивами, в которых элементы уже отсортированы, а сводная точка выбирается последним элементом. Здесь разбиение дает несбалансированные подмассивы, в которых все элементы уже меньше, чем точка опоры и, следовательно, находятся на ее левой стороне, а элементы на правой стороне отсутствуют.

O(n*log n) O (n * log n)

Заключение

Быстрая сортировка — это алгоритм, основанный на сравнении , и он нестабилен . Небольшая оптимизация, которую можно выполнить, заключается в вызове рекурсивной функции QuickSort() сначала для меньшего подмассива, а затем для большего подмассива.

В целом, быстрая сортировка — это высокоэффективный метод сортировки, который может обеспечить более высокую производительность, чем сортировка слиянием, в случае небольших массивов.

Если вы хотите узнать больше, ознакомьтесь с дипломом PG upGrad & IIIT-B по программе машинного обучения и искусственного интеллекта.