Spiegazione dell'algoritmo Quicksort [con esempio]

Quick Sort si basa sul concetto di algoritmo Divide and Conquer , che è anche il concetto utilizzato in Merge Sort. La differenza è che nell'ordinamento rapido il lavoro più importante o significativo viene svolto durante il partizionamento (o la divisione) dell'array in sottoarray, mentre in caso di ordinamento mediante unione, tutto il lavoro principale avviene durante l' unione dei sottoarray. Per l'ordinamento rapido, il passaggio di combinazione è insignificante.

Quick Sort è anche chiamato partition-exchange sort . Questo algoritmo divide la data matrice di numeri in tre parti principali:

1. Elementi inferiori all'elemento pivot
2. Elemento pivot
3. Elementi maggiori dell'elemento pivot

L'elemento pivot può essere scelto dai numeri indicati in molti modi diversi:

1. Scelta del primo elemento
2. Scelta dell'ultimo elemento (esempio mostrato)
3. Scegliere qualsiasi elemento casuale
4. Scelta della mediana

Ad esempio: nell'array {51, 36, 62, 13, 16, 7, 5, 24} , prendiamo 24 come pivot (ultimo elemento). Quindi, dopo il primo passaggio, l'elenco verrà modificato in questo modo.

{5 7 16 13 24 62 36 51}

Quindi, dopo il primo passaggio, l'array viene ordinato in modo tale che tutti gli elementi inferiori al pivot scelto siano sul lato sinistro e tutti gli elementi maggiori sul lato destro. Il pivot è finalmente nella posizione in cui dovrebbe trovarsi nella versione ordinata dell'array. Ora i sottoarray {5 7 16 13} e {62 36 51} sono considerati come due array separati e su di essi verrà applicata la stessa logica ricorsiva e continueremo a farlo fino a quando l'array completo non sarà ordinato.

Leggi anche: Ordinamento dell'heap nella struttura dei dati

Come funziona?

Questi sono i passaggi seguiti nell'algoritmo di ordinamento rapido:

1. Scegliamo il nostro pivot come ultimo elemento e iniziamo a partizionare (o dividere) l'array per la prima volta.
2. In questo algoritmo di partizionamento, l'array è suddiviso in 2 sottoarray in modo tale che tutti gli elementi più piccoli del pivot si trovino sul lato sinistro del pivot e tutti gli elementi maggiori del pivot si trovino sul lato destro di esso.
3. E l'elemento pivot sarà nella sua posizione ordinata finale.
4. Gli elementi nei sottoarray sinistro e destro non devono essere ordinati.
5. Quindi selezioniamo ricorsivamente i sottoarray sinistro e destro ed eseguiamo il partizionamento su ciascuno di essi scegliendo un pivot nei sottoarray e i passaggi vengono ripetuti per lo stesso.

Di seguito è mostrato come funziona l'algoritmo nel codice C++, usando un array di esempio.

void QuickSort(int a[], int low, int high)

{

se(alto<basso)

Restituzione;

int p= partizione(a,basso,alto);

QuickSort(a,basso,p-1);

QuickSort(a,p+1,alto);

}

int partition(int a[], int low, int high)

{

int pivot=a[alto];

int i=basso;

for(int j=basso; j<alto; j++)

{

if(a[j]<=pivot)

{

scambia(&a[j],&a[i]);

i++;

}

}

swap(&a[i],&a[alto]);

ritorno io;

}

int principale()

{

int arr[]={6,1,5,2,4,3};

Ordinamento rapido(arr,0,5);

cout<<”L'array ordinato è: “;

for(int i=0; i<6; i++)

cout<<arr[i]<<” “;

restituire 0;

}

Di seguito è riportata una rappresentazione grafica di quanto velocemente l'ordinamento ordinerà l'array specificato.

Supponiamo che l'array di input iniziale sia:

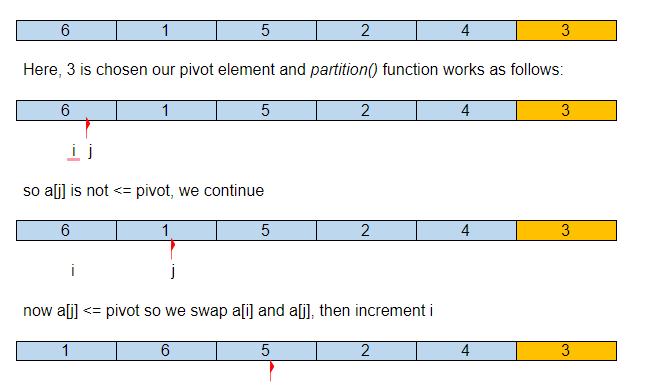
Quindi, dopo la nostra prima partizione, l'elemento pivot si trova nella posizione corretta nell'array ordinato, con tutti i suoi elementi più piccoli a sinistra e maggiori a destra.

Ora QuickSort() verrà chiamato ricorsivamente per i sottoarray {1,2} e {6,4,5} e continuerà fino a quando l'array non sarà ordinato.

Da leggere: Tipi di algoritmi di intelligenza artificiale che dovresti conoscere

Analisi della complessità

Ω Complessità temporale del caso migliore: Ω Θ Complessità temporale media: Θ O(n Complessità temporale del caso peggiore: O(n Se il partizionamento porta a sottoarray quasi uguali, il tempo di esecuzione è il migliore, con una complessità temporale pari a O(n*log n).

Il caso peggiore si verifica per gli array con casi in cui gli elementi sono già ordinati e il pivot viene scelto come ultimo elemento. Qui la partizione dà sottoarray sbilanciati, dove tutti gli elementi sono già più piccoli del pivot e quindi sul suo lato sinistro, e nessun elemento sul lato destro.

O(n*log n) O(n*log n)

Conclusione

Quicksort è un algoritmo basato sul confronto e non è stabile . Una piccola ottimizzazione che può essere eseguita consiste nel chiamare prima la funzione ricorsiva QuickSort() per il sottoarray più piccolo e poi per il sottoarray più grande.

Nel complesso, Quick Sort è una tecnica di ordinamento altamente efficiente che può fornire prestazioni migliori rispetto a Merge Sort nel caso di array più piccoli.

Se sei interessato a saperne di più, dai un'occhiata al diploma PG di upGrad e IIIT-B in Machine Learning e programma AI.