Penjelasan Algoritma Quicksort [Dengan Contoh]

Quick Sort didasarkan pada konsep algoritma Divide and Conquer , yang juga merupakan konsep yang digunakan dalam Merge Sort. Perbedaannya adalah, dalam quick sort pekerjaan yang paling penting atau signifikan dilakukan saat mempartisi (atau membagi) array menjadi subarray, sedangkan dalam kasus merge sort, semua pekerjaan utama terjadi selama penggabungan subarray. Untuk quick sort, langkah menggabungkan tidak signifikan.

Quick Sort disebut juga sebagai partisi-tukar sort . Algoritma ini membagi array angka yang diberikan menjadi tiga bagian utama:

1. Elemen kurang dari elemen pivot
2. Elemen poros
3. Elemen yang lebih besar dari elemen pivot

Elemen pivot dapat dipilih dari angka yang diberikan dengan berbagai cara:

1. Memilih elemen pertama
2. Memilih elemen terakhir (contoh ditunjukkan)
3. Memilih elemen acak apa pun
4. Memilih median

Sebagai contoh: Dalam array {51, 36, 62, 13, 16, 7, 5, 24} , kami mengambil 24 sebagai pivot (elemen terakhir). Jadi setelah pass pertama, daftarnya akan berubah seperti ini.

{5 7 16 13 24 62 36 51}

Oleh karena itu setelah lintasan pertama, array diurutkan sedemikian rupa sehingga semua elemen yang kurang dari pivot yang dipilih berada di sisi kirinya dan semua elemen yang lebih besar di sisi kanannya. Pivot akhirnya berada pada posisi yang seharusnya dalam versi array yang diurutkan. Sekarang subarray {5 7 16 13} dan {62 36 51} dianggap sebagai dua larik terpisah, dan logika rekursif yang sama akan diterapkan pada mereka, dan kami akan terus melakukan ini sampai larik lengkap diurutkan.

Baca Juga: Heap Sortir dalam Struktur Data

Bagaimana cara kerjanya?

Ini adalah langkah-langkah yang diikuti dalam algoritma pengurutan cepat:

1. Kami memilih pivot kami sebagai elemen terakhir, dan kami mulai mempartisi (atau membagi) array untuk pertama kalinya.
2. Dalam algoritma partisi ini, array dipecah menjadi 2 subarray sehingga semua elemen yang lebih kecil dari pivot akan berada di sisi kiri pivot dan semua elemen yang lebih besar dari pivot akan berada di sisi kanannya.
3. Dan elemen pivot akan berada pada posisi terakhir yang diurutkan.
4. Elemen-elemen di subarray kiri dan kanan tidak harus diurutkan.
5. Kemudian kami secara rekursif memilih subarray kiri dan kanan, dan kami melakukan partisi pada masing-masing subarray dengan memilih pivot di subarray dan langkah-langkahnya diulang untuk hal yang sama.

Ditampilkan di bawah ini adalah cara kerja algoritma dalam kode C++, menggunakan contoh array.

void QuickSort(int a[], int rendah, int tinggi)

{

jika (tinggi < rendah)

kembali;

int p= partisi(a,rendah,tinggi);

QuickSort(a,rendah,p-1);

Sortir Cepat(a,p+1,tinggi);

}

int partisi(int a[], int rendah, int tinggi)

{

int pivot=a[tinggi];

int i=rendah;

untuk(int j=rendah; j<tinggi; j++)

{

jika(a[j]<=poros)

{

swap(&a[j],&a[i]);

saya++;

}

}

swap(&a[i],&a[tinggi]);

kembali saya;

}

int utama()

{

int arr[]={6,1,5,2,4,3};

Sortir Cepat(arr,0,5);

cout<<”Array yang diurutkan adalah: “;

untuk(int i=0; i<6; i++)

cout<<arr[i]<<” “;

kembali 0;

}

Di bawah ini adalah representasi bergambar tentang bagaimana quick sort akan mengurutkan array yang diberikan.

Misalkan array input awal adalah:

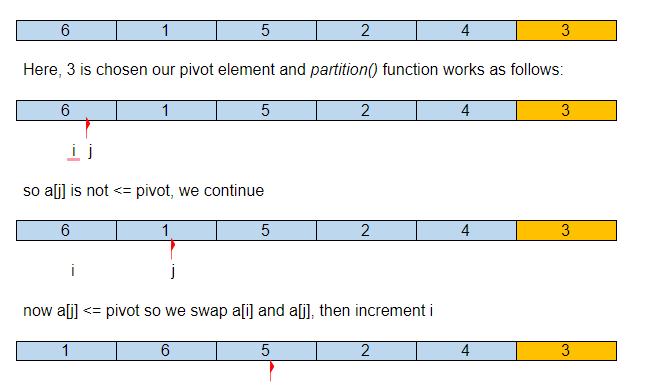
Jadi setelah partisi pertama kami, elemen pivot berada di tempat yang benar dalam array yang diurutkan, dengan semua elemen yang lebih kecil ke kiri dan lebih besar ke kanan.

Sekarang QuickSort() akan dipanggil secara rekursif untuk subarray {1,2} dan {6,4,5} dan terus berlanjut hingga array diurutkan.

Wajib Dibaca: Jenis-Jenis Algoritme AI Yang Harus Anda Ketahui

Analisis Kompleksitas

Ω Kompleksitas Waktu Kasus Terbaik: ( n Θ Kompleksitas Waktu Rata-rata: ( n O(n Kompleksitas Waktu Kasus Terburuk: O(n Jika partisi mengarah ke subarray yang hampir sama, maka waktu berjalan adalah yang terbaik, dengan kompleksitas waktu sebagai O(n*log n).

Kasus terburuk terjadi untuk array dengan kasus di mana elemen sudah diurutkan, dan pivot dipilih sebagai elemen terakhir. Di sini partisi memberikan subarray yang tidak seimbang, di mana semua elemen sudah lebih kecil dari pivot dan karenanya di sisi kirinya, dan tidak ada elemen di sisi kanan.

O(n*log n) O(n*log n)

Kesimpulan

Quicksort adalah algoritma berbasis perbandingan dan tidak stabil . Sebuah optimasi kecil yang dapat dilakukan, adalah dengan memanggil fungsi QuickSort() rekursif untuk subarray yang lebih kecil terlebih dahulu dan kemudian subarray yang lebih besar.

Secara keseluruhan, Quick Sort adalah teknik pengurutan yang sangat efisien yang dapat memberikan kinerja yang lebih baik daripada Merge Sort dalam kasus array yang lebih kecil.

Jika Anda tertarik untuk belajar lebih banyak, lihat Program PG Diploma dan Pembelajaran Mesin dan Program AI dari Grad & IIIT-B.