Quicksort-Algorithmus erklärt [mit Beispiel]

Quick Sort basiert auf dem Konzept des Divide-and-Conquer- Algorithmus, der auch bei Merge Sort verwendet wird. Der Unterschied besteht darin, dass beim schnellen Sortieren die wichtigste oder bedeutendste Arbeit beim Partitionieren (oder Teilen) des Arrays in Unterarrays ausgeführt wird, während beim Zusammenführen von Sortieren die gesamte Hauptarbeit beim Zusammenführen der Unterarrays erfolgt. Für eine schnelle Sortierung ist der Kombinationsschritt unbedeutend.

Quick Sort wird auch Partition-Exchange-Sortierung genannt . Dieser Algorithmus teilt das gegebene Array von Zahlen in drei Hauptteile:

1. Elemente kleiner als das Pivot-Element
2. Pivot-Element
3. Elemente größer als das Pivot-Element

Das Pivot-Element kann auf viele verschiedene Arten aus den angegebenen Nummern ausgewählt werden:

1. Auswahl des ersten Elements
2. Auswahl des letzten Elements (Beispiel gezeigt)
3. Auswahl eines zufälligen Elements
4. Wahl des Medians

Zum Beispiel: Im Array {51, 36, 62, 13, 16, 7, 5, 24} nehmen wir 24 als Pivot (letztes Element). Nach dem ersten Durchgang wird die Liste also wie folgt geändert.

{5 7 16 13 24 62 36 51}

Daher wird das Array nach dem ersten Durchlauf so sortiert, dass alle Elemente kleiner als der gewählte Drehpunkt auf seiner linken Seite und alle größeren Elemente auf seiner rechten Seite sind. Der Pivot befindet sich schließlich an der Position, an der er in der sortierten Version des Arrays sein sollte. Jetzt werden die Subarrays {5 7 16 13} und {62 36 51} als zwei separate Arrays betrachtet, und dieselbe rekursive Logik wird auf sie angewendet, und wir werden dies so lange tun, bis das vollständige Array sortiert ist.

Lesen Sie auch: Heap-Sortierung in der Datenstruktur

Wie funktioniert es?

Dies sind die Schritte, die im Schnellsortierungsalgorithmus ausgeführt werden:

1. Wir wählen unseren Pivot als letztes Element und beginnen damit, das Array zum ersten Mal zu partitionieren (oder zu teilen).
2. Bei diesem Partitionierungsalgorithmus wird das Array in 2 Subarrays aufgeteilt, sodass alle Elemente, die kleiner als der Pivot sind, auf der linken Seite des Pivots und alle Elemente, die größer als der Pivot sind, auf der rechten Seite davon liegen.
3. Und das Pivot-Element befindet sich an seiner endgültigen sortierten Position.
4. Die Elemente in den linken und rechten Subarrays müssen nicht sortiert werden.
5. Dann wählen wir rekursiv die linken und rechten Subarrays aus, und wir führen eine Partitionierung an jedem von ihnen durch, indem wir einen Drehpunkt in den Subarrays auswählen, und die Schritte werden für dieselben wiederholt.

Unten wird anhand eines Beispielarrays gezeigt, wie der Algorithmus in C++-Code funktioniert.

void QuickSort(int a[], int niedrig, int hoch)

{

wenn (hoch<niedrig)

Rückkehr;

int p= partition(a,low,high);

QuickSort(a,low,p-1);

QuickSort(a,p+1,hoch);

}

int partition(int a[], int niedrig, int hoch)

{

int Pivot = a [hoch];

int i=niedrig;

for(int j=low; j<high; j++)

{

if(a[j]<=Drehpunkt)

{

tauschen(&a[j],&a[i]);

i++;

}

}

swap(&a[i],&a[hoch]);

gib ich zurück;

}

int Haupt()

{

int arr[]={6,1,5,2,4,3};

QuickSort(arr,0,5);

cout<<”Das sortierte Array ist: “;

for(int i=0; i<6; i++)

cout<<arr[i]<<” “;

0 zurückgeben;

}

Unten sehen Sie eine bildliche Darstellung, wie die schnelle Sortierung das angegebene Array sortiert.

Angenommen, das anfängliche Eingabearray ist:

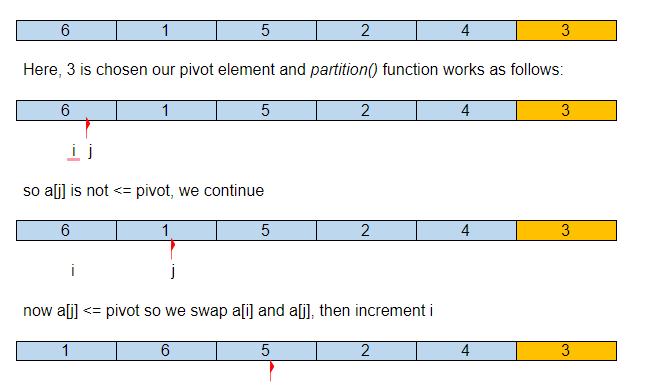
Nach unserer ersten Partition befindet sich das Pivot-Element also an der richtigen Stelle im sortierten Array, mit all seinen kleineren Elementen links und den größeren rechts.

Jetzt wird QuickSort() rekursiv für die Subarrays {1,2} und {6,4,5} aufgerufen und fortgesetzt, bis das Array sortiert ist.

Muss gelesen werden: Arten von KI-Algorithmen, die Sie kennen sollten

Komplexitätsanalyse

Ω Zeitkomplexität im besten Fall: Ω Θ Durchschnittliche Zeitkomplexität: Θ O(n Worst-Case-Zeitkomplexität: O(n Wenn die Partitionierung zu nahezu gleichen Subarrays führt, ist die Laufzeit am besten, mit einer Zeitkomplexität von O(n*log n).

Der schlimmste Fall tritt bei Arrays mit Fällen auf, in denen die Elemente bereits sortiert sind und Pivot als letztes Element ausgewählt wird. Hier ergibt die Partitionierung unausgeglichene Subarrays, bei denen alle Elemente bereits kleiner als der Pivot und damit auf dessen linker Seite sind, und keine Elemente auf der rechten Seite.

O(n*log n) O(n*log n)

Fazit

Quicksort ist ein vergleichsbasierter Algorithmus und nicht stabil . Eine kleine Optimierung, die durchgeführt werden kann, besteht darin, die rekursive QuickSort()- Funktion zuerst für das kleinere Subarray und dann für das größere Subarray aufzurufen.

Insgesamt ist Quick Sort eine hocheffiziente Sortiertechnik, die bei kleineren Arrays eine bessere Leistung als Merge Sort erzielen kann.

Wenn Sie mehr erfahren möchten, sehen Sie sich das PG-Diploma in maschinellem Lernen und KI-Programm von upGrad & IIIT-B an.