Algoritmo Quicksort explicado [con ejemplo]

Quick Sort se basa en el concepto del algoritmo Divide and Conquer , que también es el concepto utilizado en Merge Sort. La diferencia es que en la ordenación rápida, el trabajo más importante o significativo se realiza al particionar (o dividir) la matriz en subarreglos, mientras que en el caso de la ordenación por combinación, todo el trabajo principal ocurre durante la combinación de los subarreglos. Para la ordenación rápida, el paso de combinación es insignificante.

Quick Sort también se denomina clasificación de intercambio de partición . Este algoritmo divide la matriz dada de números en tres partes principales:

1. Elementos menores que el elemento pivote
2. Elemento de pivote
3. Elementos mayores que el elemento pivote

El elemento de pivote se puede elegir de los números dados de muchas maneras diferentes:

1. Elegir el primer elemento
2. Elegir el último elemento (ejemplo mostrado)
3. Elegir cualquier elemento aleatorio
4. Elegir la mediana

Por ejemplo: en el arreglo {51, 36, 62, 13, 16, 7, 5, 24} , tomamos 24 como pivote (último elemento). Entonces, después del primer pase, la lista se cambiará así.

{5 7 16 13 24 62 36 51}

Por lo tanto, después del primer paso, la matriz se ordena de manera que todos los elementos menores que el pivote elegido estén en su lado izquierdo y todos los elementos mayores en su lado derecho. El pivote finalmente está en la posición que se supone que debe estar en la versión ordenada de la matriz. Ahora los subarreglos {5 7 16 13} y {62 36 51} se consideran como dos arreglos separados, y se les aplicará la misma lógica recursiva, y seguiremos haciéndolo hasta que se ordene el arreglo completo.

Lea también: Heap Sort en la estructura de datos

¿Como funciona?

Estos son los pasos seguidos en el algoritmo de clasificación rápida:

1. Elegimos nuestro pivote como el último elemento y comenzamos a particionar (o dividir) la matriz por primera vez.
2. En este algoritmo de partición, la matriz se divide en 2 subarreglos, de modo que todos los elementos más pequeños que el pivote estarán en el lado izquierdo del pivote y todos los elementos más grandes que el pivote estarán en el lado derecho.
3. Y el elemento pivote estará en su posición ordenada final.
4. No es necesario ordenar los elementos de los subarreglos izquierdo y derecho.
5. Luego seleccionamos recursivamente los subarreglos izquierdo y derecho, y realizamos la partición en cada uno de ellos eligiendo un pivote en los subarreglos y los pasos se repiten para el mismo.

A continuación se muestra cómo funciona el algoritmo en código C++, utilizando una matriz de ejemplo.

void QuickSort(int a[], int low, int high)

{

si (alto <bajo)

regreso;

int p= partición(a,bajo,alto);

QuickSort(a,bajo,p-1);

QuickSort(a,p+1,alto);

}

int partición(int a[], int bajo, int alto)

{

int pivote=a[alto];

int i=bajo;

for(int j=bajo; j<alto; j++)

{

si(a[j]<=pivote)

{

intercambiar(&a[j],&a[i]);

yo++;

}

}

swap(&a[i],&a[alto]);

devolver yo;

}

int principal()

{

matriz int[]={6,1,5,2,4,3};

Clasificación rápida (arr, 0,5);

cout<<”La matriz ordenada es: “;

para(int i=0; i<6; i++)

cout<<arr[i]<<” “;

devolver 0;

}

A continuación se muestra una representación pictórica de qué tan rápido ordenará la matriz dada.

Supongamos que la matriz de entrada inicial es:

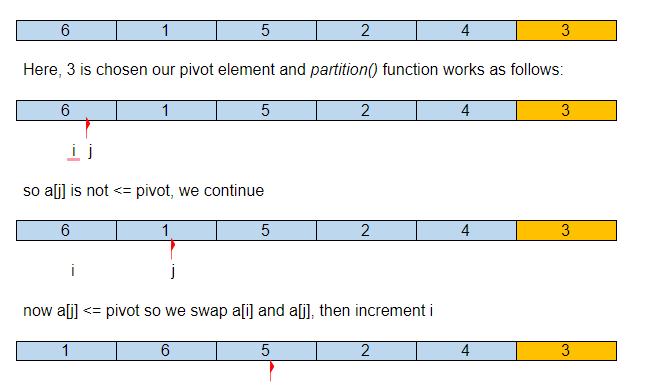
Entonces, después de nuestra primera partición, el elemento pivote está en su lugar correcto en la matriz ordenada, con todos sus elementos más pequeños a la izquierda y los más grandes a la derecha.

Ahora QuickSort() se llamará recursivamente para los subarreglos {1,2} y {6,4,5} y continuará hasta que se ordene el arreglo.

Debe leer: Tipos de algoritmos de IA que debe conocer

Análisis de Complejidad

Ω Complejidad de tiempo en el mejor de los casos: Ω Θ Complejidad de Tiempo Promedio: Θ O(n Complejidad temporal en el peor de los casos: O(n Si la partición conduce a subarreglos casi iguales, entonces el tiempo de ejecución es el mejor, con una complejidad de tiempo de O(n*log n).

El peor de los casos ocurre con las matrices en las que los elementos ya están ordenados y se elige el pivote como el último elemento. Aquí la partición da subarreglos desequilibrados, donde todos los elementos ya son más pequeños que el pivote y, por lo tanto, en su lado izquierdo, y ningún elemento en el lado derecho.

O(n*log n) O (n * log n)

Conclusión

Quicksort es un algoritmo basado en la comparación y no es estable . Una pequeña optimización que se puede hacer es llamar a la función recursiva QuickSort() para el subarreglo más pequeño primero y luego para el subarreglo más grande.

En general, Quick Sort es una técnica de clasificación altamente eficiente que puede brindar un mejor rendimiento que Merge Sort en el caso de arreglos más pequeños.

Si está interesado en aprender más, consulte el Diploma PG en aprendizaje automático e inteligencia artificial de upGrad & IIIT-B.