شرح خوارزمية Quicksort [مع مثال]

يعتمد التصنيف السريع على مفهوم خوارزمية التقسيم والقهر ، وهو أيضًا المفهوم المستخدم في دمج الفرز. الفرق هو أنه في الفرز السريع ، يتم تنفيذ العمل الأكثر أهمية أو أهمية أثناء تقسيم (أو تقسيم) المصفوفة إلى مصفوفات فرعية ، بينما في حالة فرز الدمج ، تحدث جميع الأعمال الرئيسية أثناء دمج المصفوفات الفرعية. للفرز السريع ، تكون خطوة الدمج غير مهمة.

يُطلق على "الفرز السريع" أيضًا "فرز تبادل الأقسام" . تقسم هذه الخوارزمية مجموعة الأرقام المحددة إلى ثلاثة أجزاء رئيسية:

1. العناصر الأقل من العنصر المحوري
2. عنصر محوري
3. العناصر الأكبر من العنصر المحوري

يمكن اختيار العنصر المحوري من الأرقام المحددة بعدة طرق مختلفة:

1. اختيار العنصر الأول
2. اختيار العنصر الأخير (المثال موضح)
3. اختيار أي عنصر عشوائي
4. اختيار الوسيط

على سبيل المثال: في المصفوفة {51 ، 36 ، 62 ، 13 ، 16 ، 7 ، 5 ، 24} ، نأخذ 24 كمحور ( العنصر الأخير). لذلك بعد المرور الأول ، سيتم تغيير القائمة على هذا النحو.

{5 7 16 13 24 62 36 51}

ومن ثم بعد المرور الأول ، يتم فرز المصفوفة بحيث تكون جميع العناصر الأقل من المحور المختار على جانبها الأيسر وجميع العناصر الأكبر على جانبها الأيمن. أصبح المحور أخيرًا في الموضع المفترض أن يكون في النسخة المصنفة من المصفوفة. الآن يتم اعتبار المصفوفتين الفرعيتين {5 7 16 13} و {62 36 51} كمصفوفتين منفصلتين ، وسيتم تطبيق نفس المنطق العودي عليهما ، وسنواصل القيام بذلك حتى يتم فرز المصفوفة بالكامل.

اقرأ أيضًا: فرز الكومة في بنية البيانات

كيف يعمل؟

هذه هي الخطوات المتبعة في خوارزمية الفرز السريع:

1. نختار المحور الخاص بنا كعنصر أخير ، ونبدأ في تقسيم (أو تقسيم) المصفوفة لأول مرة.
2. في خوارزمية التقسيم هذه ، يتم تقسيم المصفوفة إلى مصفوفتين فرعيتين بحيث تكون جميع العناصر الأصغر من المحور على الجانب الأيسر من المحور وستكون جميع العناصر الأكبر من المحور على الجانب الأيمن منه.
3. وسيكون العنصر المحوري في موضعه الفرز النهائي.
4. لا يلزم فرز العناصر الموجودة في المصفوفات الفرعية اليمنى واليسرى.
5. ثم نختار بشكل متكرر المصفوفتين الفرعيتين اليمنى واليسرى ، ونقوم بالتقسيم على كل منهما عن طريق اختيار محور في المصفوفتين الفرعيتين وتتكرر الخطوات لنفسه.

الموضح أدناه هو كيفية عمل الخوارزمية في كود C ++ ، باستخدام مثال مصفوفة.

QuickSort باطل (int a [] ، int low ، int high)

{

إذا (مرتفع <منخفض)

إرجاع؛

int p = قسم (a ، منخفض ، مرتفع) ؛

QuickSort (أ ، منخفض ، ف 1) ؛

QuickSort (أ ، ف + 1 ، مرتفع) ؛

}

قسم int (int a [] ، int low ، int high)

{

int pivot = a [مرتفع] ؛

int أنا = منخفض ؛

لـ (int j = منخفض ؛ j <مرتفع ؛ j ++)

{

إذا (a [j] <= محور)

{

مبادلة (& a [j]، & a [i]) ؛

أنا ++ ؛

}

}

مقايضة (& a [i]، & a [high]) ؛

العودة أنا

}

انت مين()

{

int arr [] = {6،1،5،2،4،3} ؛

QuickSort (الوصول ، 0.5) ؛

cout << "المصفوفة التي تم فرزها هي:"؛

لـ (int i = 0 ؛ i <6 ؛ i ++)

cout << arr [i] << ""؛

العودة 0 ؛

}

يوجد أدناه تمثيل تصويري لكيفية الفرز السريع للمصفوفة المحددة.

افترض أن صفيف الإدخال الأولي هو:

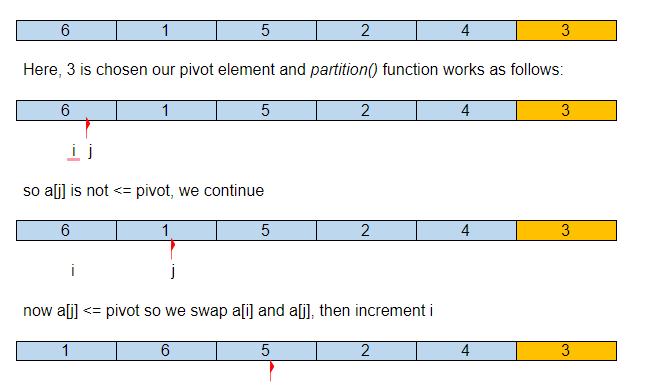
إذن ، بعد القسم الأول ، يكون العنصر المحوري في مكانه الصحيح في المصفوفة المصنفة ، مع كل عناصره الأصغر إلى اليسار وأكبر إلى اليمين.

الآن سيتم استدعاء QuickSort () بشكل متكرر للمصفوفات الفرعية {1،2} و {6،4،5} وسيستمر حتى يتم فرز المصفوفة.

يجب أن تقرأ: أنواع خوارزميات الذكاء الاصطناعي التي يجب أن تعرفها

تحليل التعقيد

Ω أفضل تعقيد لوقت الحالة: Ω Θ متوسط ​​تعقيد الوقت: Θ O(n صعوبة وقت الحالة الأسوأ: O (رقم إذا أدى التقسيم إلى مصفوفات فرعية متساوية تقريبًا ، فإن وقت التشغيل هو الأفضل ، مع تعقيد زمني مثل O (n * log n).

أسوأ حالة تحدث للمصفوفات ذات الحالات التي تم فيها فرز العناصر بالفعل ، ويتم اختيار المحور كعنصر أخير. هنا يعطي التقسيم مصفوفات فرعية غير متوازنة ، حيث تكون جميع العناصر بالفعل أصغر من المحور ومن ثم على جانبه الأيسر ، ولا توجد عناصر على الجانب الأيمن.

O(n*log n) O (n * log n)

خاتمة

Quicksort هي خوارزمية قائمة على المقارنة وهي غير مستقرة . التحسين الصغير الذي يمكن القيام به ، هو استدعاء دالة QuickSort () العودية للمصفوفة الفرعية الأصغر أولاً ثم المجموعة الفرعية الأكبر.

بشكل عام ، يعد الفرز السريع تقنية فرز عالية الكفاءة يمكنها تقديم أداء أفضل من دمج الفرز في حالة المصفوفات الأصغر.

إذا كنت حريصًا على تعلم المزيد ، فتحقق من دبلوم PG في برنامج التعلم الآلي والذكاء الاصطناعي من upGrad & IIIT-B.