Algoritmo Quicksort explicado [com exemplo]

O Quick Sort é baseado no conceito do algoritmo Divide and Conquer , que também é o conceito usado no Merge Sort. A diferença é que na ordenação rápida o trabalho mais importante ou significativo é feito ao particionar (ou dividir) o array em subarrays, enquanto no caso de merge sort, todo o trabalho principal acontece durante a fusão dos subarrays. Para classificação rápida, a etapa de combinação é insignificante.

O Quick Sort também é chamado de partition-exchange sort . Este algoritmo divide a matriz de números fornecida em três partes principais:

1. Elementos menores que o elemento pivô
2. Elemento de pivô
3. Elementos maiores que o elemento pivô

O elemento pivô pode ser escolhido a partir dos números fornecidos de muitas maneiras diferentes:

1. Escolhendo o primeiro elemento
2. Escolhendo o último elemento (exemplo mostrado)
3. Escolhendo qualquer elemento aleatório
4. Escolhendo a mediana

Por exemplo: No array {51, 36, 62, 13, 16, 7, 5, 24} , tomamos 24 como pivô (último elemento). Então, após a primeira passagem, a lista será alterada assim.

{5 7 16 13 24 62 36 51}

Portanto, após a primeira passagem, a matriz é classificada de modo que todos os elementos menores que o pivô escolhido estejam no lado esquerdo e todos os elementos maiores no lado direito. O pivô está finalmente na posição em que deveria estar na versão ordenada do array. Agora os subarrays {5 7 16 13} e {62 36 51} são considerados como dois arrays separados, e a mesma lógica recursiva será aplicada a eles, e continuaremos fazendo isso até que o array completo seja ordenado.

Leia também: Heap Sort na Estrutura de Dados

Como funciona?

Estas são as etapas seguidas no algoritmo de classificação rápida:

1. Escolhemos nosso pivô como o último elemento e começamos a particionar (ou dividir) o array pela primeira vez.
2. Neste algoritmo de particionamento, o array é dividido em 2 subarrays de tal forma que todos os elementos menores que o pivô estarão no lado esquerdo do pivô e todos os elementos maiores que o pivô estarão no lado direito dele.
3. E o elemento pivô estará em sua posição final classificada.
4. Os elementos nas submatrizes esquerda e direita não precisam ser classificados.
5. Em seguida, escolhemos recursivamente os subarranjos esquerdo e direito e executamos o particionamento em cada um deles escolhendo um pivô nos subarranjos e os passos são repetidos para o mesmo.

Abaixo é mostrado como o algoritmo funciona em código C++, usando um array de exemplo.

void QuickSort(int a[], int baixo, int alto)

{

if(alto<baixo)

Retorna;

int p= partição(a,baixo,alto);

QuickSort(a,baixo,p-1);

QuickSort(a,p+1,alta);

}

int partition(int a[], int low, int high)

{

int pivô=a[alto];

int i=baixo;

for(int j=baixo; j<alto; j++)

{

if(a[j]<=pivô)

{

swap(&a[j],&a[i]);

i++;

}

}

swap(&a[i],&a[alta]);

retorno eu;

}

int main()

{

int arr[]={6,1,5,2,4,3};

QuickSort(arr,0,5);

cout<<”O array ordenado é: “;

for(int i=0; i<6; i++)

cout<<arr[i]<<” “;

retornar 0;

}

Abaixo está uma representação pictórica de como a classificação rápida classificará a matriz fornecida.

Suponha que a matriz de entrada inicial seja:

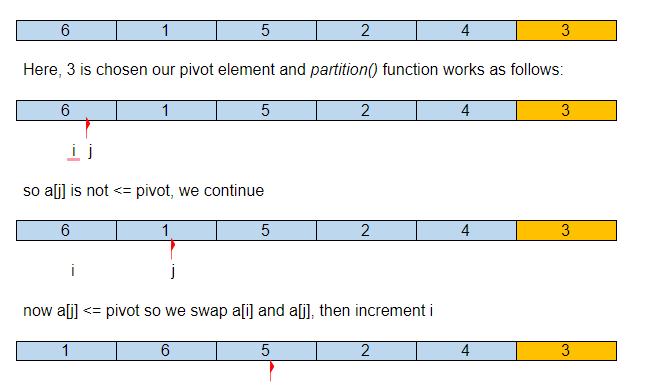
Então, após nossa primeira partição, o elemento pivô está em seu lugar correto no array ordenado, com todos os seus elementos menores à esquerda e maiores à direita.

Agora QuickSort() será chamado recursivamente para os subarrays {1,2} e {6,4,5} e continuará até que o array seja ordenado.

Deve ler: Tipos de algoritmos de IA que você deve conhecer

Análise de Complexidade

Ω Complexidade de tempo do melhor caso: Ω Θ Complexidade de tempo médio: Θ O(n Complexidade de tempo de pior caso: O(n Se o particionamento leva a subarrays quase iguais, então o tempo de execução é o melhor, com complexidade de tempo como O(n*log n).

O pior caso acontece para arrays com casos em que os elementos já estão ordenados e pivô é escolhido como o último elemento. Aqui o particionamento dá subarrays desbalanceados, onde todos os elementos já são menores que o pivô e, portanto, do lado esquerdo, e nenhum elemento do lado direito.

O(n*log n) O(n*log n)

Conclusão

Quicksort é um algoritmo baseado em comparação e não é estável . Uma pequena otimização que pode ser feita é chamar a função recursiva QuickSort() para o subarray menor primeiro e depois para o subarray maior.

No geral, o Quick Sort é uma técnica de classificação altamente eficiente que pode oferecer melhor desempenho do que o Merge Sort no caso de arrays menores.

Se você estiver interessado em aprender mais, confira o PG Diploma in Machine Learning and AI Program da upGrad & IIIT-B.