機器學習中的同方差性：檢測、影響和如何治療

在本教程結束時，您將了解以下內容：

• 什麼是同方差和異方差？
• 如何知道是否存在異方差。
• 機器學習中異方差的影響。
• 處理異方差。

什麼是同方差和異方差？

Homoscedasticity 意味著具有“相同的方差”。 在線性回歸中，主要假設之一是誤差或殘差項（Y_Pred – Y_actual）中存在同方差性。

換句話說，線性回歸假設對於所有實例，誤差項都是相同的並且方差很小。

讓我們藉助一個例子來理解它。 考慮我們有兩個變量——房子的地毯面積和房子的價格。 隨著地毯面積的增加，價格也隨之上漲。

因此，我們擬合了一個線性回歸模型，並看到誤差自始至終具有相同的方差。 下圖中的圖表 X 軸為地毯面積，Y 軸為價格。

如您所見，預測幾乎沿著線性回歸線，並且始終具有相似的方差。

此外，如果我們在 X 軸上繪製這些殘差，我們會看到它沿著平行於 X 軸的直線。 這是同方差性的明顯標誌

圖片來源

當違反這個條件時，意味著模型中存在異方差。 考慮與上述相同的示例，假設對於地毯面積較小的房屋，誤差或殘差或非常小。 並且隨著地毯面積的增加，預測的方差增加，這導致誤差或殘差項的值增加。 當我們再次繪製這些值時，我們會看到典型的圓錐曲線，這強烈表明模型中存在異方差。

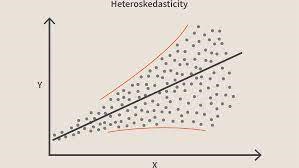
圖片來源具體來說，異方差是自變量範圍內殘差方差的系統性增加或減少。 這是一個問題，因為同方差性是線性回歸的假設，所有誤差都應該具有相同的方差。 了解有關線性回歸的更多信息

加入來自世界頂級大學的在線機器學習課程——碩士、高管研究生課程和 ML 和 AI 高級證書課程，以加快您的職業生涯。

如何知道是否存在異方差？

用最簡單的術語來說，了解是否存在異方差的最簡單方法是繪製殘差圖。 如果您看到存在任何模式，則存在異方差。 通常，這些值會隨著擬合值的增加而增加，從而形成錐形曲線。

閱讀：機器學習項目理念

異方差的通常原因

• 當變量中存在較大差異時。 換句話說，當變量中的最小值和最大值過於極端時。 這些也可能是異常值。
• 當您安裝錯誤的模型時。 如果將線性回歸模型擬合到非線性數據，則會導致異方差。
• 當變量中值的比例不同時。
• 當數據的錯誤轉換用於回歸時。
• 當數據中存在左/右偏度時。

純與非純異方差

現在由於上述原因，異方差可以是純的或不純的。 當我們擬合正確的模型（線性或非線性）並且在殘差中仍然存在可見模式時，則稱為純異方差。

但是，如果我們擬合了錯誤的模型，然後觀察到殘差中的模式，那麼這就是不純異方差的情況。 根據異方差的類型，需要採取措施來克服它。 它還取決於您正在工作的域，並且因域而異。

機器學習中異方差的影響

正如我們之前討論的，線性回歸模型假設數據中存在同方差性。 如果這個假設被打破，那麼我們將無法相信我們得到的結果。

如果存在異方差，那麼具有高方差的實例將對我們不想要的預測產生更大的影響。

• 異方差的存在使係數不太精確，因此正確的係數離總體值更遠。
• 異方差性也可能產生小於實際值的 p 值。 這是因為係數估計的方差增加了，但標準 OLS（普通最小二乘）模型沒有檢測到它。 因此，OLS 模型使用低估的方差計算 p 值。 這可能導致我們錯誤地得出回歸係數顯著但實際上並不顯著的結論。
• 產生的標準誤差也會有偏差。 標準誤差對於計算重要檢驗和置信區間至關重要。 如果標準誤有偏差，則意味著測試不正確，回歸係數估計也不正確。

如何處理異方差？

如果您檢測到異方差的存在，那麼有多種方法可以解決它。 首先，讓我們考慮一個示例，其中有 2 個變量：城市人口和 COVID-19 感染人數。

現在在這個例子中，大城市與小三線城市的感染人數將存在巨大差異。 變量感染數將是獨立的，而城市人口將是因變量。

考慮將回歸模型擬合到該數據並觀察類似於上圖的異方差性。 所以現在我們知道模型中存在異方差性，需要對其進行修復。

現在第一步是確定異方差的來源。 在我們的例子中，它是具有較大方差的變量。

可以有多種方法來處理異方差性，但我們將研究三種這樣的方法。

操縱變量

我們可以對必須的變量/特徵進行一些修改，以減少這種大方差對模型預測的影響。 一種方法是通過將特徵修改為比率和百分比而不是實際值。

這將使功能傳達一些不同的信息，但值得嘗試。 是否可以實施這種方法也將取決於問題和數據。

這種方法對特徵的修改最少，通常有助於解決問題，甚至在某些情況下使模型的性能更好。

所以在我們的例子中，我們可以將特徵“感染數”更改為“感染率”。 這將有助於減少差異，因為很明顯，人口眾多的城市中的感染人數會很大。

加權回歸

加權回歸是對正態回歸的修改，其中數據點根據其方差分配一定的權重。 方差大的權重小，方差小的權重大。

因此，當這些權重平方時，小權重的平方低估了高方差的影響。

當使用正確的權重時，異方差性被同方差性取代。 但是如何找到正確的權重？ 一種快速的方法是使用該變量的倒數作為權重。

所以在我們的例子中，權重將是城市人口的倒數。

轉型

轉換數據是最後的手段，因為這樣做會失去功能的可解釋性。

這意味著您不再可以輕鬆地解釋該功能所顯示的內容。

一種方法是使用 Box-Cox 變換和對數變換。

在你走之前

數據中的異方差性可能有很多原因。 它也因一個域而異。

因此，在開始上述過程以消除異方差之前，了解這一點也很重要。

在這篇博客中，我們討論了同方差性和異方差性，以及如何使用它來實現多種機器學習算法。

如果您有興趣了解有關機器學習的更多信息，請查看 IIIT-B 和 upGrad 的機器學習和 AI 執行 PG 計劃，該計劃專為工作專業人士設計，提供 450 多個小時的嚴格培訓、30 多個案例研究和作業、IIIT -B 校友身份，5 個以上實用的實踐頂點項目和頂級公司的工作協助。