Omoscedasticità nell'apprendimento automatico: rilevamento, effetti e come trattare

Alla fine di questo tutorial, avrai conoscenza di quanto segue:

• Che cos'è l'omoscedasticità e l'eteroscedasticità?
• Come sapere se l'eteroscedasticità è presente.
• Effetti dell'eteroscedasticità nell'apprendimento automatico.
• Trattare l'eteroscedasticità.

Che cos'è l'omoscedasticità e l'eteroscedasticità?

Omoscedasticità significa essere della “stessa varianza”. Nella regressione lineare, una delle ipotesi principali è che vi sia un'omoscedasticità presente negli errori o nei termini residui (Y_Pred – Y_actual).

In altre parole, la regressione lineare presuppone che per tutte le istanze i termini di errore siano gli stessi e con una varianza minima.

Capiamolo con l'aiuto di un esempio. Considera che abbiamo due variabili: l'area del tappeto della casa e il prezzo della casa. Con l'aumento della superficie del tappeto, aumentano anche i prezzi.

Quindi adattiamo un modello di regressione lineare e vediamo che gli errori hanno la stessa varianza in tutto. Il grafico nell'immagine sottostante ha Area tappeto sull'asse X e Prezzo sull'asse Y.

Come puoi vedere, le previsioni sono quasi lungo la linea di regressione lineare e con una varianza simile in tutto.

Inoltre, se tracciamo questi residui sull'asse X, lo vedremmo lungo una linea retta parallela all'asse X. Questo è un chiaro segno di omoscedasticità

Fonte immagine

Quando questa condizione viene violata, significa che c'è eteroschedasticità nel modello. Considerando lo stesso esempio di cui sopra, diciamo che per le case con area di moquette minore gli errori o residui o molto piccoli. E all'aumentare dell'area del tappeto, aumenta la varianza nelle previsioni, il che si traduce in un aumento del valore dell'errore o dei termini residui. Quando tracciamo nuovamente i valori vediamo la tipica curva Cone che indica fortemente la presenza di eteroscedsticità nel modello.

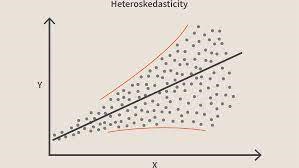
Fonte immagineIn particolare, l'eteroscedasticità è un aumento o una diminuzione sistematica della varianza dei residui nell'intervallo di variabili indipendenti. Questo è un problema perché l'omoscedasticità è un presupposto di regressione lineare e tutti gli errori dovrebbero essere della stessa varianza. Ulteriori informazioni sulla regressione lineare

Partecipa al corso di Machine Learning online dalle migliori università del mondo: master, programmi post-laurea per dirigenti e programma di certificazione avanzato in ML e AI per accelerare la tua carriera.

Come sapere se l'eteroscedasticità è presente?

In parole povere, il modo più semplice per sapere se l'eteroscedasticità è presente è tracciare il grafico dei residui. Se vedi qualche modello presente, allora c'è l'eteroscedasticità. Tipicamente i valori aumentano all'aumentare del valore adattato, creando così una curva a forma di cono.

Leggi: Idee per progetti di apprendimento automatico

Ragioni usuali per eteroschedasticità

• Quando c'è una grande varianza in una variabile. In altre parole, quando i valori più piccoli e più grandi in una variabile sono troppo estremi. Questi possono anche essere valori anomali.
• Quando stai montando il modello sbagliato. Se si adatta un modello di regressione lineare a un dato che non è lineare, si verificherà l'eteroscedasticità.
• Quando la scala dei valori in una variabile non è la stessa.
• Quando una trasformazione errata sui dati viene utilizzata per la regressione.
• Quando è presente un'asimmetria sinistra/destra nei dati.

Eteroscedasticità pura contro impura

Ora, con le ragioni di cui sopra, l'eteroscedasticità può essere pura o impura. Quando adattiamo il modello giusto (lineare o non lineare) e se c'è ancora un modello visibile nei residui, allora si parla di eteroschedasticità pura.

Tuttavia, se adattiamo il modello sbagliato e poi osserviamo un modello nei residui, allora è un caso di eteroschedasticità impura. A seconda del tipo di eteroschedasticità è necessario adottare misure per superarla. Dipende anche dal dominio in cui stai lavorando e varia da dominio a dominio.

Effetti dell'eteroscedasticità nell'apprendimento automatico

Come discusso in precedenza, il modello di regressione lineare fa un'ipotesi sulla presenza dell'omoscedasticità nei dati. Se questo presupposto viene infranto, non saremo in grado di fidarci dei risultati che otteniamo.

Se l'eteroscedasticità è presente, le istanze con varianza elevata avranno un impatto maggiore sulla previsione che non vogliamo.

• La presenza di eteroschedasticità rende i coefficienti meno precisi e quindi i coefficienti corretti sono più lontani dal valore della popolazione.
• È probabile che anche l'eteroscedasticità produca valori p inferiori ai valori effettivi. Ciò è dovuto al fatto che la varianza delle stime dei coefficienti è aumentata ma il modello standard OLS (Ordinary Least Squares) non l'ha rilevata. Pertanto il modello OLS calcola i valori p utilizzando una varianza sottostimata. Questo può portarci a concludere erroneamente che i coefficienti di regressione sono significativi quando in realtà non sono significativi.
• Anche gli errori standard prodotti saranno distorti. Gli errori standard sono cruciali nel calcolo dei test significativi e degli intervalli di confidenza. Se gli errori standard sono distorti, significa che i test non sono corretti e le stime del coefficiente di regressione saranno errate.

Come trattare l'eteroscedasticità?

Se rilevi la presenza di eteroschedasticità, allora ci sono diversi modi per affrontarla. Per prima cosa, consideriamo un esempio in cui abbiamo 2 variabili: Popolazione della città e Numero di infezioni da COVID-19.

Ora, in questo esempio, ci sarà un'enorme differenza nel numero di infezioni nelle grandi città metropolitane rispetto alle piccole città di livello 3. La variabile Numero di infezioni sarà indipendente e Popolazione della città sarà una variabile dipendente.

Considera che adatta un modello di regressione a questi dati e osserva l'eteroscedasticità simile all'immagine sopra. Quindi ora sappiamo che nel modello è presente l'eteroscedasticità e deve essere risolta.

Ora il primo passo sarebbe identificare la fonte dell'eteroscedasticità. Nel nostro caso, è la variabile con una grande varianza.

Ci possono essere diversi modi per affrontare l'eteroscedasticità, ma esamineremo tre di questi metodi.

Manipolazione delle variabili

Possiamo apportare alcune modifiche alle variabili/caratteristiche che abbiamo per ridurre l'impatto di questa grande varianza sulle previsioni del modello. Un modo per farlo modificando le caratteristiche su tariffe e percentuali anziché sui valori effettivi.

Ciò farebbe sì che le funzionalità trasmettano informazioni leggermente diverse, ma vale la pena provare. Dipenderà anche dal problema e dai dati se questo tipo di approccio può essere implementato o meno.

Questo metodo comporta la minima modifica con le funzionalità e spesso aiuta a risolvere il problema e in alcuni casi anche a migliorare le prestazioni del modello.

Quindi, nel nostro caso, possiamo cambiare la funzione "Numero di infezioni" in "Tasso di infezioni". Ciò contribuirà a ridurre la varianza poiché ovviamente il numero di infezioni nelle città con una popolazione numerosa sarà elevato.

Regressione ponderata

La regressione ponderata è una modifica della regressione normale in cui ai punti dati vengono assegnati determinati pesi in base alla loro varianza. A quelli con varianza grande vengono dati pesi piccoli e quelli con varianza minore pesi maggiori.

Quindi, quando questi pesi sono al quadrato, il quadrato dei pesi piccoli sottostima l'effetto della varianza elevata.

Quando vengono utilizzati i pesi corretti, l'eteroscedasticità viene sostituita dall'omoscedasticità. Ma come trovare i pesi corretti? Un modo rapido è usare l'inverso di quella variabile come peso.

Quindi nel nostro caso, il peso sarà Inverse of City Population.

Trasformazioni

Trasformare i dati è l'ultima risorsa in quanto così facendo si perde l'interpretabilità della caratteristica.

Ciò significa che non puoi più spiegare facilmente cosa mostra la funzione.

Un modo potrebbe essere quello di utilizzare le trasformazioni Box-Cox e le trasformazioni log.

Prima che tu vada

Ci possono essere molte ragioni per l'eteroscedasticità nei tuoi dati. Inoltre varia molto da un dominio all'altro.

Quindi è essenziale conoscerlo anche prima di iniziare con i processi di cui sopra per rimuovere l'eteroscedasticità.

In questo blog, abbiamo discusso di omoscedasticità ed eteroschedasticità e di come possono essere utilizzate per implementare diversi algoritmi di apprendimento automatico.

Se sei interessato a saperne di più sull'apprendimento automatico, dai un'occhiata al programma Executive PG di IIIT-B e upGrad in Machine Learning e AI , progettato per i professionisti che lavorano e offre oltre 450 ore di formazione rigorosa, oltre 30 casi di studio e incarichi, IIIT -B Status di Alumni, oltre 5 progetti pratici pratici e assistenza sul lavoro con le migliori aziende.