Homocedasticidade no aprendizado de máquina: detecção, efeitos e como tratar

Ao final deste tutorial, você terá conhecimento do seguinte:

• O que é Homocedasticidade e Heterocedasticidade?
• Como saber se a heterocedasticidade está presente.
• Efeitos da Heterocedasticidade no Aprendizado de Máquina.
• Tratamento da heterocedasticidade.

O que é Homocedasticidade e Heterocedasticidade?

Homocedasticidade significa ser da “mesma variação”. Na Regressão Linear, um dos principais pressupostos é que existe uma Homocedasticidade presente nos erros ou nos termos residuais (Y_Pred – Y_actual).

Em outras palavras, a Regressão Linear assume que para todas as instâncias, os termos de erro serão os mesmos e de muito pouca variação.

Vamos entendê-lo com a ajuda de um exemplo. Considere que temos duas variáveis ​​– área do tapete da casa e preço da casa. À medida que a área do tapete aumenta, os preços também aumentam.

Então ajustamos um modelo de regressão linear e vemos que os erros têm a mesma variância em todos os aspectos. O gráfico na imagem abaixo tem a área do tapete no eixo X e o preço no eixo Y.

Como você pode ver, as previsões estão quase ao longo da linha de regressão linear e com variância semelhante por toda parte.

Além disso, se plotarmos esses resíduos no eixo X, veremos isso em uma linha reta paralela ao eixo X. Este é um sinal claro de homocedasticidade

Fonte da imagem

Quando esta condição é violada, significa que há Heterocedasticidade no modelo. Considerando o mesmo exemplo acima, digamos que para casas com área de carpete menor os erros ou resíduos ou muito pequenos. E à medida que a área do tapete aumenta, a variação nas previsões aumenta, o que resulta no aumento do valor do erro ou dos termos residuais. Quando plotamos os valores novamente, vemos a curva Cone típica que indica fortemente a presença de Heteroscedsticidade no modelo.

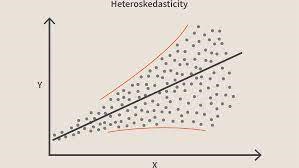
Fonte da imagemEspecificamente falando, a heterocedasticidade é um aumento ou diminuição sistemática na variância dos resíduos ao longo do intervalo de variáveis ​​independentes. Isso é um problema porque a homocedasticidade é uma suposição de regressão linear e todos os erros devem ter a mesma variância. Saiba mais sobre regressão linear

Participe do Curso de Aprendizado de Máquina on-line das principais universidades do mundo - Mestrados, Programas de Pós-Graduação Executiva e Programa de Certificado Avançado em ML e IA para acelerar sua carreira.

Como saber se a heterocedasticidade está presente?

Em termos mais simples, a maneira mais fácil de saber se a heterocedasticidade está presente é traçar o gráfico dos resíduos. Se você vir algum padrão presente, então há Heterocedasticidade. Normalmente, os valores aumentam à medida que o valor ajustado aumenta, fazendo assim uma curva em forma de cone.

Leia: Ideias de projetos de aprendizado de máquina

Razões usuais para a heterocedasticidade

• Quando há uma grande variação em uma variável. Em outras palavras, quando os valores menor e maior de uma variável são muito extremos. Estes também podem ser outliers.
• Quando você está ajustando o modelo errado. Se você ajustar um modelo de regressão linear a um dado não linear, isso levará à heterocedasticidade.
• Quando a escala de valores em uma variável não é a mesma.
• Quando uma transformação errada nos dados é usada para regressão.
• Quando há assimetria esquerda/direita presente nos dados.

Heterocedasticidade pura vs impura

Agora com as razões acima, a Heterocedasticidade pode ser Pura ou Impura. Quando ajustamos o modelo correto (linear ou não linear) e se ainda existe um padrão visível nos resíduos então é chamado de Heterocedasticidade Pura.

No entanto, se ajustarmos o modelo errado e observarmos um padrão nos resíduos, então é um caso de Heterocedasticidade Impura. Dependendo do tipo de heterocedasticidade as medidas precisam ser tomadas para superá-la. Também depende do domínio em que você está trabalhando e varia de domínio para domínio.

Efeitos da heterocedasticidade no aprendizado de máquina

Como discutimos anteriormente, o modelo de regressão linear faz uma suposição sobre a presença de homocedasticidade nos dados. Se essa suposição for quebrada, não poderemos confiar nos resultados que obtemos.

Se a heterocedasticidade estiver presente, as instâncias com alta variância terão um impacto maior na previsão que não queremos.

• A presença de heterocedasticidade torna os coeficientes menos precisos e, portanto, os coeficientes corretos estão mais distantes do valor da população.
• A heterocedasticidade também pode produzir valores de p menores do que os valores reais. Isso se deve ao fato de que a variância das estimativas dos coeficientes aumentou, mas o modelo padrão OLS (Ordinary Least Squares) não a detectou. Portanto, o modelo OLS calcula os valores de p usando uma variância subestimada. Isso pode nos levar a concluir incorretamente que os coeficientes de regressão são significativos quando na verdade não são significativos.
• Os erros padrão produzidos também serão tendenciosos. Os erros padrão são cruciais no cálculo de testes significativos e intervalos de confiança. Se os erros padrão forem tendenciosos, isso significará que os testes estão incorretos e as estimativas do coeficiente de regressão estarão incorretas.

Como tratar a heterocedasticidade?

Se você detectar a presença de heterocedasticidade, existem várias maneiras de lidar com isso. Primeiramente, vamos considerar um exemplo onde temos 2 variáveis: População da Cidade e Número de Infecções do COVID-19.

Agora, neste exemplo, haverá uma enorme diferença no número de infecções em grandes cidades metropolitanas versus pequenas cidades de nível 3. A variável Número de Infecções será independente e População da Cidade será uma variável dependente.

Considere que ajuste um modelo de regressão a esses dados e observe Heterocedasticidade semelhante à imagem acima. Então agora sabemos que há Heterocedasticidade presente no modelo e ela precisa ser corrigida.

Agora o primeiro passo seria identificar a fonte da Heterocedasticidade. No nosso caso, é a variável com uma grande variância.

Pode haver várias maneiras de lidar com a heterocedasticidade, mas veremos três desses métodos.

Manipulando as Variáveis

Podemos fazer algumas modificações nas variáveis/características que temos para reduzir o impacto dessa grande variação nas previsões do modelo. Uma maneira de fazer isso modificando os recursos para taxas e porcentagens em vez de valores reais.

Isso faria com que os recursos transmitissem informações um pouco diferentes, mas vale a pena tentar. Também dependerá do problema e dos dados se esse tipo de abordagem pode ser implementado ou não.

Este método envolve a menor modificação com recursos e muitas vezes ajuda a resolver o problema e até mesmo melhorar o desempenho do modelo em alguns casos.

Portanto, no nosso caso, podemos alterar o recurso “Número de infecções” para “Taxa de infecções”. Isso ajudará a reduzir a variação, pois obviamente o número de infecções em cidades com grande população será grande.

Regressão Ponderada

A regressão ponderada é uma modificação da regressão normal em que os pontos de dados recebem determinados pesos de acordo com sua variância. Aqueles com grande variância recebem pesos pequenos e aqueles com menor variância recebem pesos maiores.

Então, quando esses pesos são elevados ao quadrado, o quadrado dos pesos pequenos subestima o efeito da alta variância.

Quando os pesos corretos são usados, a Heterocedasticidade é substituída pela Homocedasticidade. Mas como encontrar pesos corretos? Uma maneira rápida é usar o inverso dessa variável como o peso.

Então, no nosso caso, o peso será o Inverso da População da Cidade.

Transformações

Transformar os dados é o último recurso, pois ao fazer isso você perde a interpretabilidade do recurso.

O que isso significa é que você não pode mais explicar facilmente o que o recurso está mostrando.

Uma maneira pode ser usar transformações Box-Cox e transformações de log.

Antes de você ir

Pode haver muitas razões para a heterocedasticidade em seus dados. Também varia muito de um domínio para outro.

Portanto, é essencial ter o conhecimento disso também antes de iniciar os processos acima para remover a heterocedasticidade.

Neste blog, discutimos Homocedasticidade e Heteroscedasticidade e como ela pode ser usada para implementar vários algoritmos de aprendizado de máquina.

Se você estiver interessado em aprender mais sobre aprendizado de máquina, confira o Programa PG Executivo do IIIT-B e do upGrad em Machine Learning e IA , projetado para profissionais que trabalham e oferece mais de 450 horas de treinamento rigoroso, mais de 30 estudos de caso e atribuições, IIIT -B Alumni status, mais de 5 projetos práticos práticos e assistência de trabalho com as principais empresas.