Homoscedasticity ในการเรียนรู้ของเครื่อง: การตรวจจับ ผลกระทบ และวิธีการรักษา

ในตอนท้ายของบทช่วยสอนนี้ คุณจะมีความรู้ดังต่อไปนี้:

• Homoscedasticity & Heteroscedasticity คืออะไร?
• จะทราบได้อย่างไรว่า Heteroscedasticity มีอยู่หรือไม่
• ผลกระทบของความแตกต่างในการเรียนรู้ของเครื่อง
• การรักษา heteroscedasticity

Homoscedasticity & Heteroscedasticity คืออะไร?

Homoscedasticity หมายถึง ความเป็น "ความแปรปรวนเดียวกัน" ในการถดถอยเชิงเส้น หนึ่งในสมมติฐานหลักคือมี Homoscedasticity อยู่ในข้อผิดพลาดหรือเงื่อนไขที่เหลือ (Y_Pred – Y_actual)

กล่าวอีกนัยหนึ่ง Linear Regression ถือว่าในทุกกรณี เงื่อนไขข้อผิดพลาดจะเหมือนกันและมีความแปรปรวนน้อยมาก

มาทำความเข้าใจกันโดยใช้ตัวอย่าง พิจารณาเรามีสองตัวแปร – พื้นที่พรมของบ้านและราคาของบ้าน. เมื่อพื้นที่พรมเพิ่มขึ้น ราคาก็เพิ่มขึ้นด้วย

เราจึงใส่แบบจำลองการถดถอยเชิงเส้นและเห็นว่าข้อผิดพลาดมีความแปรปรวนเท่ากันตลอด กราฟในภาพด้านล่างมีพื้นที่พรมในแกน X และราคาในแกน Y

อย่างที่คุณเห็น การคาดคะเนเกือบจะตามแนวการถดถอยเชิงเส้นและมีความแปรปรวนใกล้เคียงกันตลอด

นอกจากนี้ หากเราพลอตเศษที่เหลือเหล่านี้บนแกน X เราจะเห็นมันในแนวเส้นตรงขนานกับแกน X นี่เป็นสัญญาณที่ชัดเจนของ Homoscedasticity

ที่มาของภาพ

เมื่อเงื่อนไขนี้ถูกละเมิด หมายความว่ามีความแตกต่างในแบบจำลอง จากตัวอย่างเดียวกันกับข้างต้น สมมติว่าสำหรับบ้านที่มีพื้นที่ปูพรมน้อยกว่าจะมีข้อผิดพลาดหรือเศษเหลือหรือน้อยมาก และเมื่อพื้นที่พรมเพิ่มขึ้น ความแปรปรวนในการคาดคะเนก็จะเพิ่มขึ้น ซึ่งส่งผลให้ค่าของข้อผิดพลาดหรือค่าคงเหลือเพิ่มขึ้น เมื่อเราพลอตค่าอีกครั้ง เราจะเห็นกราฟ Cone ทั่วไป ซึ่งบ่งบอกถึงการมีอยู่ของเฮเทอรอสเซดซิซิตี้ในโมเดลอย่างชัดเจน

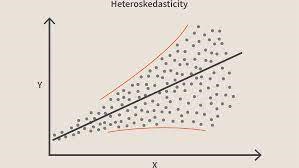
ที่มาของภาพโดยเฉพาะอย่างยิ่งการพูด Heteroscedasticity คือการเพิ่มขึ้นหรือลดลงอย่างเป็นระบบในความแปรปรวนของสารตกค้างในช่วงของตัวแปรอิสระ นี่เป็นปัญหาเนื่องจาก Homoscedasticity เป็นสมมติฐานของการถดถอยเชิงเส้น และข้อผิดพลาดทั้งหมดควรมีความแปรปรวนเท่ากัน เรียนรู้เพิ่มเติมเกี่ยวกับการถดถอยเชิงเส้น

เข้าร่วม หลักสูตรแมชชีนเลิ ร์นนิง ออนไลน์จากมหาวิทยาลัยชั้นนำของโลก – ปริญญาโท หลักสูตร Executive Post Graduate และหลักสูตรประกาศนียบัตรขั้นสูงใน ML & AI เพื่อติดตามอาชีพของคุณอย่างรวดเร็ว

จะทราบได้อย่างไรว่ามีความแตกต่างกันหรือไม่?

ในแง่ที่ง่ายที่สุด วิธีที่ง่ายที่สุดที่จะทราบว่าค่าเฮเทอรอสซีดาสติกซิตี้มีอยู่หรือไม่ โดยการพล็อตกราฟของเศษเหลือ หากคุณเห็นรูปแบบใด ๆ แสดงว่ามีความเหลื่อมล้ำ โดยปกติ ค่าจะเพิ่มขึ้นเมื่อค่าที่พอดีเพิ่มขึ้น ซึ่งจะทำให้เส้นโค้งรูปกรวย

อ่าน: แนวคิดโครงการการเรียนรู้ของเครื่อง

เหตุผลทั่วไปสำหรับความต่างศักย์

• เมื่อมีความแปรปรวนมากในตัวแปร กล่าวอีกนัยหนึ่ง เมื่อค่าที่น้อยที่สุดและมากที่สุดในตัวแปรมีค่ามากเกินไป สิ่งเหล่านี้อาจเป็นค่าผิดปกติได้เช่นกัน
• เมื่อคุณใส่ผิดรุ่น หากคุณใส่ตัวแบบการถดถอยเชิงเส้นเข้ากับข้อมูลที่ไม่ใช่เชิงเส้น มันจะนำไปสู่
• เมื่อขนาดของค่าในตัวแปรไม่เท่ากัน
• เมื่อมีการใช้การแปลงข้อมูลที่ไม่ถูกต้องสำหรับการถดถอย
• เมื่อมีความเบ้ซ้าย/ขวาในข้อมูล

ความแตกต่างระหว่าง Pure Vs Impure Heteroscedasticity

ด้วยเหตุผลข้างต้นนี้ ความต่างศักย์สามารถเป็นได้ทั้งแบบบริสุทธิ์และไม่บริสุทธิ์ เมื่อเราใส่โมเดลที่เหมาะสม (เชิงเส้นหรือไม่เป็นเชิงเส้น) และหากยังมีรูปแบบที่มองเห็นได้ในตัวแบบที่เหลือก็จะเรียกว่า Pure Heteroscedasticity

อย่างไรก็ตาม หากเราใส่โมเดลที่ไม่ถูกต้องแล้วสังเกตรูปแบบในส่วนที่เหลือ แสดงว่าเป็นกรณีของ Impure Heteroscedasticity ต้องใช้มาตรการเพื่อเอาชนะทั้งนี้ขึ้นอยู่กับชนิดของ heteroscedasticity นอกจากนี้ยังขึ้นอยู่กับโดเมนที่คุณกำลังทำงานอยู่และแตกต่างกันไปในแต่ละโดเมน

ผลกระทบของความแตกต่างในการเรียนรู้ของเครื่อง

ดังที่เราได้กล่าวไว้ก่อนหน้านี้ ตัวแบบการถดถอยเชิงเส้นตั้งสมมติฐานเกี่ยวกับ Homoscedasticity ที่มีอยู่ในข้อมูล หากสมมติฐานนั้นขาดไป เราก็จะเชื่อถือผลลัพธ์ที่เราได้รับไม่ได้

หากมีความไม่เท่าเทียมกันเกิดขึ้น อินสแตนซ์ที่มีความแปรปรวนสูงจะมีผลกระทบมากขึ้นต่อการคาดคะเนซึ่งเราไม่ต้องการ

• การแสดงตนของความต่างศักย์ทำให้สัมประสิทธิ์แม่นยำน้อยลง และด้วยเหตุนี้สัมประสิทธิ์ที่ถูกต้องจึงอยู่ไกลจากค่าประชากร
• ความแตกต่างกันยังมีแนวโน้มที่จะสร้างค่า p ที่น้อยกว่าค่าจริง เนื่องจากค่าความแปรปรวนของการประมาณค่าสัมประสิทธิ์เพิ่มขึ้น แต่ตัวแบบมาตรฐาน OLS (Ordinary Least Squares) ตรวจไม่พบ ดังนั้น แบบจำลอง OLS จะคำนวณค่า p โดยใช้ค่าความแปรปรวนที่ประเมินต่ำเกินไป นี้สามารถทำให้เราสรุปอย่างไม่ถูกต้องว่าสัมประสิทธิ์การถดถอยมีนัยสำคัญเมื่อไม่มีนัยสำคัญจริงๆ
• ข้อผิดพลาดมาตรฐานที่เกิดขึ้นก็จะมีอคติเช่นกัน ข้อผิดพลาดมาตรฐานมีความสำคัญอย่างยิ่งในการคำนวณการทดสอบที่สำคัญและช่วงความเชื่อมั่น หากข้อผิดพลาดมาตรฐานมีความลำเอียง แสดงว่าการทดสอบไม่ถูกต้องและการประมาณค่าสัมประสิทธิ์การถดถอยจะไม่ถูกต้อง

วิธีการรักษา Heteroscedasticity?

หากคุณตรวจพบการมีอยู่ของ Heteroscedasticity แสดงว่ามีหลายวิธีที่จะจัดการกับมัน อันดับแรก ลองมาดูตัวอย่างที่เรามีตัวแปร 2 ตัว ได้แก่ ประชากรของเมือง และ จำนวนผู้ติดเชื้อ COVID-19

ในตัวอย่างนี้ จะมีความแตกต่างอย่างมากในจำนวนผู้ติดเชื้อในเมืองใหญ่และเมืองระดับ 3 ขนาดเล็ก ตัวแปร Number of Infections จะเป็นอิสระและจำนวนประชากรของเมืองจะเป็นตัวแปรตาม

พิจารณาว่าพอดีกับแบบจำลองการถดถอยกับข้อมูลนี้ และสังเกตความต่างศักย์ที่คล้ายกับภาพด้านบน ตอนนี้เรารู้แล้วว่ามีความต่างศักย์อยู่ในโมเดลและจำเป็นต้องแก้ไข

ตอนนี้ขั้นตอนแรกคือการระบุแหล่งที่มาของ Heteroscedasticity ในกรณีของเรา มันคือตัวแปรที่มีความแปรปรวนมาก

มีหลายวิธีในการจัดการกับ Heteroscedasticity แต่เราจะพิจารณาวิธีการดังกล่าวสามวิธี

การจัดการตัวแปร

เราสามารถปรับเปลี่ยนตัวแปร/คุณลักษณะบางอย่างได้ เพื่อลดผลกระทบของความแปรปรวนขนาดใหญ่นี้ในการทำนายแบบจำลอง วิธีหนึ่งในการทำเช่นนี้โดยการปรับเปลี่ยนคุณสมบัติเป็นอัตราและเปอร์เซ็นต์แทนที่จะเป็นค่าจริง

ซึ่งจะทำให้คุณลักษณะต่างๆ ถ่ายทอดข้อมูลที่แตกต่างกันเล็กน้อย แต่ก็คุ้มค่าที่จะลอง นอกจากนี้ยังจะขึ้นอยู่กับปัญหาและข้อมูลด้วยว่าแนวทางประเภทนี้สามารถนำไปใช้ได้หรือไม่

วิธีนี้เกี่ยวข้องกับการปรับเปลี่ยนคุณลักษณะน้อยที่สุด และมักจะช่วยแก้ปัญหา และทำให้ประสิทธิภาพของโมเดลดีขึ้นในบางกรณี

ดังนั้น ในกรณีของเรา เราสามารถเปลี่ยนฟีเจอร์ “จำนวนการติดเชื้อ” เป็น “อัตราการติดไวรัส” วิธีนี้จะช่วยลดความแปรปรวนได้ เนื่องจากจำนวนผู้ติดเชื้อในเมืองที่มีประชากรมากจะมีจำนวนมาก

การถดถอยถ่วงน้ำหนัก

การถดถอยแบบถ่วงน้ำหนักเป็นการแก้ไขการถดถอยปกติโดยที่จุดข้อมูลกำหนดน้ำหนักบางอย่างตามความแปรปรวนของจุดข้อมูล อันที่มีความแปรปรวนมากจะได้รับน้ำหนักที่น้อย และอันที่มีความแปรปรวนน้อยกว่าจะได้รับน้ำหนักที่มากขึ้น

ดังนั้นเมื่อตุ้มน้ำหนักเหล่านี้กำลังสอง กำลังสองของตุ้มน้ำหนักขนาดเล็กจะประเมินผลของความแปรปรวนสูงต่ำไป

เมื่อใช้ตุ้มน้ำหนักที่ถูกต้อง Heteroscedasticity จะถูกแทนที่ด้วย Homoscedasticity แต่จะค้นหาน้ำหนักที่ถูกต้องได้อย่างไร? วิธีหนึ่งที่รวดเร็วคือการใช้ค่าผกผันของตัวแปรนั้นเป็นน้ำหนัก

ในกรณีของเรา น้ำหนักจะเป็นผกผันของประชากรเมือง

การแปลงร่าง

การแปลงข้อมูลเป็นทางเลือกสุดท้าย โดยการทำเช่นนี้จะทำให้คุณสูญเสียความสามารถในการตีความของคุณลักษณะ

นั่นหมายความว่าคุณไม่สามารถอธิบายสิ่งที่แสดงคุณลักษณะนี้ได้ง่ายๆ อีกต่อไป

วิธีหนึ่งอาจเป็นการใช้การแปลง Box-Cox และการแปลงบันทึก

ก่อนที่คุณจะไป

อาจมีสาเหตุหลายประการที่ทำให้ข้อมูลของคุณไม่เท่ากัน นอกจากนี้ยังแตกต่างกันอย่างมากจากโดเมนหนึ่งไปอีกโดเมนหนึ่ง

ดังนั้นจึงเป็นสิ่งสำคัญที่จะต้องมีความรู้เกี่ยวกับสิ่งนั้นเช่นกัน ก่อนที่คุณจะเริ่มด้วยกระบวนการข้างต้นเพื่อลบ Heteroscedasticity

ในบล็อกนี้ เราได้พูดถึง Homoscedasticity และ Heteroscedasticity และวิธีที่สามารถนำมาใช้เพื่อปรับใช้อัลกอริธึมการเรียนรู้ของเครื่องหลายตัว

หากคุณสนใจที่จะเรียนรู้เพิ่มเติมเกี่ยวกับแมชชีนเลิร์นนิง โปรดดูที่ IIIT-B & upGrad's Executive PG Program in Machine Learning & AI ซึ่งออกแบบมาสำหรับมืออาชีพที่ทำงานและมีการฝึกอบรมที่เข้มงวดมากกว่า 450 ชั่วโมง กรณีศึกษาและการมอบหมายมากกว่า 30 รายการ IIIT -B สถานะศิษย์เก่า 5+ โครงการหลักที่ปฏิบัติได้จริง & ความช่วยเหลืองานกับ บริษัท ชั้นนำ