機械学習における等分散性：検出、効果、および処理方法

このチュートリアルを終了するまでに、次の知識が身に付きます。

• 等分散性と不均一分散性とは何ですか？
• 不均一分散が存在するかどうかを知る方法。
• 機械学習における不均一分散の影響。
• 不均一分散の処理。

等分散性と不均一分散性とは何ですか？

等分散性とは、「同じ分散」であることを意味します。 線形回帰では、主な仮定の1つは、誤差または残余項（Y_Pred – Y_actual）に等分散性が存在することです。

言い換えると、線形回帰は、すべてのインスタンスで、誤差項が同じで分散がほとんどないと想定しています。

例を使って理解しましょう。 家のカーペットの面積と家の価格の2つの変数があると考えてください。 カーペットの面積が増えると、価格も上がります。

したがって、線形回帰モデルを当てはめて、エラーが全体を通して同じ分散であることがわかります。 下の画像のグラフは、X軸にカーペット面積、Y軸に価格があります。

ご覧のとおり、予測はほぼ線形回帰直線に沿っており、全体を通して同様の分散があります。

また、これらの残差をX軸にプロットすると、X軸に平行な直線に沿って表示されます。 これは等分散性の明らかな兆候です

画像ソース

この条件に違反すると、モデルに不均一分散が存在することを意味します。 上記と同じ例を考えて、カーペットの面積が少ない家の場合、エラーや残差、または非常に小さいとしましょう。 また、カーペットの面積が増えると、予測の分散が大きくなり、その結果、誤差または残差項の値が大きくなります。 値を再度プロットすると、モデルに異質性が存在することを強く示す典型的な円錐曲線が表示されます。

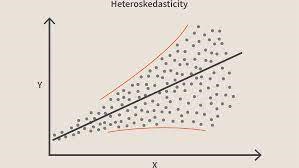
画像ソース具体的には、不均一分散は、独立変数の範囲にわたる残差の分散の体系的な増加または減少です。 等分散性は線形回帰の仮定であり、すべての誤差は同じ分散でなければならないため、これは問題です。 線形回帰の詳細

世界のトップ大学（修士、エグゼクティブ大学院プログラム、ML＆AIの高度な証明書プログラム）からオンラインで機械学習コースに参加して、キャリアを早急に進めましょう。

不均一分散が存在するかどうかを知る方法は？

簡単に言えば、不均一分散が存在するかどうかを知る最も簡単な方法は、残差のグラフをプロットすることです。 パターンが存在する場合は、不均一分散があります。 通常、値は近似値が増加するにつれて増加し、それによって円錐形の曲線を作成します。

読む：機械学習プロジェクトのアイデア

不均一分散の通常の理由

• 変数に大きな分散がある場合。 つまり、変数の最小値と最大値が極端すぎる場合です。 これらは外れ値である可能性もあります。
• 間違ったモデルを取り付けている場合。 線形回帰モデルを非線形のデータに当てはめると、不均一分散につながります。
• 変数の値のスケールが同じでない場合。
• データの誤った変換が回帰に使用された場合。
• データに左右の歪度が存在する場合。

純粋な対不均一な不均一分散

上記の理由により、不均一分散は純粋または不純のいずれかになります。 適切なモデル（線形または非線形）を適合させ、それでも残差に目に見えるパターンがある場合、それは純粋な不均一分散と呼ばれます。

ただし、間違ったモデルを適合させてから残差のパターンを観察すると、不純な不均一分散の場合になります。 不均一分散のタイプに応じて、それを克服するための対策を講じる必要があります。 また、作業しているドメインによって異なり、ドメインごとに異なります。

機械学習における不均一分散の影響

前に説明したように、線形回帰モデルは、データに等分散性が存在することを前提としています。 その仮定が破られた場合、私たちは得られた結果を信頼することができなくなります。

不均一分散が存在する場合、分散が大きいインスタンスは、予測に大きな影響を与えますが、これは望ましくありません。

• 不均一分散が存在すると、係数の精度が低下するため、正しい係数は母集団の値からさらに離れます。
• 不均一分散は、実際の値よりも小さいp値を生成する可能性もあります。 これは、係数推定値の分散が増加したが、標準のOLS（通常最小二乗）モデルがそれを検出しなかったためです。 したがって、OLSモデルは、過小評価された分散を使用してp値を計算します。 これにより、実際には有意ではないのに回帰係数が有意であるという誤った結論を下す可能性があります。
• 生成される標準エラーにもバイアスがかかります。 標準誤差は、重要なテストと信頼区間を計算する上で非常に重要です。 標準誤差にバイアスがかかっている場合は、テストが正しくなく、回帰係数の推定値が正しくないことを意味します。

不均一分散をどのように扱うか？

不均一分散の存在を検出した場合、それに取り組むには複数の方法があります。 まず、都市の人口とCOVID-19の感染数という2つの変数がある例を考えてみましょう。

この例では、大都市と小Tier3都市の感染数に大きな違いがあります。 変数の感染数は独立しており、都市の人口は従属変数になります。

回帰モデルをこのデータに適合させ、上の画像と同様の不均一分散を観察することを検討してください。 これで、モデルに不均一分散が存在し、修正する必要があることがわかりました。

ここで、最初のステップは、不均一分散の原因を特定することです。 私たちの場合、それは大きな分散を持つ変数です。

不均一分散に対処するには複数の方法がありますが、そのような3つの方法を見ていきます。

変数の操作

モデルの予測に対するこの大きな分散の影響を減らすために必要な変数/機能にいくつかの変更を加えることができます。 これを行う1つの方法は、機能を実際の値ではなくレートとパーセンテージに変更することです。

これにより、機能が少し異なる情報を伝達するようになりますが、試す価値があります。 このタイプのアプローチを実装できるかどうかは、問題とデータにも依存します。

この方法では、機能の変更が最小限に抑えられ、問題の解決に役立つことが多く、場合によってはモデルのパフォーマンスが向上することもあります。

したがって、この場合、機能「感染数」を「感染率」に変更できます。 人口の多い都市での感染数が非常に多いことは明らかであるため、これは分散を減らすのに役立ちます。

加重回帰

加重回帰は、データポイントに分散に応じて特定の加重が割り当てられる、通常の回帰の修正です。 分散が大きいものには小さな重みが与えられ、分散が小さいものには大きな重みが与えられます。

したがって、これらの重みが2乗されると、小さな重みの2乗は、高分散の効果を過小評価します。

正しい重みが使用されると、不均一分散性は等分散性に置き換えられます。 しかし、正しい重みを見つける方法は？ 簡単な方法の1つは、その変数の逆数を重みとして使用することです。

したがって、この場合、重みは都市人口の逆数になります。

変換

データの変換は、機能の解釈可能性を失うことによる最後の手段です。

つまり、機能が何を示しているかを簡単に説明できなくなります。

1つの方法は、Box-Cox変換と対数変換を使用することです。

行く前に

データの不均一分散には多くの理由があります。 また、ドメインごとに大きく異なります。

したがって、不均一分散を除去するための上記のプロセスを開始する前に、その知識も持っていることが不可欠です。

このブログでは、等分散性と不均一分散性、およびそれらを使用していくつかの機械学習アルゴリズムを実装する方法について説明しました。

機械学習について詳しく知りたい場合は、IIIT-BとupGradの機械学習とAIのエグゼクティブPGプログラムをご覧ください。このプログラムは、働く専門家向けに設計されており、450時間以上の厳格なトレーニング、30以上のケーススタディと課題、IIITを提供しています。 -B卒業生のステータス、5つ以上の実践的なキャップストーンプロジェクト、トップ企業との雇用支援。