机器学习中的同方差性：检测、影响和如何治疗

在本教程结束时，您将了解以下内容：

• 什么是同方差和异方差？
• 如何知道是否存在异方差。
• 机器学习中异方差的影响。
• 处理异方差。

什么是同方差和异方差？

Homoscedasticity 意味着具有“相同的方差”。 在线性回归中，主要假设之一是误差或残差项（Y_Pred – Y_actual）中存在同方差性。

换句话说，线性回归假设对于所有实例，误差项都是相同的并且方差很小。

让我们借助一个例子来理解它。 考虑我们有两个变量——房子的地毯面积和房子的价格。 随着地毯面积的增加，价格也随之上涨。

因此，我们拟合了一个线性回归模型，并看到误差自始至终具有相同的方差。 下图中的图表 X 轴为地毯面积，Y 轴为价格。

如您所见，预测几乎沿着线性回归线，并且始终具有相似的方差。

此外，如果我们在 X 轴上绘制这些残差，我们会看到它沿着平行于 X 轴的直线。 这是同方差性的明显标志

图片来源

当违反这个条件时，意味着模型中存在异方差。 考虑与上述相同的示例，假设对于地毯面积较小的房屋，误差或残差或非常小。 并且随着地毯面积的增加，预测的方差增加，这导致误差或残差项的值增加。 当我们再次绘制这些值时，我们会看到典型的圆锥曲线，这强烈表明模型中存在异方差。

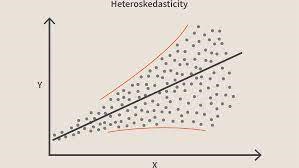
图片来源具体来说，异方差是自变量范围内残差方差的系统性增加或减少。 这是一个问题，因为同方差性是线性回归的假设，所有误差都应该具有相同的方差。 了解有关线性回归的更多信息

加入来自世界顶级大学的在线机器学习课程——硕士、高管研究生课程和 ML 和 AI 高级证书课程，以加快您的职业生涯。

如何知道是否存在异方差？

用最简单的术语来说，了解是否存在异方差的最简单方法是绘制残差图。 如果您看到存在任何模式，则存在异方差。 通常，这些值会随着拟合值的增加而增加，从而形成锥形曲线。

阅读：机器学习项目理念

异方差的通常原因

• 当变量中存在较大差异时。 换句话说，当变量中的最小值和最大值过于极端时。 这些也可能是异常值。
• 当您安装错误的模型时。 如果将线性回归模型拟合到非线性数据，则会导致异方差。
• 当变量中值的比例不同时。
• 当数据的错误转换用于回归时。
• 当数据中存在左/右偏度时。

纯与非纯异方差

现在由于上述原因，异方差可以是纯的或不纯的。 当我们拟合正确的模型（线性或非线性）并且在残差中仍然存在可见模式时，则称为纯异方差。

但是，如果我们拟合了错误的模型，然后观察到残差中的模式，那么这就是不纯异方差的情况。 根据异方差的类型，需要采取措施来克服它。 它还取决于您正在工作的域，并且因域而异。

机器学习中异方差的影响

正如我们之前讨论的，线性回归模型假设数据中存在同方差性。 如果这个假设被打破，那么我们将无法相信我们得到的结果。

如果存在异方差，那么具有高方差的实例将对我们不想要的预测产生更大的影响。

• 异方差的存在使系数不太精确，因此正确的系数离总体值更远。
• 异方差性也可能产生小于实际值的 p 值。 这是因为系数估计的方差增加了，但标准 OLS（普通最小二乘）模型没有检测到它。 因此，OLS 模型使用低估的方差计算 p 值。 这可能导致我们错误地得出回归系数显着但实际上并不显着的结论。
• 产生的标准误差也会有偏差。 标准误差对于计算重要检验和置信区间至关重要。 如果标准误有偏差，则意味着测试不正确，回归系数估计也不正确。

如何处理异方差？

如果您检测到异方差的存在，那么有多种方法可以解决它。 首先，让我们考虑一个示例，其中有 2 个变量：城市人口和 COVID-19 感染人数。

现在在这个例子中，大城市与小三线城市的感染人数将存在巨大差异。 变量感染数将是独立的，而城市人口将是因变量。

考虑将回归模型拟合到该数据并观察类似于上图的异方差性。 所以现在我们知道模型中存在异方差性，需要对其进行修复。

现在第一步是确定异方差的来源。 在我们的例子中，它是具有较大方差的变量。

可以有多种方法来处理异方差性，但我们将研究三种这样的方法。

操纵变量

我们可以对必须的变量/特征进行一些修改，以减少这种大方差对模型预测的影响。 一种方法是通过将特征修改为比率和百分比而不是实际值。

这将使功能传达一些不同的信息，但值得尝试。 是否可以实施这种方法也将取决于问题和数据。

这种方法对特征的修改最少，通常有助于解决问题，甚至在某些情况下使模型的性能更好。

所以在我们的例子中，我们可以将特征“感染数”更改为“感染率”。 这将有助于减少差异，因为很明显，人口众多的城市中的感染人数会很大。

加权回归

加权回归是对正态回归的修改，其中数据点根据其方差分配一定的权重。 方差大的权重小，方差小的权重大。

因此，当这些权重平方时，小权重的平方低估了高方差的影响。

当使用正确的权重时，异方差性被同方差性取代。 但是如何找到正确的权重？ 一种快速的方法是使用该变量的倒数作为权重。

所以在我们的例子中，权重将是城市人口的倒数。

转型

转换数据是最后的手段，因为这样做会失去功能的可解释性。

这意味着您不再可以轻松地解释该功能所显示的内容。

一种方法是使用 Box-Cox 变换和对数变换。

在你走之前

数据中的异方差性可能有很多原因。 它也因一个域而异。

因此，在开始上述过程以消除异方差之前，了解这一点也很重要。

在这篇博客中，我们讨论了同方差性和异方差性，以及如何使用它来实现多种机器学习算法。

如果您有兴趣了解有关机器学习的更多信息，请查看 IIIT-B 和 upGrad 的机器学习和 AI 执行 PG 计划，该计划专为工作专业人士设计，提供 450 多个小时的严格培训、30 多个案例研究和作业、IIIT -B 校友身份，5 个以上实用的实践顶点项目和顶级公司的工作协助。