Homocedasticidad en el aprendizaje automático: detección, efectos y cómo tratar

Al final de este tutorial, tendrá conocimiento de lo siguiente:

• ¿Qué es la homocedasticidad y la heterocedasticidad?
• Cómo saber si la Heterocedasticidad está presente.
• Efectos de la heterocedasticidad en el aprendizaje automático.
• Tratamiento de la heterocedasticidad.

¿Qué es la homocedasticidad y la heterocedasticidad?

Homocedasticidad significa ser de “la misma varianza”. En Regresión Lineal, uno de los principales supuestos es que existe una Homocedasticidad presente en los errores o los términos residuales (Y_Pred – Y_actual).

En otras palabras, la regresión lineal asume que para todas las instancias, los términos de error serán los mismos y con muy poca variación.

Vamos a entenderlo con la ayuda de un ejemplo. Considere que tenemos dos variables: el área de la alfombra de la casa y el precio de la casa. A medida que aumenta el área de la alfombra, los precios también aumentan.

Así que ajustamos un modelo de regresión lineal y vemos que los errores tienen la misma varianza en todo momento. El gráfico en la imagen de abajo tiene Área de alfombra en el eje X y Precio en el eje Y.

Como puede ver, las predicciones están casi a lo largo de la línea de regresión lineal y con una variación similar en todas partes.

Además, si trazamos estos residuos en el eje X, lo veríamos en una línea recta paralela al eje X. Este es un claro signo de homocedasticidad.

Fuente de imagen

Cuando se viola esta condición, significa que hay Heterocedasticidad en el modelo. Considerando el mismo ejemplo anterior, digamos que para casas con menor área de alfombra los errores o residuos son muy pequeños. Y a medida que aumenta el área de la alfombra, aumenta la variación en las predicciones, lo que da como resultado un aumento del valor del error o términos residuales. Cuando graficamos los valores nuevamente, vemos la típica curva de cono que indica fuertemente la presencia de heteroscedsticidad en el modelo.

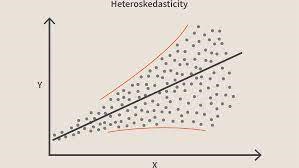
Fuente de imagenEspecíficamente hablando, la Heteroscedasticidad es un incremento o decremento sistemático en la varianza de los residuos sobre el rango de las variables independientes. Este es un problema porque la homocedasticidad es una suposición de regresión lineal y todos los errores deben tener la misma varianza. Obtenga más información sobre la regresión lineal

Únase al curso de aprendizaje automático en línea de las mejores universidades del mundo: maestrías, programas ejecutivos de posgrado y programa de certificado avanzado en ML e IA para acelerar su carrera.

¿Cómo saber si hay heterocedasticidad?

En los términos más simples, la forma más sencilla de saber si la Heteroscedasticidad está presente es trazando la gráfica de residuos. Si ve algún patrón presente, entonces hay heterocedasticidad. Normalmente, los valores aumentan a medida que aumenta el valor ajustado, formando así una curva en forma de cono.

Leer: Ideas de proyectos de aprendizaje automático

Razones usuales para la heterocedasticidad

• Cuando hay una gran variación en una variable. En otras palabras, cuando los valores más pequeños y más grandes de una variable son demasiado extremos. Estos también pueden ser valores atípicos.
• Cuando está ajustando el modelo equivocado. Si ajusta un modelo de regresión lineal a datos que no son lineales, dará lugar a heterocedasticidad.
• Cuando la escala de valores de una variable no es la misma.
• Cuando se usa una transformación incorrecta en los datos para la regresión.
• Cuando hay asimetría izquierda/derecha presente en los datos.

Heterocedasticidad pura vs impura

Ahora, con las razones anteriores, la heterocedasticidad puede ser pura o impura. Cuando ajustamos el modelo correcto (lineal o no lineal) y aún hay un patrón visible en los residuos, entonces se llama heteroscedasticidad pura.

Sin embargo, si ajustamos el modelo incorrecto y luego observamos un patrón en los residuos, entonces es un caso de heterocedasticidad impura. Dependiendo del tipo de Heterocedasticidad se deben tomar medidas para superarla. También depende del dominio en el que esté trabajando y varía de un dominio a otro.

Efectos de la heterocedasticidad en el aprendizaje automático

Como discutimos anteriormente, el modelo de regresión lineal asume que la homocedasticidad está presente en los datos. Si se rompe esa suposición, no podremos confiar en los resultados que obtengamos.

Si la heteroscedasticidad está presente, las instancias con una varianza alta tendrán un mayor impacto en la predicción que no queremos.

• La presencia de heterocedasticidad hace que los coeficientes sean menos precisos y, por lo tanto, los coeficientes correctos están más alejados del valor de la población.
• También es probable que la heterocedasticidad produzca valores p más pequeños que los valores reales. Esto se debe a que la varianza de las estimaciones de los coeficientes ha aumentado pero el modelo estándar OLS (Ordinary Least Squares) no lo detectó. Por lo tanto, el modelo OLS calcula los valores de p utilizando una varianza subestimada. Esto puede llevarnos a concluir incorrectamente que los coeficientes de regresión son significativos cuando en realidad no lo son.
• Los errores estándar producidos también estarán sesgados. Los errores estándar son cruciales para calcular pruebas significativas e intervalos de confianza. Si los errores estándar están sesgados, significará que las pruebas son incorrectas y las estimaciones del coeficiente de regresión serán incorrectas.

¿Cómo tratar la heterocedasticidad?

Si detecta la presencia de heterocedasticidad, existen varias formas de abordarla. Primero, consideremos un ejemplo donde tenemos 2 variables: Población de la Ciudad y Número de Infecciones de COVID-19.

Ahora, en este ejemplo, habrá una gran diferencia en la cantidad de infecciones en las grandes ciudades metropolitanas frente a las pequeñas ciudades de nivel 3. La variable Número de Infecciones será independiente y la Población de la Ciudad será una variable dependiente.

Considere que ajuste un modelo de regresión a estos datos y observe una heterocedasticidad similar a la imagen de arriba. Entonces, ahora sabemos que hay heterocedasticidad presente en el modelo y debe corregirse.

Ahora el primer paso sería identificar la fuente de heterocedasticidad. En nuestro caso, es la variable con una gran varianza.

Puede haber varias formas de lidiar con la heterocedasticidad, pero veremos tres de estos métodos.

Manipulando las variables

Podemos hacer algunas modificaciones a las variables/características que tenemos para reducir el impacto de esta gran variación en las predicciones del modelo. Una forma de hacerlo modificando las características a tasas y porcentajes en lugar de valores reales.

Esto haría que las funciones transmitieran información un poco diferente, pero vale la pena intentarlo. También dependerá del problema y los datos si este tipo de enfoque se puede implementar o no.

Este método implica la menor modificación con características y, a menudo, ayuda a resolver el problema e incluso mejora el rendimiento del modelo en algunos casos.

Entonces, en nuestro caso, podemos cambiar la función "Número de infecciones" a "Tasa de infecciones". Esto ayudará a reducir la varianza, ya que obviamente la cantidad de infecciones en ciudades con una gran población será grande.

Regresión ponderada

La regresión ponderada es una modificación de la regresión normal en la que a los puntos de datos se les asignan ciertos pesos de acuerdo con su varianza. A los que tienen una gran varianza se les asignan pesos pequeños y a los que tienen menos varianza se les asignan pesos más grandes.

Entonces, cuando estos pesos se elevan al cuadrado, el cuadrado de los pesos pequeños subestima el efecto de la varianza alta.

Cuando se utilizan los pesos correctos, la heterocedasticidad se reemplaza por la homocedasticidad. Pero, ¿cómo encontrar los pesos correctos? Una forma rápida es usar el inverso de esa variable como peso.

Entonces, en nuestro caso, el peso será el Inverso de la Población de la Ciudad.

Transformaciones

Transformar los datos es el último recurso, ya que al hacerlo se pierde la interpretabilidad de la función.

Lo que eso significa es que ya no puedes explicar fácilmente lo que muestra la función.

Una forma podría ser usar transformaciones de Box-Cox y transformaciones de registro.

Antes de que te vayas

Puede haber muchas razones para la heterocedasticidad en sus datos. También varía mucho de un dominio a otro.

Por lo tanto, es esencial tener conocimiento de eso también antes de comenzar con los procesos anteriores para eliminar la heterocedasticidad.

En este blog, discutimos la homocedasticidad y la heterocedasticidad y cómo se puede usar para implementar varios algoritmos de aprendizaje automático.

Si está interesado en obtener más información sobre el aprendizaje automático, consulte el Programa PG Ejecutivo en Aprendizaje Automático e IA de IIIT-B y upGrad, que está diseñado para profesionales que trabajan y ofrece más de 450 horas de capacitación rigurosa, más de 30 estudios de casos y asignaciones, IIIT -Estado de exalumno B, más de 5 proyectos prácticos finales prácticos y asistencia laboral con las mejores empresas.