Homoscedasticitatea în învățarea automată: detectarea, efectele și modul de tratare

Până la sfârșitul acestui tutorial, veți cunoaște următoarele:

• Ce este Homoscedasticitatea și Heteroscedasticitatea?
• Cum să știți dacă este prezentă heteroscedasticitatea.
• Efectele heteroscedasticității în învățarea automată.
• Tratarea heteroscedasticității.

Ce este homoscedasticitatea și heteroscedasticitatea?

Homoscedasticitatea înseamnă a fi de „aceeași variație”. În regresia liniară, una dintre ipotezele principale este că există o Homoscedasticitate prezentă în erori sau în termenii reziduali (Y_Pred – Y_actual).

Cu alte cuvinte, regresia liniară presupune că pentru toate cazurile, termenii de eroare vor fi aceiași și de foarte puțină variație.

Să-l înțelegem cu ajutorul unui exemplu. Luați în considerare că avem două variabile - suprafața covorului casei și prețul casei. Pe măsură ce suprafața covorului crește, cresc și prețurile.

Așadar, potrivim un model de regresie liniară și vedem că erorile sunt de aceeași varianță pe tot parcursul. Graficul din imaginea de mai jos are suprafața covorului pe axa X și prețul pe axa Y.

După cum puteți vedea, predicțiile sunt aproape de-a lungul liniei de regresie liniară și cu variații similare pe tot parcursul.

De asemenea, dacă am trasa aceste reziduuri pe axa X, le-am vedea de-a lungul unei linii drepte paralele cu axa X. Acesta este un semn clar de homocedasticitate

Sursa imaginii

Când această condiție este încălcată, înseamnă că există heteroscedasticitate în model. Luând în considerare același exemplu ca mai sus, să spunem că pentru casele cu suprafață mai mică de covoare erorile sau reziduurile sau foarte mici. Și pe măsură ce suprafața covorului crește, variația predicțiilor crește, ceea ce duce la creșterea valorii erorii sau a termenilor reziduali. Când trasăm din nou valorile, vedem curba tipică a conului, care indică puternic prezența heteroscedsticității în model.

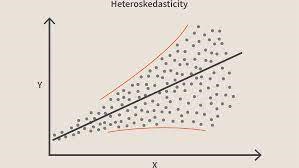
Sursa imaginiiVorbind în mod specific, heteroscedasticitatea este o creștere sau o scădere sistematică a varianței reziduurilor în intervalul de variabile independente. Aceasta este o problemă deoarece Homoscedasticitatea este o presupunere a regresiei liniare și toate erorile ar trebui să aibă aceeași varianță. Aflați mai multe despre regresia liniară

Alăturați-vă Cursului de învățare automată online de la cele mai bune universități din lume – Master, Programe Executive Postuniversitare și Program de Certificat Avansat în ML și AI pentru a vă accelera cariera.

Cum să știți dacă este prezentă heteroscedasticitatea?

În cei mai simpli termeni, cel mai simplu mod de a ști dacă este prezentă heteroscedasticitatea este prin reprezentarea graficului reziduurilor. Dacă vedeți vreun model prezent, atunci există heteroscedasticitate. De obicei, valorile cresc pe măsură ce valoarea ajustată crește, făcând astfel o curbă în formă de con.

Citiți: Idei de proiecte de învățare automată

Motive obișnuite pentru heteroscedasticitate

• Când există o variație mare într-o variabilă. Cu alte cuvinte, atunci când cele mai mici și cele mai mari valori dintr-o variabilă sunt prea extreme. Acestea pot fi, de asemenea, valori aberante.
• Când montați modelul greșit. Dacă potriviți un model de regresie liniară la o dată care este neliniară, va duce la heteroscedasticitate.
• Când scara valorilor dintr-o variabilă nu este aceeași.
• Când o transformare greșită a datelor este utilizată pentru regresie.
• Când există o asimetrie stânga/dreapta prezentă în date.

Heteroscedasticitatea pură vs. impură

Acum, din motivele de mai sus, heteroscedasticitatea poate fi fie pură, fie impură. Când ne potrivim pe modelul potrivit (liniar sau neliniar) și dacă încă există un model vizibil în reziduuri, atunci se numește heteroscedasticitate pură.

Cu toate acestea, dacă ne potrivim cu modelul greșit și apoi observăm un model în reziduuri, atunci este un caz de heteroscedasticitate impură. În funcție de tipul de heteroscedasticitate, trebuie luate măsuri pentru a o depăși. De asemenea, depinde de domeniul în care lucrați și variază de la un domeniu la altul.

Efectele heteroscedasticității în învățarea automată

După cum am discutat mai devreme, modelul de regresie liniară face o presupunere despre prezenta homocedasticității în date. Dacă această presupunere este încălcată, atunci nu vom putea avea încredere în rezultatele pe care le obținem.

Dacă este prezentă heteroscedasticitatea, atunci cazurile cu varianță mare vor avea un impact mai mare asupra predicției pe care nu o dorim.

• Prezența heteroscedasticității face coeficienții mai puțin precisi și, prin urmare, coeficienții corecti sunt mai departe de valoarea populației.
• Heteroscedasticitatea este, de asemenea, probabil să producă valori p mai mici decât valorile reale. Acest lucru se datorează faptului că varianța estimărilor coeficienților a crescut, dar modelul standard OLS (Ordinary Least Squares) nu a detectat-o. Prin urmare, modelul MOL calculează valorile p folosind o varianță subestimată. Acest lucru ne poate determina să facem incorect o concluzie că coeficienții de regresie sunt semnificativi atunci când de fapt nu sunt semnificativi.
• Erorile standard produse vor fi, de asemenea, părtinitoare. Erorile standard sunt cruciale în calcularea testelor semnificative și a intervalelor de încredere. Dacă erorile standard sunt părtinitoare, va însemna că testele sunt incorecte, iar estimările coeficientului de regresie vor fi incorecte.

Cum să tratăm heteroscedasticitatea?

Dacă detectați prezența heteroscedasticității, atunci există mai multe modalități de a o aborda. În primul rând, să luăm în considerare un exemplu în care avem 2 variabile: Populația orașului și numărul de infecții cu COVID-19.

Acum, în acest exemplu, va exista o diferență uriașă în numărul de infecții în orașele mari de metrou față de orașele mici de nivel 3. Variabila Număr de infecții va fi independentă, iar Populația orașului va fi o variabilă dependentă.

Luați în considerare că potriviți un model de regresie la aceste date și observați heteroscedasticitatea similară cu imaginea de mai sus. Deci acum știm că există heteroscedasticitate prezentă în model și trebuie remediată.

Acum, primul pas ar fi identificarea sursei heteroscedasticității. În cazul nostru, este variabila cu o varianță mare.

Pot exista mai multe moduri de a trata heteroscedasticitatea, dar ne vom uita la trei astfel de metode.

Manipularea variabilelor

Putem face unele modificări la variabilele/caracteristicile pe care le avem pentru a reduce impactul acestei variații mari asupra predicțiilor modelului. O modalitate de a face acest lucru prin modificarea caracteristicilor la rate și procente, mai degrabă decât la valori reale.

Acest lucru ar face ca funcțiile să transmită informații puțin diferite, dar merită încercat. De asemenea, va depinde de problemă și de date dacă acest tip de abordare poate fi implementat sau nu.

Această metodă implică cea mai mică modificare a caracteristicilor și ajută adesea la rezolvarea problemei și chiar la îmbunătățirea performanței modelului în unele cazuri.

Deci, în cazul nostru, putem schimba caracteristica „Număr de infecții” la „Rata de infecții”. Acest lucru va ajuta la reducerea varianței, deoarece, evident, numărul de infecții în orașele cu o populație mare va fi mare.

Regresia ponderată

Regresia ponderată este o modificare a regresiei normale în care punctelor de date li se atribuie anumite ponderi în funcție de variația lor. Celor cu varianță mare li se acordă ponderi mici, iar celor cu varianță mai mică li se acordă ponderi mai mari.

Deci, atunci când aceste ponderi sunt pătrate, pătratul ponderilor mici subestimează efectul varianței mari.

Când se utilizează ponderi corecte, heteroscedasticitatea este înlocuită cu homoscedasticitatea. Dar cum să găsești greutățile corecte? O modalitate rapidă este să utilizați inversul acelei variabile ca pondere.

Deci, în cazul nostru, ponderea va fi inversă a populației orașului.

Transformări

Transformarea datelor este ultima soluție, deoarece făcând asta pierzi interpretabilitatea caracteristicii.

Asta înseamnă că nu mai poți explica cu ușurință ce arată caracteristica.

O modalitate ar putea fi să folosești transformări Box-Cox și transformări jurnal.

Inainte sa pleci

Pot exista multe motive pentru heteroscedasticitatea în datele dvs. De asemenea, variază foarte mult de la un domeniu la altul.

Prin urmare, este esențial să cunoașteți acest lucru înainte de a începe cu procesele de mai sus pentru a elimina heteroscedasticitatea.

În acest blog, am discutat despre homoscedasticitate și heteroscedasticitate și despre cum poate fi folosită pentru a implementa mai mulți algoritmi de învățare automată.

Dacă sunteți interesat să aflați mai multe despre învățarea automată, consultați Programul Executive PG de la IIIT-B și upGrad în Învățare automată și IA, care este conceput pentru profesioniști care lucrează și oferă peste 450 de ore de pregătire riguroasă, peste 30 de studii de caz și sarcini, IIIT -B Statut de absolvenți, peste 5 proiecte practice practice și asistență pentru locuri de muncă cu firme de top.