Гомоскедастичность в машинном обучении: обнаружение, эффекты и способы лечения

К концу этого урока вы будете знать следующее:

• Что такое гомоскедастичность и гетероскедастичность?
• Как узнать, присутствует ли гетероскедастичность.
• Эффекты гетероскедастичности в машинном обучении.
• Лечение гетероскедастичности.

Что такое гомоскедастичность и гетероскедастичность?

Гомоскедастичность означает быть «одной и той же дисперсии». В линейной регрессии одно из основных предположений состоит в том, что в ошибках или остаточных терминах присутствует гомоскедастичность (Y_Pred – Y_actual).

Другими словами, линейная регрессия предполагает, что для всех случаев условия ошибки будут одинаковыми и будут иметь очень небольшие различия.

Давайте разберемся с помощью примера. Предположим, у нас есть две переменные — площадь ковра в доме и цена дома. С увеличением площади ковра растут и цены.

Таким образом, мы подгоняем модель линейной регрессии и видим, что ошибки везде имеют одинаковую дисперсию. График на изображении ниже имеет площадь ковра по оси X и цену по оси Y.

Как видите, прогнозы почти совпадают с линией линейной регрессии и имеют одинаковую дисперсию.

Кроме того, если мы нанесем эти остатки на ось X, мы увидим их вдоль прямой линии, параллельной оси X. Это явный признак гомоскедастичности.

Источник изображения

Когда это условие нарушается, значит, в модели присутствует гетероскедастичность. Рассматривая тот же пример, что и выше, допустим, что для домов с меньшей площадью ковра ошибки или невязки или очень малы. И по мере увеличения площади ковра увеличивается дисперсия в прогнозах, что приводит к увеличению значения ошибки или остаточных членов. Когда мы снова наносим значения на график, мы видим типичную кривую конуса, которая четко указывает на наличие гетероскестичности в модели.

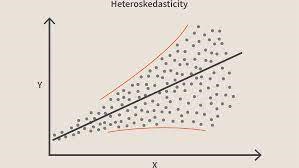
Источник изображенияВ частности, гетероскедастичность представляет собой систематическое увеличение или уменьшение дисперсии остатков в диапазоне независимых переменных. Это проблема, потому что гомоскедастичность является предположением линейной регрессии, и все ошибки должны иметь одинаковую дисперсию. Узнайте больше о линейной регрессии

Присоединяйтесь к онлайн- курсу по машинному обучению в ведущих университетах мира — магистерским программам, программам последипломного образования для руководителей и программам повышения квалификации в области машинного обучения и искусственного интеллекта, чтобы ускорить свою карьеру.

Как узнать, присутствует ли гетероскедастичность?

Проще говоря, самый простой способ узнать, присутствует ли гетероскедастичность, — построить график остатков. Если вы видите какой-либо паттерн, то это гетероскедастичность. Обычно значения увеличиваются по мере увеличения установленного значения, образуя, таким образом, конусообразную кривую.

Читайте: Идеи проекта машинного обучения

Обычные причины гетероскедастичности

• Когда есть большая дисперсия в переменной. Другими словами, когда наименьшее и наибольшее значения в переменной слишком экстремальны. Это также могут быть выбросы.
• Когда примеряешь не ту модель. Если вы подгоните модель линейной регрессии к нелинейным данным, это приведет к гетероскедастичности.
• Когда масштаб значений в переменной не одинаков.
• Когда для регрессии используется неправильное преобразование данных.
• Когда в данных присутствует асимметрия влево/вправо.

Чистая и нечистая гетероскедастичность

Теперь, по вышеуказанным причинам, гетероскедастичность может быть чистой или нечистой. Когда мы подбираем правильную модель (линейную или нелинейную) и если еще есть видимая закономерность в остатках, это называется чистой гетероскедастичностью.

Однако, если мы подбираем неправильную модель, а затем наблюдаем закономерность в остатках, то это случай нечистой гетероскедастичности. В зависимости от типа гетероскедастичности необходимо принимать меры по ее преодолению. Это также зависит от домена, в котором вы работаете, и варьируется от домена к домену.

Эффекты гетероскедастичности в машинном обучении

Как мы обсуждали ранее, модель линейной регрессии делает предположение о наличии в данных гомоскедастичности. Если это предположение будет нарушено, мы не сможем доверять полученным результатам.

Если присутствует гетероскедастичность, то экземпляры с высокой дисперсией будут иметь большее влияние на прогноз, чего мы не хотим.

• Наличие гетероскедастичности делает коэффициенты менее точными, и, следовательно, правильные коэффициенты находятся дальше от значения генеральной совокупности.
• Гетероскедастичность также может давать p-значения меньше, чем фактические значения. Это связано с тем, что дисперсия оценок коэффициентов увеличилась, но стандартная модель OLS (Обычные наименьшие квадраты) этого не обнаружила. Поэтому модель OLS вычисляет p-значения, используя заниженную дисперсию. Это может привести к неправильному выводу о том, что коэффициенты регрессии значимы, хотя на самом деле они не значимы.
• Полученные стандартные ошибки также будут смещены. Стандартные ошибки имеют решающее значение при расчете значимых тестов и доверительных интервалов. Если стандартные ошибки смещены, это будет означать, что тесты неверны, и оценки коэффициентов регрессии будут неверными.

Как лечить гетероскедастичность?

Если вы обнаружите наличие гетероскедастичности, то есть несколько способов справиться с ней. Во-первых, давайте рассмотрим пример, в котором у нас есть 2 переменные: население города и количество заражений COVID-19.

Теперь в этом примере будет огромная разница в количестве инфекций в крупных мегаполисах по сравнению с небольшими городами уровня 3. Переменная «Количество инфекций» будет независимой, а «Население города» — зависимой переменной.

Учтите, что подогнали регрессионную модель к этим данным и наблюдали гетероскедастичность, как на изображении выше. Итак, теперь мы знаем, что в модели присутствует гетероскедастичность, и ее необходимо исправить.

Теперь первым шагом будет выявление источника гетероскедастичности. В нашем случае это переменная с большой дисперсией.

Существует несколько способов борьбы с гетероскедастичностью, но мы рассмотрим три таких метода.

Управление переменными

Мы можем внести некоторые изменения в переменные/функции, которые у нас есть, чтобы уменьшить влияние этой большой дисперсии на прогнозы модели. Один из способов сделать это, изменив функции на ставки и проценты, а не на фактические значения.

Это заставило бы функции передавать немного другую информацию, но стоит попробовать. Это также будет зависеть от проблемы и данных, можно ли реализовать этот тип подхода или нет.

Этот метод предполагает наименьшее изменение функций и часто помогает решить проблему, а в некоторых случаях даже повысить производительность модели.

Так что в нашем случае мы можем изменить функцию «Количество заражений» на «Коэффициент заражений». Это поможет уменьшить дисперсию, так как совершенно очевидно, что количество инфекций в городах с большим населением будет большим.

Взвешенная регрессия

Взвешенная регрессия — это модификация обычной регрессии, при которой точкам данных присваиваются определенные веса в соответствии с их дисперсией. Те, у которых большая дисперсия, получают маленькие веса, а те, у которых меньше дисперсии, получают большие веса.

Таким образом, когда эти веса возводятся в квадрат, квадрат малых весов недооценивает эффект высокой дисперсии.

При использовании правильных весов гетероскедастичность заменяется гомоскедастичностью. Но как найти правильные веса? Одним из быстрых способов является использование обратной этой переменной в качестве веса.

Таким образом, в нашем случае вес будет обратным населению города.

Преобразования

Преобразование данных является последним средством, так как при этом вы теряете интерпретируемость функции.

Это означает, что вы больше не можете легко объяснить, что показывает эта функция.

Одним из способов может быть использование преобразований Бокса-Кокса и логарифмических преобразований.

Прежде чем ты уйдешь

Может быть много причин гетероскедастичности в ваших данных. Он также сильно варьируется от одного домена к другому.

Поэтому очень важно знать это, прежде чем вы начнете с вышеупомянутых процессов для устранения гетероскедастичности.

В этом блоге мы обсудили гомоскедастичность и гетероскедастичность и то, как их можно использовать для реализации нескольких алгоритмов машинного обучения.

Если вам интересно узнать больше о машинном обучении, ознакомьтесь с программой Executive PG IIIT-B и upGrad по машинному обучению и искусственному интеллекту , которая предназначена для работающих профессионалов и предлагает более 450 часов интенсивного обучения, более 30 тематических исследований и заданий, IIIT -B статус выпускника, 5+ практических практических проектов и помощь в трудоустройстве в ведущих фирмах.