Homoskedastizität beim maschinellen Lernen: Erkennung, Auswirkungen und Behandlung

Am Ende dieses Tutorials verfügen Sie über folgende Kenntnisse:

• Was ist Homoskedastizität und Heteroskedastizität?
• Wie kann man feststellen, ob Heteroskedastizität vorliegt?
• Auswirkungen der Heteroskedastizität beim maschinellen Lernen.
• Behandlung von Heteroskedastizität.

Was ist Homoskedastizität und Heteroskedastizität?

Homoskedastizität bedeutet, von „derselben Varianz“ zu sein. Bei der linearen Regression ist eine der Hauptannahmen, dass in den Fehlern oder Residualtermen (Y_Pred – Y_actual) eine Homoskedastizität vorhanden ist.

Mit anderen Worten, die lineare Regression geht davon aus, dass die Fehlerterme für alle Instanzen gleich und von sehr geringer Varianz sind.

Lassen Sie es uns anhand eines Beispiels verstehen. Stellen Sie sich vor, wir haben zwei Variablen – Teppichfläche des Hauses und Preis des Hauses. Mit zunehmender Teppichfläche steigen auch die Preise.

Wir passen also ein lineares Regressionsmodell an und sehen, dass die Fehler überall die gleiche Varianz haben. Das Diagramm im unteren Bild hat die Teppichfläche auf der X-Achse und den Preis auf der Y-Achse.

Wie Sie sehen können, liegen die Vorhersagen fast entlang der linearen Regressionslinie und weisen durchgehend eine ähnliche Varianz auf.

Wenn wir diese Residuen auf der X-Achse darstellen, sehen wir sie entlang einer geraden Linie parallel zur X-Achse. Dies ist ein klares Zeichen für Homoskedastizität

Bildquelle

Wenn diese Bedingung verletzt wird, bedeutet dies, dass das Modell Heteroskedastizität aufweist. Betrachten wir dasselbe Beispiel wie oben, nehmen wir an, dass bei Häusern mit geringerer Teppichfläche die Fehler oder Reste sehr klein sind. Und wenn die Teppichfläche zunimmt, nimmt die Varianz in den Vorhersagen zu, was zu einem zunehmenden Wert von Fehler- oder Resttermen führt. Wenn wir die Werte erneut darstellen, sehen wir die typische Kegelkurve, die stark auf das Vorhandensein von Heteroskedastizität im Modell hinweist.

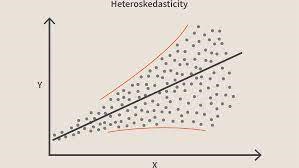
BildquelleGenauer gesagt ist Heteroskedastizität eine systematische Zunahme oder Abnahme der Varianz von Residuen über den Bereich unabhängiger Variablen. Dies ist ein Problem, da Homoskedastizität eine Annahme der linearen Regression ist und alle Fehler dieselbe Varianz haben sollten. Erfahren Sie mehr über lineare Regression

Nehmen Sie online am Machine Learning-Kurs der weltbesten Universitäten teil – Master, Executive Post Graduate Programs und Advanced Certificate Program in ML & AI, um Ihre Karriere zu beschleunigen.

Wie erkennt man, ob Heteroskedastizität vorliegt?

Vereinfacht gesagt lässt sich am einfachsten feststellen, ob Heteroskedastizität vorliegt, indem der Graph der Residuen gezeichnet wird. Wenn Sie irgendein Muster sehen, dann gibt es Heteroskedastizität. Typischerweise steigen die Werte, wenn der angepasste Wert zunimmt, wodurch eine kegelförmige Kurve entsteht.

Lesen Sie: Projektideen für maschinelles Lernen

Übliche Gründe für Heteroskedastizität

• Wenn eine Variable eine große Varianz aufweist. Mit anderen Worten, wenn der kleinste und der größte Wert in einer Variablen zu extrem sind. Dies können auch Ausreißer sein.
• Wenn Sie das falsche Modell montieren. Wenn Sie ein lineares Regressionsmodell an nichtlineare Daten anpassen, führt dies zu Heteroskedastizität.
• Wenn die Werteskala in einer Variablen nicht gleich ist.
• Wenn eine falsche Transformation von Daten für die Regression verwendet wird.
• Wenn in den Daten eine Links/Rechts-Schiefe vorhanden ist.

Reine vs. unreine Heteroskedastizität

Aus den oben genannten Gründen kann die Heteroskedastizität entweder rein oder unrein sein. Wenn wir das richtige Modell (linear oder nichtlinear) anpassen und es dennoch ein sichtbares Muster in den Residuen gibt, wird dies als reine Heteroskedastizität bezeichnet.

Wenn wir jedoch das falsche Modell anpassen und dann ein Muster in den Residuen beobachten, dann handelt es sich um einen Fall von unreiner Heteroskedastizität. Je nach Art der Heteroskedastizität müssen Maßnahmen ergriffen werden, um diese zu überwinden. Es hängt auch von der Domäne ab, in der Sie arbeiten, und variiert von Domäne zu Domäne.

Auswirkungen der Heteroskedastizität beim maschinellen Lernen

Wie bereits erwähnt, geht das lineare Regressionsmodell davon aus, dass Homoskedastizität in den Daten vorhanden ist. Wenn diese Annahme gebrochen wird, können wir den Ergebnissen, die wir erhalten, nicht vertrauen.

Wenn Heteroskedastizität vorhanden ist, haben die Instanzen mit hoher Varianz einen größeren Einfluss auf die Vorhersage, was wir nicht wollen.

• Das Vorhandensein von Heteroskedastizität macht die Koeffizienten weniger genau und daher sind die korrekten Koeffizienten weiter vom Populationswert entfernt.
• Heteroskedastizität führt wahrscheinlich auch zu p-Werten, die kleiner als die tatsächlichen Werte sind. Dies ist darauf zurückzuführen, dass die Varianz der Koeffizientenschätzungen zugenommen hat, das Standard-OLS-Modell (Ordinary Least Squares) dies jedoch nicht erkannt hat. Daher berechnet das OLS-Modell p-Werte mit einer unterschätzten Varianz. Dies kann dazu führen, dass wir fälschlicherweise den Schluss ziehen, dass die Regressionskoeffizienten signifikant sind, obwohl sie tatsächlich nicht signifikant sind.
• Die erzeugten Standardfehler sind ebenfalls verzerrt. Standardfehler sind entscheidend für die Berechnung signifikanter Tests und Konfidenzintervalle. Wenn die Standardfehler verzerrt sind, bedeutet dies, dass die Tests falsch sind und die Schätzungen der Regressionskoeffizienten falsch sind.

Wie behandelt man Heteroskedastizität?

Wenn Sie das Vorhandensein von Heteroskedastizität feststellen, gibt es mehrere Möglichkeiten, es anzugehen. Betrachten wir zunächst ein Beispiel, bei dem wir zwei Variablen haben: Bevölkerung der Stadt und Anzahl der COVID-19-Infektionen.

In diesem Beispiel wird es einen großen Unterschied in der Anzahl der Infektionen in großen Metrostädten im Vergleich zu kleinen Tier-3-Städten geben. Die Variable „Anzahl der Infektionen“ ist eine unabhängige Variable und die „Bevölkerung der Stadt“ eine abhängige Variable.

Berücksichtigen Sie, dass ein Regressionsmodell an diese Daten angepasst wird, und beobachten Sie die Heteroskedastizität ähnlich dem obigen Bild. Jetzt wissen wir also, dass im Modell Heteroskedastizität vorhanden ist, die behoben werden muss.

Nun wäre der erste Schritt, die Quelle der Heteroskedastizität zu identifizieren. In unserem Fall ist es die Variable mit großer Varianz.

Es kann mehrere Möglichkeiten geben, mit Heteroskedastizität umzugehen, aber wir werden uns drei solcher Methoden ansehen.

Manipulation der Variablen

Wir können einige Änderungen an den Variablen/Merkmale vornehmen, die wir haben, um die Auswirkungen dieser großen Varianz auf die Modellvorhersagen zu reduzieren. Eine Möglichkeit, dies zu tun, besteht darin, die Funktionen auf Raten und Prozentsätze statt auf tatsächliche Werte abzuändern.

Dies würde dazu führen, dass die Funktionen etwas andere Informationen vermitteln, aber es ist einen Versuch wert. Es hängt auch vom Problem und den Daten ab, ob diese Art von Ansatz implementiert werden kann oder nicht.

Diese Methode beinhaltet die wenigsten Änderungen an Features und hilft oft, das Problem zu lösen und in einigen Fällen sogar die Leistung des Modells zu verbessern.

In unserem Fall können wir also die Funktion „Anzahl der Infektionen“ in „Infektionsrate“ ändern. Dies wird dazu beitragen, die Varianz zu verringern, da die Zahl der Infektionen in Städten mit einer großen Bevölkerung ganz offensichtlich groß sein wird.

Gewichtete Regression

Die gewichtete Regression ist eine Modifikation der normalen Regression, bei der den Datenpunkten entsprechend ihrer Varianz bestimmte Gewichtungen zugewiesen werden. Diejenigen mit großer Varianz erhalten kleine Gewichte und diejenigen mit geringerer Varianz größere Gewichte.

Wenn diese Gewichte also quadriert werden, unterschätzt das Quadrat der kleinen Gewichte den Effekt der hohen Varianz.

Wenn korrekte Gewichtungen verwendet werden, wird Heteroskedastizität durch Homoskedastizität ersetzt. Aber wie finde ich die richtigen Gewichte? Eine schnelle Möglichkeit besteht darin, die Umkehrung dieser Variablen als Gewichtung zu verwenden.

In unserem Fall ist die Gewichtung also umgekehrt zur Stadtbevölkerung.

Transformationen

Das Transformieren der Daten ist der letzte Ausweg, da Sie dadurch die Interpretierbarkeit des Features verlieren.

Das bedeutet, dass Sie nicht mehr einfach erklären können, was die Funktion zeigt.

Eine Möglichkeit könnte darin bestehen, Box-Cox-Transformationen und Protokolltransformationen zu verwenden.

Bevor du gehst

Es kann viele Gründe für Heteroskedastizität in Ihren Daten geben. Es variiert auch stark von einer Domäne zur anderen.

Daher ist es wichtig, auch darüber Bescheid zu wissen, bevor Sie mit den oben genannten Prozessen beginnen, um Heteroskedastizität zu entfernen.

In diesem Blog haben wir Homoskedastizität und Heteroskedastizität diskutiert und wie sie zur Implementierung mehrerer Algorithmen für maschinelles Lernen verwendet werden können.

Wenn Sie mehr über maschinelles Lernen erfahren möchten, sehen Sie sich das Executive PG-Programm von IIIT-B & upGrad für maschinelles Lernen und KI an, das für Berufstätige konzipiert ist und mehr als 450 Stunden strenge Schulungen, mehr als 30 Fallstudien und Aufgaben, IIIT, bietet -B Alumni-Status, mehr als 5 praktische Schlusssteinprojekte und Arbeitsunterstützung bei Top-Unternehmen.