二項式定理：標準差、相關術語和性質

二項式定理是數學領域最常用的方程之一，在其他各個領域也有大量的應用。 二項式定理的一些實際應用包括：

• 將 IP 地址分配給計算機。
• 預測與國家經濟有關的各種因素。
• 天氣預報。
• 建築學。

二項式定理，有時也稱為二項式展開，用於統計、代數、概率以及其他各種數學和物理領域。 二項式定理由以下公式表示：

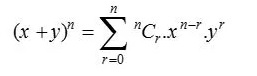
其中，n N 和 x,y R

資源

什麼是二項式實驗？

二項式定理公式通常用於計算二項式實驗結果的概率。 二項式實驗是一個只能有兩個結果的事件。 例如，預測某一天的降雨； 結果只能是兩種情況之一——要么那天下雨，要么那天不下雨。

由於一種情況只有兩個固定結果，因此稱為二項式實驗。 你可以在日常生活中找到很多二項式實驗的例子。 拋硬幣、贏得比賽等都是二項式實驗。

閱讀： Python 中的二項式分佈與實際示例

什麼是二項分佈？

二項分佈可以被稱為衡量在二項式實驗中某事發生或不發生的概率。 一般表示為：

p：特定結果發生的概率

n：我們進行實驗的次數

這裡有一些例子可以幫助你理解，

• 如果我們擲骰子 10 次，那麼 n = 10 和 p 為 1,2,3,4,5 和 6 將是 ⅙。
• 如果我們拋硬幣 15 次，那麼 n = 15，正面和反面的 p 將是 1/2。

有很多與二項分佈相關的術語，可以幫助您找到有關任何問題的有價值的見解。 讓我們看一下二項分佈的兩個主要術語，標準差和均值。

學習世界頂尖大學的數據科學課程。 獲得行政 PG 課程、高級證書課程或碩士課程，以加快您的職業生涯。

二項分佈的標準差

二項分佈的標準差由以下公式確定：

= npq

在哪裡，

n = 試驗次數

p = 成功試驗的概率

q = 1-p = 試驗失敗的概率

二項分佈的平均值

二項分佈的均值由下式確定，

= n*p

在哪裡，

n = 試驗次數

p = 成功試驗的概率

二項式定理簡介

二項式定理可以看作是一種擴展有限冪表達式的方法。 關於二項式展開，您需要記住以下幾點：

• 對於方程 (x+y)n，此展開式中的項數為 n+1。
• 在二項式展開中，兩項的指數之和為 n。
• C0n，C1n，C2n，……。 稱為二項式係數。
• 與起點和終點距離相等的二項式係數總是相等的。

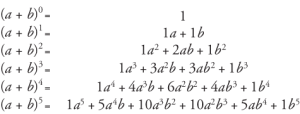
資源

通過查看帕斯卡三角可以找到所有項的係數。

資源

與二項式定理相關的術語

現在讓我們看看二項式定理中最常用的術語。

一般術語

二項式定理中的一般項可以稱為任何給定項的通用方程，如果我們在該方程中插入必要的值，它將對應於該特定項。 它通常表示為 Tr+1。

Tr+1=Crn 。 xn-r 。 年

中期

二項式定理的中項可以稱為二項式定理擴展中的中項值。

如果展開式中的項數為偶數，則第(n/2 + 1)項為中項，若二項式展開式中的項數為奇數，則第[(n+1)/2]項和 [(n+3)/2)th 是中間項。

獨立任期

在表達式的展開中與變量無關的項稱為獨立項。 axp + (b/xq)]n 展開式中的獨立項是

Tr+1 = nCr an-r br，其中 r = (np/p+q) ，它是一個整數。

二項式定理的性質

1. C0 + C1 + C2 + … + Cn = 2n
2. C0 + C2 + C4 + … = C1 + C3 + C5 + … = 2n-1
3. C0 – C1 + C2 – C3 + … +(−1)n 。 nCn = 0
4. nC1 + 2.nC2 + 3.nC3 + … + n.nCn = n.2n-1
5. C1 - 2C2 + 3C3 - 4C4 + … +(-1)n-1 Cn = 0，n > 1
6. C02 + C12 + C22 + …Cn2 = [(2n)!/ (n!)2]

結論

二項式定理是數學中最常用的公式之一。 它在統計學中具有最重要的用途之一，用於解決數據科學中的問題。

查看upGrad與頂尖大學和行業領導者聯合提供的課程。 upGrad 提供的一些課程包括：

PG 數據科學文憑：這是由 upGrad 與 IIIT-B 聯合提供的為期 12 個月的數據科學課程。

數據科學理學碩士：由 upGrad 與 IIIT-B 和利物浦約翰摩爾斯大學聯合提供的為期 18 個月的課程。

數據科學 PG 認證：由 upGrad 與 IIIT-B 聯合提供的為期 7 個月的數據科學課程。

商業分析認證計劃：由 upGrad 提供的為期 3 個月的數據科學和商業分析入門課程，是該領域最好的入門級課程之一。