Binomialsatz: Standardabweichung, verwandte Begriffe und Eigenschaften

Der Binomialsatz ist eine der am häufigsten verwendeten Gleichungen im Bereich der Mathematik und hat auch eine Vielzahl von Anwendungen in verschiedenen anderen Bereichen. Einige der realen Anwendungen des Binomialsatzes umfassen:

• Die Verteilung von IP-Adressen an die Computer.
• Vorhersage verschiedener Faktoren im Zusammenhang mit der Wirtschaft der Nation.
• Wettervorhersage.
• Die Architektur.

Der Binomialsatz, manchmal auch als Binomialerweiterung bekannt, wird in Statistik, Algebra, Wahrscheinlichkeit und verschiedenen anderen Bereichen der Mathematik und Physik verwendet. Der Binomialsatz wird durch die folgende Formel bezeichnet:

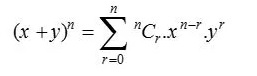
wo, n N und x, y R

Quelle

Was ist ein binomiales Experiment?

Die Formel des Binomialsatzes wird im Allgemeinen zur Berechnung der Wahrscheinlichkeit des Ergebnisses eines Binomialexperiments verwendet. Ein binomiales Experiment ist ein Ereignis, das nur zwei Ergebnisse haben kann. Zum Beispiel Regen an einem bestimmten Tag vorhersagen; das Ergebnis kann nur einer der beiden Fälle sein – entweder es regnet an diesem Tag oder es regnet an diesem Tag nicht.

Da eine Situation nur zwei feste Ergebnisse hat, spricht man von einem binomialen Experiment. In Ihrem täglichen Leben finden Sie viele Beispiele für Binomialexperimente. Das Werfen einer Münze, das Gewinnen eines Rennens usw. sind binomiale Experimente.

Lesen Sie: Binomialverteilung in Python mit Beispielen aus der Praxis

Was ist eine Binomialverteilung?

Die Binomialverteilung kann als Maß für die Wahrscheinlichkeit bezeichnet werden, ob in einem Binomialexperiment etwas passiert oder nicht passiert. Es wird allgemein dargestellt als:

p: Die Wahrscheinlichkeit, dass ein bestimmtes Ergebnis eintritt

n: Wie oft wir das Experiment durchführen

Hier sind einige Beispiele, die Ihnen helfen zu verstehen,

• Wenn wir 10 Mal würfeln, dann ist n = 10 und p für 1,2,3,4,5 und 6 ist ⅙.
• Wenn wir eine Münze 15 Mal werfen, dann ist n = 15 und p für Kopf und Zahl ist 1/2.

Es gibt viele Begriffe im Zusammenhang mit der Binomialverteilung, die Ihnen helfen können, wertvolle Erkenntnisse zu jedem Problem zu gewinnen. Betrachten wir die beiden Hauptbegriffe Standardabweichung und Mittelwert der Binomialverteilung.

Lernen Sie Datenwissenschaftskurse von den besten Universitäten der Welt. Verdienen Sie Executive PG-Programme, Advanced Certificate-Programme oder Master-Programme, um Ihre Karriere zu beschleunigen.

Standardabweichung einer Binomialverteilung

Die Standardabweichung einer Binomialverteilung wird durch die folgende Formel bestimmt:

= npq

Woher,

n = Anzahl der Versuche

p = Die Wahrscheinlichkeit eines erfolgreichen Versuchs

q = 1-p = Die Wahrscheinlichkeit eines fehlgeschlagenen Versuchs

Mittelwert einer Binomialverteilung

Der Mittelwert einer Binomialverteilung wird bestimmt durch:

= n*p

Woher,

n = Anzahl der Versuche

p = Die Wahrscheinlichkeit eines erfolgreichen Versuchs

Einführung in den Binomialsatz

Der Binomialsatz kann als Methode zur Erweiterung eines endlichen Potenzausdrucks angesehen werden. Es gibt ein paar Dinge, die Sie bei einer Binomialerweiterung beachten müssen:

• Für eine Gleichung (x+y)n ist die Anzahl der Terme in dieser Erweiterung n+1.
• Bei der Binomialentwicklung ist die Summe der Exponenten beider Terme n.
• C0n, C1n, C2n, …. heißt Binomialkoeffizient.
• Die von Anfang und Ende gleich weit entfernten Binomialkoeffizienten sind immer gleich.

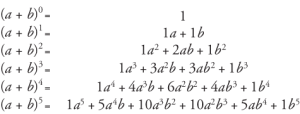
Quelle

Die Koeffizienten aller Terme können gefunden werden, indem man sich das Pascalsche Dreieck ansieht.

Quelle

Begriffe im Zusammenhang mit dem Binomialsatz

Betrachten wir nun die am häufigsten verwendeten Begriffe mit dem Binomialsatz .

Allgemeiner Begriff

Der allgemeine Term im Binomialsatz kann als generische Gleichung für jeden gegebenen Term bezeichnet werden, der diesem spezifischen Term entspricht, wenn wir die erforderlichen Werte in diese Gleichung einfügen. Es wird normalerweise als Tr+1 dargestellt.

Tr+1=Crn . xn-r . Jahr

Mittelfristig

Der Mittelterm des Binomialsatzes kann als der Wert des Mittelterms in der Erweiterung des Binomialsatzes bezeichnet werden.

Wenn die Anzahl der Terme in der Erweiterung gerade ist, ist der (n/2 + 1)-te Term der mittlere Term, und wenn die Anzahl der Terme in der binomialen Erweiterung ungerade ist, dann [(n+1)/2]. und [(n+3)/2)th sind die mittleren Terme.

Unabhängige Laufzeit

Der von den Variablen in der Erweiterung eines Ausdrucks unabhängige Term wird als unabhängiger Term bezeichnet. Der unabhängige Term in der Entwicklung von axp + (b/xq)]n ist

Tr+1 = nCr an-r br, wobei r = (np/p+q) , was eine ganze Zahl ist.

Eigenschaften des Binomialsatzes

1. C0 + C1 + C2 + … + Cn = 2n
2. C0 + C2 + C4 + … = C1 + C3 + C5 + … = 2n-1
3. C0 – C1 + C2 – C3 + … +(−1)n . nCn = 0
4. nC1 + 2.nC2 + 3.nC3 + … + n.nCn = n.2n-1
5. C1 − 2C2 + 3C3 − 4C4 + … +(−1)n-1 Cn = 0 für n > 1
6. C02 + C12 + C22 + …Cn2 = [(2n)!/ (n!)2]

Fazit

Der Binomialsatz ist eine der am häufigsten verwendeten Formeln in der Mathematik. Es hat eine der wichtigsten Anwendungen in der Statistik, die zur Lösung von Problemen in der Datenwissenschaft verwendet wird.

Informieren Sie sich über die Kurse, die upGrad in Zusammenarbeit mit Top-Universitäten und Branchenführern anbietet. Einige der von upGrad angebotenen Kurse sind:

PG-Diplom in Data Science : Dies ist ein 12-monatiger Kurs zu Data Science, der von upGrad in Zusammenarbeit mit IIIT-B angeboten wird.

Master of Science in Data Science : Ein 18-monatiger Kurs, der von upGrad in Zusammenarbeit mit IIIT-B und der Liverpool John Moores University angeboten wird.

PG-Zertifizierung in Data Science : Ein 7-monatiger Kurs zu Data Science, der von upGrad in Zusammenarbeit mit IIIT-B angeboten wird.

Business Analytics-Zertifizierungsprogramm : Ein 3-monatiger Einführungskurs in Data Science und Business Analytics, der von upGrad angeboten wird, ist einer der besten Einstiegskurse in diesem Bereich.