Twierdzenie dwumianowe: odchylenie standardowe, powiązane terminy i właściwości

Twierdzenie dwumianowe jest jednym z najczęściej używanych równań w dziedzinie matematyki, a także ma wiele zastosowań w różnych innych dziedzinach. Niektóre z rzeczywistych zastosowań twierdzenia dwumianowego obejmują:

• Dystrybucja adresów IP do komputerów.
• Przewidywanie różnych czynników związanych z gospodarką narodu.
• Prognoza pogody.
• Architektura.

Twierdzenie dwumianowe, czasami znane również jako rozwinięcie dwumianowe, jest używane w statystyce, algebrze, prawdopodobieństwie i różnych innych dziedzinach matematyki i fizyki. Twierdzenie dwumianowe oznacza poniższy wzór:

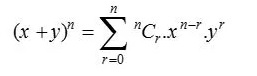
gdzie, n N i x,y R

Źródło

Co to jest eksperyment dwumianowy?

Wzór na twierdzenie dwumianowe jest zwykle używany do obliczania prawdopodobieństwa wyniku eksperymentu dwumianowego. Eksperyment dwumianowy to zdarzenie, które może mieć tylko dwa wyniki. Na przykład przewidywanie deszczu w określonym dniu; rezultatem może być tylko jeden z dwóch przypadków – albo tego dnia będzie padać, albo nie będzie padać tego dnia.

Ponieważ istnieją tylko dwa stałe wyniki sytuacji, nazywa się to eksperymentem dwumianowym. W codziennym życiu możesz znaleźć wiele przykładów eksperymentów dwumianowych. Rzucanie monetą, wygrywanie wyścigu itp. to eksperymenty dwumianowe.

Przeczytaj: Rozkład dwumianowy w Pythonie z przykładami ze świata rzeczywistego

Co to jest rozkład dwumianowy?

Rozkład dwumianowy można określić jako pomiar prawdopodobieństwa, że ​​coś się wydarzy lub nie wydarzy się w eksperymencie dwumianowym. Jest ogólnie przedstawiany jako:

p: prawdopodobieństwo wystąpienia określonego wyniku

n: ile razy wykonujemy eksperyment

Oto kilka przykładów, które pomogą Ci zrozumieć,

• Jeśli rzucimy kostką 10 razy, to n = 10 i p dla 1,2,3,4,5 i 6 będzie .
• Jeśli rzucimy monetą 15 razy, to n = 15, a p dla orłów i reszek wyniesie 1/2.

Istnieje wiele terminów związanych z rozkładem dwumianowym, które mogą pomóc w znalezieniu cennych informacji na temat dowolnego problemu. Przyjrzyjmy się dwóm głównym terminom: odchylenie standardowe i średnia rozkładu dwumianowego.

Ucz się kursów nauki o danych z najlepszych światowych uniwersytetów. Zdobywaj programy Executive PG, Advanced Certificate Programs lub Masters Programs, aby przyspieszyć swoją karierę.

Odchylenie standardowe rozkładu dwumianowego

Odchylenie standardowe rozkładu dwumianowego określa poniższy wzór:

= npq

Gdzie,

n = liczba prób

p = prawdopodobieństwo pomyślnej próby

q = 1-p = Prawdopodobieństwo nieudanej próby

Średnia z rozkładu dwumianowego

Średnia z rozkładu dwumianowego jest określona przez,

= n*p

Gdzie,

n = liczba prób

p = prawdopodobieństwo pomyślnej próby

Wprowadzenie do twierdzenia dwumianowego

Twierdzenie dwumianowe może być postrzegane jako metoda rozwinięcia wyrażenia potęgi skończonej. Jest kilka rzeczy, o których należy pamiętać w przypadku rozwinięcia dwumianowego:

• Dla równania (x+y)n liczba wyrazów w tym rozwinięciu wynosi n+1.
• W rozwinięciu dwumianowym suma wykładników obu wyrazów wynosi n.
• C0n, C1n, C2n, …. nazywa się współczynnikami dwumianowymi.
• Współczynniki dwumianowe znajdujące się w równej odległości od początku i końca są zawsze równe.

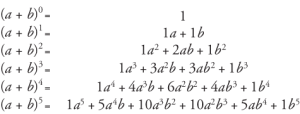
Źródło

Współczynniki wszystkich terminów można znaleźć patrząc na trójkąt Pascala.

Źródło

Pojęcia związane z twierdzeniem dwumianowym

Przyjrzyjmy się teraz najczęściej używanym terminom z twierdzeniem dwumianowym .

Termin ogólny

Termin ogólny w twierdzeniu dwumianowym można nazwać równaniem ogólnym dla dowolnego terminu, który będzie odpowiadał temu konkretnemu terminowi, jeśli wstawimy do tego równania niezbędne wartości. Jest zwykle przedstawiany jako Tr+1.

Tr+1=Crn . xn-r . rok

Średnioterminowy

Składnik środkowy twierdzenia dwumianowego można określić jako wartość składnika środkowego w rozwinięciu twierdzenia dwumianowego.

Jeśli liczba wyrazów w rozwinięciu jest parzysta, (n/2 + 1)-ty wyraz jest wyrazem środkowym, a jeśli liczba wyrazów w rozwinięciu dwumianowym jest nieparzysta, to [(n+1)/2]-ty a [(n+3)/2)th są wyrazami środkowymi.

Niezależny termin

Termin niezależny od zmiennych w rozwinięciu wyrażenia nazywamy terminem niezależnym. Niezależny wyraz w rozwinięciu axp + (b/xq)]n to

Tr+1 = nCr an-r br, gdzie r = (np/p+q) , który jest liczbą całkowitą.

Własności twierdzenia dwumianowego

1. C0 + C1 + C2 + … + Cn = 2n
2. C0 + C2 + C4 + … = C1 + C3 + C5 + … = 2n-1
3. C0 – C1 + C2 – C3 + … +(−1)n . nCn = 0
4. nC1 + 2.nC2 + 3.nC3 + … + n.nCn = n.2n-1
5. C1 − 2C2 + 3C3 − 4C4 + … +(−1)n-1 Cn = 0 dla n > 1
6. C02 + C12 + C22 + …Cn2 = [(2n)!/ (n!)2]

Wniosek

Twierdzenie dwumianowe jest jednym z najczęściej używanych formuł stosowanych w matematyce. Ma jedno z najważniejszych zastosowań w statystyce, które służy do rozwiązywania problemów w data science.

Sprawdź kursy oferowane przez upGrad we współpracy z najlepszymi uniwersytetami i liderami branży. Niektóre z kursów oferowanych przez upGrad to:

PG Diploma in Data Science : Jest to 12-miesięczny kurs na temat Data Science prowadzony przez upGrad we współpracy z IIIT-B.

Masters of Science in Data Science : 18-miesięczny kurs prowadzony przez upGrad we współpracy z IIIT-B i Liverpool John Moores University.

Certyfikacja PG w dziedzinie nauki o danych: 7-miesięczny kurs nauki o danych prowadzony przez upGrad we współpracy z IIIT-B.

Program certyfikacji Business Analytics : 3-miesięczny kurs wprowadzający z nauki o danych i analityki biznesowej prowadzony przez upGrad jest jednym z najlepszych kursów na poziomie podstawowym w tej dziedzinie.