Binom Teoremi: Standart Sapma, İlgili Terimler ve Özellikler

Binom teoremi, matematik alanında en sık kullanılan denklemlerden biridir ve diğer çeşitli alanlarda da çok sayıda uygulaması vardır. Binom teoreminin gerçek dünyadaki uygulamalarından bazıları şunlardır:

• IP Adreslerinin bilgisayarlara dağıtımı.
• Ülke ekonomisi ile ilgili çeşitli faktörlerin tahmini.
• Hava Durumu tahmini.
• Mimari.

Bazen binom açılımı olarak da bilinen binom teoremi, istatistik, cebir, olasılık ve diğer çeşitli matematik ve fizik alanlarında kullanılır. Binom teoremi aşağıdaki formülle gösterilir:

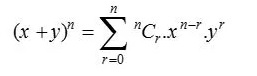
nerede, n N ve x,y R

Kaynak

Binom Deneyi Nedir?

Binom teoremi formülü genellikle bir binom deneyinin sonucunun olasılığını hesaplamak için kullanılır. Binom deneyi, yalnızca iki sonucu olabilen bir olaydır. Örneğin, belirli bir günde yağmur tahmin etmek; sonuç sadece iki durumdan biri olabilir - ya o gün yağmur yağar ya da o gün yağmaz.

Bir durumun yalnızca iki sabit sonucu olduğundan, buna binom deneyi denir. Günlük hayatınızda birçok binom deneyi örneği bulabilirsiniz. Yazı tura atmak, bir yarış kazanmak, vb. iki terimli deneylerdir.

Okuyun: Gerçek Dünya Örnekleriyle Python'da Binom Dağılımı

Binom Dağılım nedir?

Binom dağılımı, bir binom deneyinde bir şeyin olma veya olmama olasılığını ölçmek için adlandırılabilir. Genellikle şu şekilde temsil edilir:

p: Belirli bir sonucun olma olasılığı

n: Deneyi gerçekleştirme sayımız

İşte anlamanıza yardımcı olacak bazı örnekler,

• Zarı 10 kez atarsak, n = 10 ve 1,2,3,4,5 ve 6 için p ⅙ olacaktır.
• 15 kez yazı tura atarsak, n = 15 ve yazı ve tura için p 1/2 olacaktır.

Binom dağılımıyla ilgili, herhangi bir sorun hakkında değerli bilgiler bulmanıza yardımcı olabilecek birçok terim vardır. İki temel terime, standart sapmaya ve binom dağılımının ortalamasına bakalım.

Dünyanın en iyi Üniversitelerinden veri bilimi derslerini öğrenin . Kariyerinizi hızlandırmak için Yönetici PG Programları, Gelişmiş Sertifika Programları veya Yüksek Lisans Programları kazanın.

Binom dağılımının standart sapması

Binom dağılımının standart sapması aşağıdaki formülle belirlenir:

= npq

Neresi,

n = Deneme sayısı

p = Başarılı deneme olasılığı

q = 1-p = Başarısız bir deneme olasılığı

Binom dağılımının ortalaması

Binom dağılımının ortalaması şu şekilde belirlenir:

= n*p

Neresi,

n = Deneme sayısı

p = Başarılı deneme olasılığı

Binom teoremine giriş

Binom teoremi, sonlu bir güç ifadesini genişletmek için bir yöntem olarak görülebilir. Binom açılımı hakkında aklınızda bulundurmanız gereken birkaç şey var:

• Bir (x+y)n denklemi için bu açılımdaki terim sayısı n+1'dir.
• Binom açılımında, her iki terimin üstlerinin toplamı n'dir.
• C0n, C1n, C2n, …. binom katsayıları denir.
• Baştan ve sona eşit uzaklıkta olan binom katsayıları her zaman eşittir.

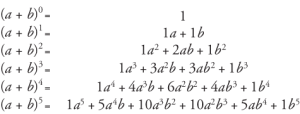
Kaynak

Tüm terimlerin katsayıları Pascal Üçgenine bakılarak bulunabilir.

Kaynak

Binom teoremi ile ilgili terimler

Şimdi binom teoremi ile en sık kullanılan terimlere bakalım .

Genel ifade

Binom teoremindeki genel terim , herhangi bir belirli terim için genel bir denklem olarak adlandırılabilir; bu denkleme gerekli değerleri eklersek, o özel terime karşılık gelir. Genellikle Tr+1 olarak gösterilir.

Tr+1=Krn. xn-r. yıl

Orta vadeli

Binom teoreminin orta terimi, binom teoreminin açılımında orta terimin değeri olarak ifade edilebilir.

Açılımdaki terim sayısı çift ise (n/2 + 1). terim orta terimdir ve iki terimli açılımdaki terim sayısı tek ise [(n+1)/2]. ve [(n+3)/2)'si ortadaki terimlerdir.

Bağımsız Dönem

Bir ifadenin açılımında değişkenlerden bağımsız olan terime bağımsız terim denir. axp + (b/xq)]n'nin açılımındaki bağımsız terim

Tr+1 = nCr an-r br, burada r = (np/p+q) bir tam sayıdır.

Binom Teoreminin Özellikleri

1. C0 + C1 + C2 + … + Cn = 2n
2. C0 + C2 + C4 + … = C1 + C3 + C5 + … = 2n-1
3. C0 – C1 + C2 – C3 + … +(−1)n . nCn = 0
4. nC1 + 2.nC2 + 3.nC3 + … + n.nCn = n.2n-1
5. C1 − 2C2 + 3C3 − 4C4 + … +(−1)n-1 Cn = 0 için n > 1
6. C02 + C12 + C22 + …Cn2 = [(2n)!/ (n!)2]

Çözüm

Binom teoremi, matematikte en çok kullanılan formüllerden biridir. Veri bilimindeki sorunları çözmek için kullanılan istatistikte en önemli kullanımlardan birine sahiptir.

upGrad tarafından en iyi üniversiteler ve endüstri liderleriyle birlikte sağlanan kurslara göz atın. upGrad tarafından sunulan kurslardan bazıları şunlardır:

Veri Biliminde PG Diploması : Bu, upGrad tarafından IIIT-B ile birlikte sağlanan Veri Bilimi üzerine 12 aylık bir kurstur.

Veri Biliminde Yüksek Lisans : UpGrad tarafından IIIT-B ve Liverpool John Moores Üniversitesi ile birlikte sağlanan 18 aylık bir kurs.

Veri Biliminde PG Sertifikasyonu : UpGrad tarafından IIIT-B ile birlikte sağlanan Veri Bilimi üzerine 7 aylık bir kurs.

İş Analitiği Sertifikasyon Programı : upGrad tarafından sağlanan Veri Bilimi ve İş Analitiği üzerine 3 aylık bir giriş kursu, bu alandaki en iyi giriş seviyesi kurslarından biridir.