ทฤษฎีบททวินาม: ส่วนเบี่ยงเบนมาตรฐาน ข้อกำหนดและคุณสมบัติที่เกี่ยวข้อง

ทฤษฎีบททวินามเป็นหนึ่งในสมการที่ใช้บ่อยที่สุดในสาขาคณิตศาสตร์ และยังมีการใช้งานจำนวนมากในสาขาอื่นๆ การประยุกต์ใช้ทฤษฎีบททวินามบางส่วนในโลกแห่งความเป็นจริง ได้แก่:

• การกระจายของที่อยู่ IP ไปยังคอมพิวเตอร์
• การทำนายปัจจัยต่าง ๆ ที่เกี่ยวข้องกับเศรษฐกิจของประเทศ
• การพยากรณ์อากาศ.
• สถาปัตยกรรม.

ทฤษฎีบททวินามหรือบางครั้งเรียกว่าการขยายทวินาม ใช้ในสถิติ พีชคณิต ความน่าจะเป็น และสาขาคณิตศาสตร์และฟิสิกส์อื่นๆ ทฤษฎีบททวินามแสดงโดยสูตรด้านล่าง:

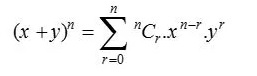
โดยที่ n N และ x,y R

แหล่งที่มา

การทดลองทวินามคืออะไร?

โดยทั่วไป สูตรทฤษฎีบททวินามใช้สำหรับคำนวณความน่าจะเป็นของผลลัพธ์ของการทดลองทวินาม การทดลองทวินามเป็นเหตุการณ์ที่สามารถมีผลลัพธ์ได้เพียงสองอย่างเท่านั้น ตัวอย่างเช่น การพยากรณ์ฝนในวันใดวันหนึ่ง ผลที่ได้คือหนึ่งในสองกรณี – ไม่ว่าฝนจะตกในวันนั้นหรือฝนจะไม่ตกในวันนั้น

เนื่องจากสถานการณ์หนึ่งมีผลคงที่เพียงสองอย่าง จึงเรียกว่าการทดสอบทวินาม คุณสามารถหาตัวอย่างการทดลองทวินามได้มากมายในชีวิตประจำวันของคุณ การโยนเหรียญ ชนะการแข่งขัน ฯลฯ เป็นการทดลองแบบทวินาม

อ่าน: การกระจายทวินามใน Python พร้อมตัวอย่างในโลกแห่งความจริง

การกระจายทวินามคืออะไร?

การแจกแจงทวินามสามารถเรียกได้ว่าวัดความน่าจะเป็นสำหรับบางสิ่งที่จะเกิดขึ้นหรือไม่เกิดขึ้นในการทดลองทวินาม โดยทั่วไปจะแสดงเป็น:

p: ความน่าจะเป็นที่ผลลัพธ์บางอย่างจะเกิดขึ้น

n: จำนวนครั้งที่เราทำการทดลอง

นี่คือตัวอย่างบางส่วนที่จะช่วยให้คุณเข้าใจ

• หากเราทอยลูกเต๋า 10 ครั้ง n = 10 และ p สำหรับ 1,2,3,4,5 และ 6 จะเป็น ⅙
• ถ้าเราโยนเหรียญ 15 ครั้ง n = 15 และ p สำหรับหัวและก้อยจะเป็น 1/2

มีคำศัพท์มากมายที่เกี่ยวข้องกับการแจกแจงแบบทวินาม ซึ่งสามารถช่วยให้คุณพบข้อมูลเชิงลึกอันมีค่าเกี่ยวกับปัญหาใดๆ ลองดูคำศัพท์หลักสองพจน์ ค่าเบี่ยงเบนมาตรฐานและค่าเฉลี่ยของการกระจายทวินาม

เรียนรู้ หลักสูตรวิทยาศาสตร์ข้อมูล จากมหาวิทยาลัยชั้นนำของโลก รับโปรแกรม PG สำหรับผู้บริหาร โปรแกรมประกาศนียบัตรขั้นสูง หรือโปรแกรมปริญญาโท เพื่อติดตามอาชีพของคุณอย่างรวดเร็ว

ส่วนเบี่ยงเบนมาตรฐานของการแจกแจงทวินาม

ค่าเบี่ยงเบนมาตรฐานของการแจกแจงทวินามถูกกำหนดโดยสูตรด้านล่าง:

= npq

ที่ไหน,

n = จำนวนการทดลอง

p = ความน่าจะเป็นของการทดลองที่ประสบความสำเร็จ

q = 1-p = ความน่าจะเป็นของการทดลองที่ล้มเหลว

ค่าเฉลี่ยของการแจกแจงแบบทวินาม

ค่าเฉลี่ยของการแจกแจงแบบทวินามถูกกำหนดโดย

= น*p

ที่ไหน,

n = จำนวนการทดลอง

p = ความน่าจะเป็นของการทดลองที่ประสบความสำเร็จ

บทนำสู่ทฤษฎีบททวินาม

ทฤษฎีบททวินามสามารถเห็นได้ว่าเป็นวิธีการขยายการแสดงออกของกำลังจำกัด มีบางสิ่งที่คุณต้องจำไว้เกี่ยวกับการขยายทวินาม:

• สำหรับสมการ (x+y)n จำนวนพจน์ในการขยายนี้คือ n+1
• ในการขยายทวินาม ผลรวมของเลขชี้กำลังของทั้งสองเทอมคือ n
• C0n, C1n, C2n, …. เรียกว่าสัมประสิทธิ์ทวินาม
• สัมประสิทธิ์ทวินามซึ่งอยู่ห่างจากจุดเริ่มต้นและจุดสิ้นสุดเท่ากันจะเท่ากันเสมอ

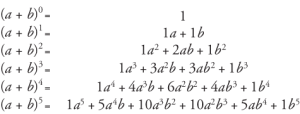
แหล่งที่มา

ค่าสัมประสิทธิ์ของพจน์ทั้งหมดสามารถหาได้โดยดูที่สามเหลี่ยมปาสกาล

แหล่งที่มา

คำศัพท์ที่เกี่ยวข้องกับ ทฤษฎีบททวินาม

ให้เรามาดูคำศัพท์ที่ใช้บ่อยที่สุดกับ ทฤษฎีบท ทวินาม

เทอมทั่วไป

คำศัพท์ทั่วไปใน ทฤษฎีบททวินาม สามารถเรียกได้ว่าเป็นสมการทั่วไปสำหรับเทอมใดๆ ก็ได้ ซึ่งจะสอดคล้องกับคำศัพท์เฉพาะนั้นถ้าเราใส่ค่าที่จำเป็นลงในสมการนั้น โดยปกติจะแสดงเป็น Tr+1

Tr+1=Crn xn-r ปี

เทอมกลาง

เทอมกลางของ ทฤษฎีบททวินาม สามารถเรียกได้ว่าเป็นค่าของเทอมกลางในการขยายตัวของทฤษฎีบททวินาม

หากจำนวนพจน์ในการแผ่ขยายเป็นเลขคู่ พจน์ที่ (n/2 + 1) จะเป็นเทอมกลาง และหากจำนวนพจน์ในการแผ่ขยายทวินามเป็นเลขคี่ ดังนั้น [(n+1)/2]th และ [(n+3)/2)th เป็นเทอมกลาง

เทอมอิสระ

คำที่ไม่ขึ้นกับตัวแปรในการขยายนิพจน์เรียกว่า เทอมอิสระ ศัพท์อิสระในการขยาย axp + (b/xq)]n is

Tr+1 = nCr an-r br โดยที่ r = (np/p+q) ซึ่งเป็นจำนวนเต็ม

คุณสมบัติของทฤษฎีบททวินาม

1. C0 + C1 + C2 + … + Cn = 2n
2. C0 + C2 + C4 + … = C1 + C3 + C5 + … = 2n-1
3. C0 – C1 + C2 – C3 + … +(-1)n . nCn = 0
4. nC1 + 2.nC2 + 3.nC3 + … + n.nCn = n.2n-1
5. C1 − 2C2 + 3C3 − 4C4 + … +(-1)n-1 Cn = 0 สำหรับ n > 1
6. C02 + C12 + C22 + …Cn2 = [(2n)!/ (n!)2]

บทสรุป

ทฤษฎีบททวินามเป็นหนึ่งในสูตรที่ใช้มากที่สุดในวิชาคณิตศาสตร์ มีการใช้งานที่สำคัญที่สุดอย่างหนึ่งในด้านสถิติ ซึ่งใช้ในการแก้ปัญหาด้านวิทยาศาสตร์ข้อมูล

ตรวจสอบหลักสูตรที่จัดทำโดย upGrad ร่วมกับมหาวิทยาลัยชั้นนำและผู้นำในอุตสาหกรรม บางหลักสูตรที่เปิดสอนโดย upGrad ได้แก่:

PG Diploma in Data Science : เป็นหลักสูตร 12 เดือนเกี่ยวกับ Data Science ที่จัดทำโดย upGrad ร่วมกับ IIIT-B

Masters of Science in Data Science : หลักสูตร 18 เดือนโดย upGrad ร่วมกับ IIIT-B และ Liverpool John Moores University

PG Certification in Data Science : หลักสูตร Data Science ระยะยาว 7 เดือนที่จัดทำโดย upGrad ร่วมกับ IIIT-B

โปรแกรมการรับรอง Business Analytics : หลักสูตรเบื้องต้น 3 เดือนเกี่ยวกับ Data Science และ Business Analytics ที่จัดทำโดย upGrad เป็นหนึ่งในหลักสูตรระดับเริ่มต้นที่ดีที่สุดในสาขานี้