نظرية ذات الحدين: الانحراف المعياري ، المصطلحات والخصائص ذات الصلة

نظرية ذات الحدين هي واحدة من المعادلات الأكثر استخدامًا في مجال الرياضيات ولديها أيضًا عدد كبير من التطبيقات في مختلف المجالات الأخرى. تتضمن بعض تطبيقات العالم الحقيقي لنظرية ذات الحدين ما يلي:

• توزيع عناوين IP على أجهزة الكمبيوتر.
• التنبؤ بالعوامل المختلفة المتعلقة باقتصاد الأمة.
• التنبؤ بالطقس.
• بنيان.

تُستخدم نظرية ذات الحدين ، التي تُعرف أحيانًا أيضًا باسم التوسع ذي الحدين ، في الإحصاء والجبر والاحتمال ومختلف مجالات الرياضيات والفيزياء الأخرى. يتم الإشارة إلى نظرية ذات الحدين بالصيغة أدناه:

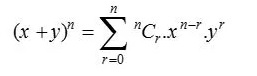
حيث ، n N و x ، y R

مصدر

ما هي التجربة ذات الحدين؟

تُستخدم صيغة نظرية ذات الحدين بشكل عام لحساب احتمالية نتيجة تجربة ذات الحدين. التجربة ذات الحدين هي حدث يمكن أن يكون له نتيجتان فقط. على سبيل المثال ، التنبؤ بالمطر في يوم معين ؛ يمكن أن تكون النتيجة واحدة فقط من الحالتين - إما ستمطر في ذلك اليوم ، أو لن تمطر في ذلك اليوم.

نظرًا لوجود نتيجتين ثابتتين فقط للموقف ، يشار إليها على أنها تجربة ذات الحدين. يمكنك العثور على الكثير من الأمثلة للتجارب ذات الحدين في حياتك اليومية. رمي قطعة نقود ، الفوز في سباق ، إلخ ، هي تجارب ذات حدين.

اقرأ: التوزيع ذي الحدين في بايثون مع أمثلة من العالم الحقيقي

ما هو التوزيع ذو الحدين؟

يمكن تسمية التوزيع ذي الحدين لقياس احتمالية حدوث شيء ما أو عدم حدوثه في تجربة ذات الحدين. يتم تمثيلها بشكل عام على النحو التالي:

ع: احتمال حدوث نتيجة معينة

n: عدد المرات التي نجري فيها التجربة

فيما يلي بعض الأمثلة لمساعدتك على فهم ،

• إذا دحرجنا النرد 10 مرات ، فإن n = 10 و p لـ 1،2،3،4،5 و 6 ستكون ⅙.
• إذا ألقينا قطعة نقود 15 مرة ، فإن n = 15 و p للرؤوس وذيول سيكون 1/2.

هناك الكثير من المصطلحات المتعلقة بالتوزيع ذي الحدين ، والتي يمكن أن تساعدك في العثور على رؤى قيمة حول أي مشكلة. دعونا نلقي نظرة على المصطلحين الرئيسيين ، الانحراف المعياري ومتوسط ​​التوزيع ذي الحدين.

تعلم دورات علوم البيانات من أفضل الجامعات في العالم. اربح برامج PG التنفيذية أو برامج الشهادات المتقدمة أو برامج الماجستير لتتبع حياتك المهنية بشكل سريع.

الانحراف المعياري للتوزيع ذي الحدين

يتم تحديد الانحراف المعياري للتوزيع ذي الحدين بالصيغة أدناه:

= npq

أين،

ن = عدد المحاولات

p = احتمال نجاح التجربة

q = 1-p = احتمال فشل التجربة

متوسط ​​التوزيع ذي الحدين

يتم تحديد متوسط ​​التوزيع ذي الحدين من خلال ،

= ن * ص

أين،

ن = عدد المحاولات

p = احتمال نجاح التجربة

مقدمة في نظرية ذات الحدين

يمكن النظر إلى نظرية ذات الحدين كطريقة لتوسيع تعبير قوة محدود. هناك بعض الأشياء التي يجب أن تضعها في اعتبارك بشأن التوسع ذي الحدين:

• بالنسبة للمعادلة (x + y) n ، فإن عدد الحدود في هذا التوسع هو n + 1.
• في التوسع ذي الحدين ، يكون مجموع الأسس لكلا المصطلحين هو n.
• C0n ، C1n ، C2n ،…. تسمى المعاملات ذات الحدين.
• دائمًا ما تكون المعاملات ذات الحدين التي تكون على مسافة متساوية من البداية والنهاية متساوية.

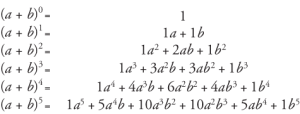
مصدر

يمكن إيجاد معاملات جميع الحدود بالنظر إلى مثلث باسكال.

مصدر

المصطلحات المتعلقة بنظرية ذات الحدين

دعونا الآن نلقي نظرة على المصطلحات الأكثر استخدامًا مع نظرية ذات الحدين .

مصطلح عام

يمكن الإشارة إلى المصطلح العام في نظرية ذات الحدين على أنه معادلة عامة لأي مصطلح معين ، والذي سيتوافق مع هذا المصطلح المحدد إذا أدخلنا القيم الضرورية في تلك المعادلة. وعادة ما يتم تمثيله على أنه Tr + 1.

Tr + 1 = Crn. xn-r. سنة

حد أوسط

يمكن الإشارة إلى المصطلح الأوسط لنظرية ذات الحدين على أنه قيمة الحد الأوسط في توسيع نظرية ذات الحدين.

إذا كان عدد المصطلحات في التوسع زوجيًا ، فإن الحد (n / 2 + 1) هو الحد الأوسط ، وإذا كان عدد المصطلحات في التوسع ذي الحدين فرديًا ، فإن [(n + 1) / 2] th و [(ن + 3) / 2) هما الحد الأوسط.

مصطلح مستقل

المصطلح المستقل عن المتغيرات في توسيع التعبير يسمى المصطلح المستقل. المصطلح المستقل في توسيع axp + (b / xq)] n هو

Tr + 1 = nCr an-r br ، حيث r = (np / p + q) ، وهو عدد صحيح.

خصائص نظرية ذات الحدين

1. C0 + C1 + C2 +… + Cn = 2n
2. C0 + C2 + C4 + ... = C1 + C3 + C5 + ... = 2n-1
3. C0 - C1 + C2 - C3 + ... + (- 1) ن. nCn = 0
4. nC1 + 2.nC2 + 3.nC3 + ... + n.nCn = n.2n-1
5. C1 - 2C2 + 3C3 - 4C4 + ... + (- 1) n-1 Cn = 0 لـ n> 1
6. C02 + C12 + C22 + ... Cn2 = [(2n)! / (n!) 2]

خاتمة

تعد نظرية ذات الحدين واحدة من أكثر الصيغ استخدامًا في الرياضيات. وله أحد أهم الاستخدامات في الإحصاء ، حيث يستخدم في حل المشكلات في علم البيانات.

اطلع على الدورات التي تقدمها upGrad بالتعاون مع أفضل الجامعات وقادة الصناعة. بعض الدورات التي تقدمها upGrad هي:

دبلوم PG في علوم البيانات : هذه دورة مدتها 12 شهرًا في علوم البيانات مقدمة من upGrad بالاشتراك مع IIIT-B.

ماجستير العلوم في علوم البيانات : دورة مدتها 18 شهرًا تقدمها upGrad بالاشتراك مع IIIT-B وجامعة ليفربول جون مورس.

شهادة PG في علوم البيانات : دورة لمدة 7 أشهر في علوم البيانات مقدمة من upGrad بالاشتراك مع IIIT-B.

برنامج شهادة تحليلات الأعمال : دورة تمهيدية مدتها 3 أشهر حول علوم البيانات وتحليلات الأعمال مقدمة من upGrad ، وهي واحدة من أفضل الدورات للمبتدئين في هذا المجال.