Биномиальная теорема: стандартное отклонение, связанные термины и свойства

Биномиальная теорема является одним из наиболее часто используемых уравнений в области математики, а также имеет большое количество приложений в различных других областях. Некоторые из реальных приложений биномиальной теоремы включают:

• Распределение IP-адресов на компьютеры.
• Прогнозирование различных факторов, связанных с экономикой страны.
• Прогноз погоды.
• Архитектура.

Биномиальная теорема, также иногда известная как биномиальное расширение, используется в статистике, алгебре, вероятности и различных других областях математики и физики. Биномиальная теорема обозначается следующей формулой:

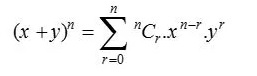
где, n N и x,y R

Источник

Что такое биномиальный эксперимент?

Формула биномиальной теоремы обычно используется для расчета вероятности исхода биномиального эксперимента. Биномиальный эксперимент — это событие, которое может иметь только два исхода. Например, предсказание дождя в определенный день; результатом может быть только один из двух случаев – либо в этот день будет дождь, либо в этот день дождя не будет.

Поскольку в ситуации есть только два фиксированных исхода, такой эксперимент называется биномиальным. Вы можете найти множество примеров биномиальных экспериментов в своей повседневной жизни. Бросание монеты, победа в гонке и т. д. — это биномиальные эксперименты.

Читайте: Биномиальное распределение в Python с реальными примерами

Что такое биномиальное распределение?

Биномиальное распределение можно назвать измерением вероятности того, что что-то произойдет или не произойдет в биномиальном эксперименте. Обычно его представляют в виде:

p: Вероятность того, что произойдет конкретный результат

n: сколько раз мы проводим эксперимент

Вот несколько примеров, которые помогут вам понять,

• Если мы бросим кости 10 раз, то n = 10 и p для 1, 2, 3, 4, 5 и 6 будет ⅙.
• Если мы подбросим монету 15 раз, то n = 15 и p для орла и решки будет 1/2.

Есть много терминов, связанных с биномиальным распределением, которые могут помочь вам найти ценную информацию о любой проблеме. Давайте посмотрим на два основных термина, стандартное отклонение и среднее значение биномиального распределения.

Изучите курсы по науке о данных в лучших университетах мира. Участвуйте в программах Executive PG, Advanced Certificate Programs или Master Programs, чтобы ускорить свою карьеру.

Стандартное отклонение биномиального распределения

Стандартное отклонение биномиального распределения определяется по следующей формуле:

= npq

Где,

n = количество испытаний

p = вероятность успешного испытания

q = 1-p = вероятность неудачного испытания

Среднее значение биномиального распределения

Среднее значение биномиального распределения определяется,

= п * р

Где,

n = количество испытаний

p = вероятность успешного испытания

Введение в биномиальную теорему

Биномиальную теорему можно рассматривать как метод расширения выражения с конечной степенью. Есть несколько вещей, которые вам нужно помнить о биномиальном расширении:

• Для уравнения (x+y)n количество членов в этом разложении равно n+1.
• В биномиальном разложении сумма показателей обоих членов равна n.
• C0n, C1n, C2n, …. называются биномиальными коэффициентами.
• Биномиальные коэффициенты, находящиеся на равном расстоянии от начала и конца, всегда равны.

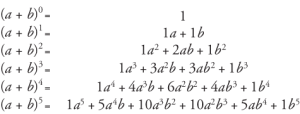
Источник

Коэффициенты всех членов можно найти, взглянув на треугольник Паскаля.

Источник

Термины, связанные с биномиальной теоремой

Давайте теперь посмотрим на наиболее часто используемые термины биномиальной теоремы .

Общий термин

Общий термин в биномиальной теореме можно назвать общим уравнением для любого данного термина, который будет соответствовать этому конкретному термину, если мы вставим в это уравнение необходимые значения. Обычно обозначается как Tr+1.

Тр+1=Крн. хн-р . год

Средний срок

Средний член биномиальной теоремы можно назвать значением среднего члена в расширении биномиальной теоремы.

Если количество членов в разложении четное, то (n/2 + 1)-й член является средним членом, а если количество членов в биномиальном разложении нечетно, то [(n+1)/2]-й и [(n+3)/2)th — средние члены.

Независимый срок

Член, который не зависит от переменных в разложении выражения, называется независимым членом. Независимый член в разложении axp + (b/xq)]n равен

Tr+1 = nCr an-r br, где r = (np/p+q) , что является целым числом.

Свойства биномиальной теоремы

1. С0 + С1 + С2 + … + Сп = 2n
2. С0 + С2 + С4 + … = С1 + С3 + С5 + … = 2n-1
3. C0 – C1 + C2 – C3 + … +(−1)n. nCn = 0
4. nC1 + 2.nC2 + 3.nC3 + … + n.nCn = n.2n-1
5. C1 − 2C2 + 3C3 − 4C4 + … +(−1)n−1 Cn = 0 при n > 1
6. C02 + C12 + C22 + …Cn2 = [(2n)!/ (n!)2]

Заключение

Биномиальная теорема является одной из наиболее часто используемых формул, используемых в математике. Он имеет одно из наиболее важных применений в статистике, которое используется для решения проблем в науке о данных.

Ознакомьтесь с курсами, предлагаемыми upGrad совместно с ведущими университетами и лидерами отрасли. Некоторые из курсов, предлагаемых upGrad:

Диплом PG по науке о данных : это 12-месячный курс по науке о данных, предоставляемый upGrad совместно с IIIT-B.

Магистр наук в области науки о данных : 18-месячный курс, предоставляемый upGrad совместно с IIIT-B и Ливерпульским университетом Джона Мура.

Сертификация PG по науке о данных : 7-месячный курс по науке о данных, предоставляемый upGrad совместно с IIIT-B.

Программа сертификации бизнес-аналитики : 3-месячный вводный курс по науке о данных и бизнес-аналитике, предоставляемый upGrad, является одним из лучших курсов начального уровня в этой области.