二項定理:標準偏差、関連用語およびプロパティ
公開: 2020-09-28二項定理は、数学の分野で最も頻繁に使用される方程式の1つであり、他のさまざまな分野でも多数の用途があります。 二項定理の実際のアプリケーションには、次のものがあります。
- コンピュータへのIPアドレスの配布。
- 国の経済に関連するさまざまな要因の予測。
- 天気予報。
- 建築。
二項定理は、二項式展開とも呼ばれ、統計、代数、確率、およびその他のさまざまな数学および物理学の分野で使用されます。 二項定理は、次の式で表されます。
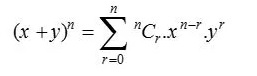
ここで、n Nおよびx、y R
ソース
目次
二項実験とは何ですか?
二項定理の公式は、一般的に二項実験の結果の確率を計算するために使用されます。 二項実験は、2つの結果しか得られないイベントです。 たとえば、特定の日の雨を予測します。 結果は、その日に雨が降るか、その日に雨が降らないかの2つのケースのうちの1つになります。
状況に対する固定された結果は2つしかないため、二項実験と呼ばれます。 日常生活の中で二項実験の例をたくさん見つけることができます。 コインを投げたり、レースに勝ったりすることは、二項実験です。
読む:実際の例を使用したPythonでの二項分布
二項分布とは何ですか?
二項分布は、二項実験で何かが発生する確率または発生しない確率を測定するために呼び出すことができます。 一般的には次のように表されます。
p:特定の結果が発生する確率
n:実験を行った回数
理解に役立ついくつかの例を次に示します。
- サイコロを10回振ると、n = 10となり、1、2、3、4、5、6のpは⅙になります。
- コインを15回投げると、n = 15になり、頭と尾のpは1/2になります。
二項分布に関連する用語はたくさんあり、問題に関する貴重な洞察を見つけるのに役立ちます。 標準偏差と二項分布の平均という2つの主要な項を見てみましょう。
世界のトップ大学からデータサイエンスコースを学びましょう。 エグゼクティブPGプログラム、高度な証明書プログラム、または修士プログラムを取得して、キャリアを早急に進めましょう。
二項分布の標準偏差
二項分布の標準偏差は、次の式で決定されます。
= npq
どこ、
n=試行回数
p=試行が成功する確率
q =1-p=試行が失敗する確率
二項分布の平均
二項分布の平均は、次の式で決定されます。
= n * p
どこ、
n=試行回数
p=試行が成功する確率
二項定理の紹介
二項定理は、有限のべき乗式を拡張する方法と見なすことができます。 二項展開について覚えておく必要のあることがいくつかあります。
- 方程式(x + y)nの場合、この展開の項の数はn+1です。
- 二項式展開では、両方の項の指数の合計はnです。
- C0n、C1n、C2n、…。 二項係数と呼ばれます。
- 開始と終了から等距離にある二項係数は常に等しくなります。
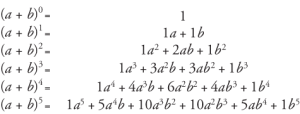

ソース
すべての項の係数は、パスカルの三角形を見るとわかります。
ソース
二項定理に関連する用語
ここで、二項定理で最も頻繁に使用される用語を見てみましょう。
総称
二項定理の一般項は、任意の項の総称方程式と呼ぶことができます。これは、その方程式に必要な値を挿入すると、その特定の項に対応します。 通常、Tr+1として表されます。
Tr + 1=Crn。 xn-r。 年
中期
二項定理の中項は、二項定理の展開における中項の値と呼ぶことができます。
展開の項数が偶数の場合、(n / 2 + 1)番目の項が中間項であり、二項展開の項数が奇数の場合、[(n + 1)/ 2] thおよび[(n + 3)/ 2)thは中間項です。
独立した用語
式の展開で変数から独立している項は、独立項と呼ばれます。 axp +(b / xq)]nの展開における独立項は次のとおりです。
Tr + 1 = nCr an-r br、ここでr =(np / p + q)、これは整数です。
二項定理の性質
- C0 + C1 +C2+…+Cn= 2n
- C0 + C2 +C4+…=C1+ C3 +C5+…=2n-1
- C0 – C1 + C2 – C3 +…+(-1)n。 nCn = 0
- nC1 + 2.nC2 +3.nC3+…+n.nCn= n.2n-1
- C1 − 2C2 + 3C3 − 4C4 +…+(-1)n-1 Cn = 0(n> 1の場合)
- C02 + C12 +C22+…Cn2=[(2n)!/(n!)2]
結論
二項定理は、数学で最もよく使用される式の1つです。 これは、データサイエンスの問題を解決するために使用される、統計における最も重要な用途の1つです。
upGradが一流の大学や業界のリーダーと協力して提供するコースをチェックしてください。 upGradが提供するコースの一部は次のとおりです。
データサイエンスのPGディプロマ:これは、IIIT-Bに関連してupGradが提供するデータサイエンスに関する12か月のコースです。
データサイエンスの理学修士:IIIT-Bおよびリバプールジョンムーア大学と共同でupGradが提供する18か月のコース。
データサイエンスのPG認定:IIIT-Bに関連してupGradが提供するデータサイエンスに関する7か月のコース。
ビジネス分析認定プログラム:upGradが提供するデータサイエンスとビジネス分析に関する3か月の入門コースは、この分野で最高のエントリーレベルのコースの1つです。
統計および確率分析では、二項定理がよく使用されます。 私たちの経済は統計分析と確率分析に大きく依存しているため、これは非常に有益です。 二項定理は、高度な数学とコンピューティングで使用され、より高い累乗の方程式の根を識別します。 また、多くの重要な物理学や数学の方程式を証明するためにも使用されます。 エンジニアリングプロジェクトの天気予報サービス、アーキテクチャ、およびコスト見積もりも、二項定理を使用します。 パスカルの三角形は、二項展開で現れる係数を計算するための代数的アプローチの図ベースの代替手段です。 これは、小さな指数で二項展開の係数を決定する簡単な方法です。 二項分布は、単一の試行のベルヌーイ分布です。つまり、nの値が1の場合です。ベルヌーイ試行またはベルヌーイ実験は単一の成功/失敗実験ですが、二項プロセスは一連の結果です。 イベントの1回の試行の結果はベルヌーイの定理によって処理されますが、同じイベントの複数の試行の結果は二項定理によって処理されます。 イベントの結果が1回だけ必要な場合はBernoulliが使用されますが、結果が複数回必要な場合は二項式が使用されます。二項定理は日常生活でどのように機能しますか?
パスカルの三角形は何を意味しますか?
二項分布とベルヌーイ分布に違いはありますか?
